Observing Matter-Antimatter Oscillations

Roy A. Briere

Viewpoint

Observing Matter-Antimatter Oscillations

Department of Physics, Carnegie Mellon University, Pittsburgh, PA 15213, USA

March 5, 2013• Physics 6, 26

D

-mesons are the fourth in a quartet of neutral mesons to be observed oscillating into their antiparticle partners.

Figure caption — **Figure 1:** (a)—(c) show how the charges of the $π$ mesons from the $D^{*}$ and the $D$ decay can be used to tag the $D$ “flavor” ( $D^{0}$ or ${\bar{D}}^{0}$ ) at production and decay. In a right-sign (RS) decay the charges match [see (a)], unlike in wrong-sign (WS) decays, for which there are two possible sources [see (b),(c)]. (d) displays the weak interaction process responsible for $D^{0} - {\bar{D}}^{0}$ oscillations, which involves all three generations of quarks.

While quantum mechanics is by now a well-established theory, it nonetheless still fascinates both newcomers and experts alike with unusual phenomena. The paradox of Schrödinger’s cat and the subtleties of the two-slit interference are timeless classics. Another less-familiar quantum effect, the oscillations of neutral mesons (bound states of a quark and an antiquark), has also intrigued legions of physicists for nearly sixty years [1]. These mesons oscillate back and forth between particle and antiparticle states. The theoretical ideas underlying this behavior involve concepts that are woven deeply into the history of particle physics. In Physical Review Letters, the LHCb Collaboration has now reported [2] the first significant single-measurement observation of oscillations in the neutral $D$ -meson system.

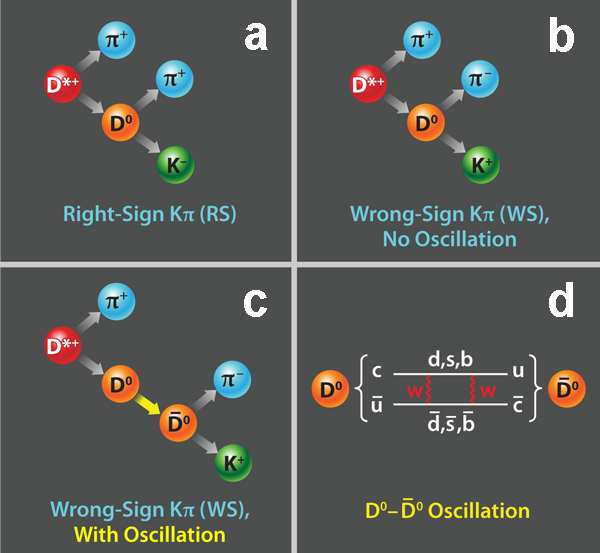
The weak interaction, better known as the fundamental force causing radioactive beta decay, is the alchemist of elementary particle physics; it is able to change the type, or “flavor,” of quarks [quarks can come in the up ( $u$ ), down ( $d$ ), charm ( $c$ ), strange ( $s$ ), top ( $t$ ), or bottom ( $b$ ) flavors]. Recall, for instance, that a neutron, containing one up quark and two down quarks ( $u d d$ ), emits an electron and an antineutrino during beta decay and becomes a proton ( $u u d$ ). Such a flavor change, here from down to up, is a hallmark of the weak interaction. Mesons, built from one quark and one antiquark rather than three quarks, allow for a more subtle possibility. A second-order weak interaction can make the quark and antiquark flavors trade places: a neutral $D^{0} (c \bar{u})$ meson can oscillate into its antiparticle, a ${\bar{D}}^{0} (u \bar{c})$ , as shown in Fig. 1(d). There are four possible meson systems prone to such oscillations. Each of these— $K^{0} (d \bar{s})$ , $D^{0} (c \bar{u})$ , $B^{0} (d \bar{b})$ , and $B_{s}^{0} (s \bar{b})$ , and their respective antiparticles—forms a classic two-state quantum system where oscillations may occur. While oscillations in the $K$ , $B$ , and $B_{s}$ systems have already been established, oscillations between $D^{0}$ and ${\bar{D}}^{0}$ are the last of this quartet to be observed.

Meson oscillations are intimately related to the existence of three generations of quarks: up and down ( $u, d$ ), charm and strange ( $c, s$ ), and top and bottom ( $t, b$ ). Building atoms requires only up and down quarks, yet there are two additional generations. The very existence of these additional quarks is a long-standing mystery in particle physics: they are more massive but otherwise similar copies of the up and down quarks. The quartet of oscillating meson pairs contains these extra quarks, and the detailed physics of the weak interactions gives each of the four meson pairs a somewhat different character.

The character of the oscillations, and hence our strategy to detect them, depends on two key parameters. Weak interactions allow the otherwise degenerate $D^{0}$ and ${\bar{D}}^{0}$ mesons to mix with each other. This results in two new eigenstates, with small differences in their masses and lifetimes, leading to oscillations between $D^{0}$ and ${\bar{D}}^{0}$ with a frequency related to this mass difference. Observations are easier when the oscillation period is comparable to the lifetime. This is the case for the $K$ and $B$ systems, where the phenomenon is now well studied. On the other hand, for the $B_{s}$ system, the oscillations are very fast and experiments required exquisite time resolution to finally resolve them. For the $D$ case, there is little time for the rather slow oscillations to have an effect before the particles decay, and sufficiently high measurement statistics are key to a successful observation.

Searches for $D^{0} - {\bar{D}}^{0}$ oscillations with various techniques recently came to fruition. First evidence came from both the BaBar and Belle Collaborations in 2007, with further proof soon supplied by the CDF Collaboration and other additional measurements [3]. A global combination of these pioneering results established the existence of these oscillations. Now, LHCb has presented [2] the first clear observation based on a single measurement.

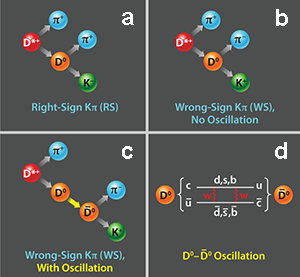
The basic technique used by LHCb involves determining the flavor, $D^{0}$ or ${\bar{D}}^{0}$ , at production and then again at decay, enabling the detection of a flavor change (oscillation). Among the particles produced by the proton-proton collisions studied by LHCb are $D^{*}$ mesons. A $D^{* +}$ commonly decays to $D^{0} π^{+}$ , and a $D^{* -}$ to ${\bar{D}}^{0} π^{-}$ , but never the opposite. Thus the charge of the $π$ meson definitively tags the initial $D$ flavor. To tag at decay, one again uses electric charge in certain specific decays. As shown in Fig. 1(a), one common $D^{0}$ decay yields a $K^{-} π^{+}$ ; in these right-sign (RS) decays, the $π$ from the $D^{*}$ and the $π$ from the $D$ decay have the same sign. A wrong-sign (WS) decay has different $π$ charges and may indicate that a $D^{0} - {\bar{D}}^{0}$ oscillation, followed by the antiparticle decay, ${\bar{D}}^{0} \to K^{+} π^{-}$ , occurred, as shown in Fig. 1(c).

The only fly in the ointment is that a small fraction, about $0.4 %$ , of all decays to $K π$ are actually $D^{0} \to K^{+} π^{-}$ , providing a second source of wrong-sign decays unrelated to oscillations [see Fig. 1(b)]. But time provides us with a fly swatter: this background process has a constant amplitude, while the oscillations vary in time. With no oscillations, the WS/RS rate would be a constant $0.4 %$ vs time. What the LHCb physicists observed instead was a small time-dependent variation ( $\pm 20 %$ ) in the WS/RS rate. To signal oscillation, the wrong-sign decays must come at the right time. The time dependence is fitted to extract the oscillation parameters and the hypothesis that no $D^{0} - {\bar{D}}^{0}$ oscillations occur is ruled out with high statistical confidence ( $9.1$ standard deviations).

Time is crucial to LHCb in another respect. The detector [4] and trigger [5] systems at LHCb are tuned to study states containing bottom or charm quarks. Collisions occur at a rate of $11$ megahertz, but data can only be saved at 3 kilohertz for later analysis. One key to successful selection is the relatively long lifetime, about one picosecond, for states containing these quarks. For fast-moving particles, these short times correspond to measurable propagation distances, which allow for spatially separating them. Since high-precision measurements are required for real-time decisions, an immense amount of work goes into calibration, quality control, maintenance, and other activities necessary to make this process work. The high-quality data obtained for the $D^{0}$ oscillation measurement are a testament to the success of this endeavor. The ability to selectively pick interesting collisions enables a very broad physics program at LHCb [6].

Substantial research efforts are currently dedicated to the weak interactions of quarks and the associated puzzle of their three generations. Ideally, the oscillations discussed here will help in the search for hints of new physics beyond the current standard model of particle physics. It is tantalizing that the experimental results lie toward the upper end of the theoretically predicted range, but unfortunately precise calculations of $D^{0} - {\bar{D}}^{0}$ oscillations are not yet possible. Instead, this and other related experiments stand as a challenge to our theoretical abilities. But even as we wait for progress on that front, we can still savor the subtle harmonies of nature’s oscillating quartet, now finally completed.

References

M. Gell-Mann and A. Pais, “Behavior of Neutral Particles under Charge Conjugation,” Phys. Rev. 97, 1387 (1955)
R. Aaij et al. (LHCb Collaboration), “Observation of $D^{0} - {\bar{D}}^{0}$ Oscillations,” Phys. Rev. Lett. 110, 101802 (2013)
B. Aubert et al. (BaBar Collaboration), “Evidence for $D^{0} - {\bar{D}}^{0}$ Mixing,” Phys. Rev. Lett. 98, 211802 (2007); M. Staric et al. (Belle Collaboration), “Evidence for $D^{0} - {\bar{D}}^{0}$ Mixing,” 98, 211803 (2007); T. Aaltonen et al. (CDF Collaboration), “Evidence for $D^{0} - {\bar{D}}^{0}$ Mixing Using the CDF II Detector,” 100, 121802 (2008)
A. A. Alves, Jr., et al. (LHCb Collaboratio), “The LHCb Detector at the LHC,” J. Inst. 3, S08005 (2008)
R. Aaij et al., “The LHCb Trigger and its Performance,” arXiv:1211.3055
LHCb has already supplied two other Viewpoint topics, one each for $c$ and $b$ physics: see Y. Nir “Charm and Anticharm—Not Quite the Same,” Physics 5, 31 (2012); H. Dreiner, “Mixed Feelings About a Rare Event,” 6, 3 (2013)

About the Author

Roy A. Briere received his Ph.D. in at the University of Chicago and is currently Professor of Physics at Carnegie Mellon University in Pittsburgh. His research focuses on weak interactions of quarks, first strange, then bottom, and currently charm with the CLEO-c and BESIII experiments. He is thankful to Bob Sachs and Bruce Winstein for introducing him to neutral kaon oscillations many years ago. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.