Dissipative Stopwatches

Christine Muschik

Viewpoint

Dissipative Stopwatches

Institute of Photonic Sciences, Av. Carl Friedrich Gauss, 3, 08860 Castelldefels, Barcelona, Spain

March 11, 2013• Physics 6, 29

Contact with the environment usually destroys the delicate operations of a quantum computer, but engineered dissipative processes may allow for a more robust preparation and processing of quantum states.

Figure caption — **Figure 1:** (Top) In conventional time evolution of quantum systems, different input states $| ψ^{in} 〉$ lead to different output states $| ψ^{out} 〉$ if a unitary operation $U$ is applied. (Bottom) Quantum state preparation by reservoir engineering takes a different approach. If the interaction of the system with a bath is engineered such that $| ψ_{fin} 〉$ is the unique steady state of the dissipative process, then the system is driven into this state irrespective of the initial state initiating the evolution paths $ρ_{1}$ , $ρ_{2}$ , etc.

When riffle-shuffling a deck of $52$ cards, seven shuffles are necessary to arrive at a distribution of playing cards that is, to a large degree, independent of the initial ordering. The fact that initial correlations survive if the deck is only shuffled a few times and disappear suddenly after seven shuffles is well known by magicians, who use this phenomenon in card tricks to amaze their audience. In a paper in Physical Review Letters [1], Michael Kastoryano of the Free University of Berlin, Germany, and colleagues show how this effect can be leveraged for quantum information processing.

Quantum information science uses phenomena such as superpositions and entanglement to devise quantum devices capable of performing tasks that cannot be achieved classically. These applications are typically based on unitary dynamics (that is, time evolutions that are governed by the Schrödinger equation). One big practical problem hindering the operation of such devices in the quantum regime is dissipation caused by the interaction of the system with its environment. In the last several years, a new approach to quantum information processing has led to a rethinking of the traditional concepts that rely on unitary dynamics alone and avoid dissipation unconditionally: instead, these new protocols harness dissipative processes for quantum information science.

Actively using dissipation in a controlled way opens up interesting new possibilities and has important advantages: dissipative protocols are robust and, as explained below, allow one to prepare a desired quantum state, irrespective of the initial state of the system. However, the underlying processes are intrinsically probabilistic and time independent. In general, it is therefore not clear how to incorporate them in the existing framework of unitary quantum information processing. One route around this difficulty is to embrace the probabilistic and time-independent nature of these processes and use specifically designed dissipative architectures (see, for example, Ref. [2]), but so far there are very few, and these schemes are conceptually very different from unitary protocols. Protocols based on unitary dynamics typically require precise timing and operations, which are conditioned on previous ones. The work by Kastoryano et al. shows how dissipative processes can be timed and used in a conventional way without losing the specific advantages of dissipative schemes [1].

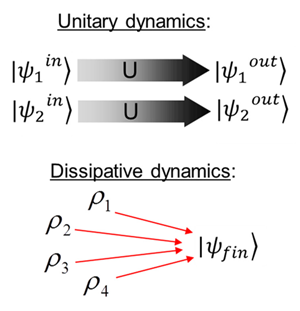
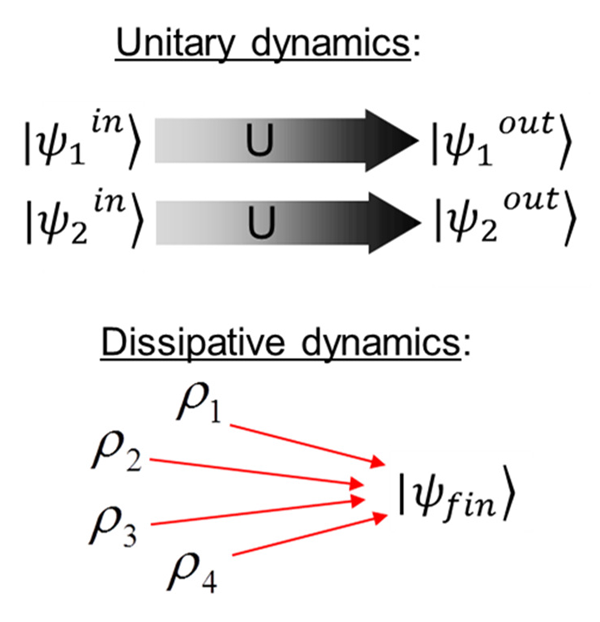
The unitary time evolution (Fig. 1) of a pure quantum state $| ψ 〉$ under a Hamiltonian $\hat{H}$ is governed by the Schrödinger equation $i ħ | \overset{\cdot}{Ψ} (t) 〉 = \hat{H} | Ψ (t) 〉$ . Accordingly, a unitary time evolution $U (t) = e^{- \frac{i \hat{H} t}{ħ}}$ transforms a pure state $| Ψ^{in} 〉$ always into another pure state $| Ψ^{out} 〉 = U (t) | Ψ^{in} 〉$ . Consider, for example, a system with spin states $| ↑ 〉$ and $| ↓ 〉$ . The Hamiltonian $\hat{H} = ħ κ (| g 〉 〈 e | + | g 〉 〈 e |)$ causes the spin to flip. If acting for a time $t = π / 2 κ$ , it transforms $| ↑ 〉$ into $| ↓ 〉$ and $| ↓ 〉$ into $| ↑ 〉$ .

Dissipative processes, in contrast, can turn a pure state into a mixed one that is described by a density matrix $ρ$ , representing a statistical mixture. A dissipative time evolution is governed by a master equation (i.e., an equation of motion for the reduced density operator of a subsystem that interacts with an environment; the dynamics of the system is obtained by tracing out the degrees of freedom of the environment). Here we consider Markov processes (that is, “memoryless” ones) that are described by a time-independent Liouvillian master equation $\overset{\cdot}{ρ} = L (ρ)$ with $L (ρ) = Γ (2 \hat{a} ρ {\hat{a}}^{+} - {\hat{a}}^{+} \hat{a} ρ - ρ {\hat{a}}^{+} \hat{a}$ ), with jump operator $\hat{a}$ and rate $Γ$ . It is instructive to consider, for example, the jump operator $\hat{a} = | ↓ 〉 〈 ↑ |$ . The corresponding master equation causes a system in state $| ↑ 〉$ to relax to $| ↓ 〉$ at a rate $Γ$ . A dissipative process of this type can be understood as applying the jump operator $\hat{a}$ with certain probability $ρ$ , which is determined by $Γ$ . If we prepare our system in state $| ↑ 〉$ and wait a short while, we don’t know whether there has already been a quantum jump $| ↑ 〉 \to | ↓$ ⟩ or not, hence the resulting quantum state is a mixed one $ρ^{mixed} = p | ↓ 〉 〈 ↓ | + (p - 1) | ↑ 〉 〈 ↑ |$ . (The steady state can be still a pure one, $| ↓ 〉$ in this example.) Because of this intrinsically probabilistic feature, dissipative processes are difficult to time. Kastoryano and colleagues develop new tools that allow one to use dissipative processes in such a way that the desired transitions occur at very well-defined points in time (Fig. 2).

The key to dissipative protocols is to tailor the interaction between the system and a bath such that a specific desired jump operator $\hat{a}$ is realized. This jump operator is chosen such that the target state $ρ_{fin}$ is the unique steady state of the dissipative evolution $L (ρ_{fin}) = 0$ . For dissipative quantum computing [3], the result of the calculation is encoded in $ρ_{fin}$ , and if the goal is quantum state engineering, $ρ_{fin}$ can be, for example, an entangled [4] or topological state [5].

This state is reached regardless of the initial state of the system. Should the system be disturbed, the dissipative dynamics will bring it back to the steady state $ρ_{fin}$ . This is impossible for unitary dynamics. In the unitary case, imperfect initialization inevitably leads to deviations from the desired final state. Therefore “reliable state preparation,” the second of the five criteria that DiVincenzo established for a scalable quantum computer [6], was for a long time considered a fundamental requirement for quantum information processing.

Kastoryano et al. extend the toolbox of dissipative quantum information processing by introducing devices for timing this type of process exactly. More specifically, they introduce schemes for (i) preparing a quantum state during a specified time window and (ii) for triggering dissipative operations at specific points in time. The authors use these tools for demonstrating a dissipative version of a one-way quantum computation scheme [7]. The central ingredient that is used here is a very interesting mechanism called the “cutoff phenomenon.” Stochastic processes that have this cutoff quality exhibit a sharp transition in convergence to stationarity. They do not converge smoothly to the stationary distribution during a certain period (if the initial state is far away from the stationary state) but instead converge abruptly (exponentially fast in the system size) at a specific point in time. This behavior was first recognized in classical systems [8]. An intriguing classical example is the shuffling of playing cards outlined above.

This type of mechanism has now been investigated in the quantum setting. In earlier work [9] by some of the authors of the new paper, the cutoff phenomenon is introduced for quantum Markov processes using the notions of quantum information theory. This provides a quantitative tool to study the convergence of quantum dissipative processes. In Ref. [1], Kastoryano et al. employ this quantum-version of the cutoff phenomenon to start and end dissipative processes at specific points in time, thus allowing for the integration in the framework of regular quantum information architectures. In future, these kinds of tools might also become important for new dissipative quantum error correcting schemes and may point towards new insights regarding passive error protection.

Quantum reservoir engineering is a young and rapidly growing area of research. Several protocols have been developed including dissipative schemes for quantum computing [3], quantum state engineering [10], quantum repeaters [2], error correction [11], and quantum memories [12]. Dissipative schemes for quantum simulation [13] and entanglement generation [4] have already been experimentally realized. Actively using dissipative processes is a conceptually interesting direction with important practical advantages. The results presented in Ref. [1] add new tools for exploiting and engineering dissipative processes and provide the linking element for incorporating dissipative methods into the regular framework of quantum information processing.

References

M. J. Kastoryano, M. M. Wolf, and J. Eisert, “Precisely Timing Dissipative Quantum Information Processing,” Phys. Rev. Lett. 110, 110501 (2013)
K. G. H. Vollbrecht, C. A. Muschik, and J. I. Cirac, “Entanglement Distillation by Dissipation and Continuous Quantum Repeaters,” Phys. Rev. Lett. 107, 120502 (2011)
F. Vertraete, M. Wolf, and J. I. Cirac, “Quantum Computation and Quantum-State Engineering Driven by Dissipation,” Nature Phys. 5, 633 (2009)
H. Krauter, C. A. Muschik, K. Jensen, W. Wasilewski, J. M. Petersen, J. Ignacio Cirac, and E. S. Polzik, “Entanglement Generated by Dissipation and Steady State Entanglement of Two Macroscopic Objects,” Phys. Rev. Lett. 107, 080503 (2011)
S. Diehl, E. Rico, M. A. Baranov, and P. Zoller, “Topology by Dissipation in Atomic Quantum Wires,” Nature Phys. 7, 971 (2011)
D. P. DiVincenzo, “The Physical Implementation of Quantum Computation,” Fortschr. Phys. 48, 771 (2000)
R. Raussendorf and H. J. Briegel, “A One-Way Quantum Computer,” Phys. Rev. Lett. 86, 5188 (2003)
P. Diaconis, “The Cutoff Phenomenon in Finite Markov Chains,” Proc. Natl. Acad. Sci. U.S.A. 93, 1659 (1996)
M. J. Kastoryano, D. Reeb, and M. M. Wolf, “A Cutoff Phenomenon for Quantum Markov Chains,” J. Phys. A 45, 075308 (2012)
S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. P. Büchler, and P. Zoller, “Quantum States and Phases in Driven Open Quantum Systems with Cold Atoms,” Nature Phys. 4, 878 (2008)
J. Kerckhoff, H. I. Nurdin, D. S. Pavlichin, and H. Mabuchi, “Designing Quantum Memories with Embedded Control: Photonic Circuits for Autonomous Quantum Error Correction,” Phys. Rev. Lett. 105, 040502 (2010); J. P. Paz and W. H. Zurek, “Continuous Error Correction,” Proc. R. Soc. London A 454, 355 (1998)
F. Pastawski, L. Clemente, and J. Ignacio Cirac, “Quantum Memories Based on Engineered Dissipation,” Phys. Rev. A 83, 012304 (2011)
J. T. Barreiro, M. Müller, P. Schindler, D. Nigg, T. Monz, M. Chwalla, M. Hennrich, C. F. Roos, P. Zoller, and R. Blatt, “An Open-System Quantum Simulator with Trapped Ions,” Nature 470, 486 (2011)

About the Author

Christine Muschik is an Alexander von Humboldt postdoctoral fellow at the Institute of Photonic Sciences (ICFO) in Barcelona, where she joined the quantum optics theory group led by Maciej Lewenstein. She received her Ph.D. at the Max Planck Institute for Quantum Optics, where she worked with Ignacio Cirac in close collaboration with Eugene Polzik at the Niels Bohr Institute. Her thesis on quantum information processing with atoms and photons was completed within the international Ph.D. program of excellence: QCCC (Quantum Computing, Control and Communication) supported by the ENB (Elite Network of Bavaria). Her current research interests are in theoretical quantum optics and quantum nanophotonics.