Mixed Feelings About a Rare Event

Herbert Dreiner

Viewpoint

Mixed Feelings About a Rare Event

Physikalisches Institute, University of Bonn, Nußallee 12, 53115 Bonn, Germany

January 7, 2013• Physics 6, 3

Measurement of a rare-meson decay is an experimental achievement worth celebrating, but so far, no new physics beyond the standard model is indicated.

Figure caption — **Figure 1:** A Feynman diagram represents the decay of a neutral $B$ -meson, $B_{s}^{0}$ , to a pair of muons, $μ^{+} μ^{-}$ . The green sphere on the left indicates the meson, which is a bound state of a strange quark and an antibottom quark. These radiate two $W$ bosons and exchange a top quark in the process. The $W$ bosons fuse to a $Z$ boson, which then produces the two muons in the final state.

One of the most important missions of the Large Hadron Collider at CERN is to search for phenomena that cannot be explained by the standard model of particle physics. In this context, the latest result from the LHCb experiment, now reported in Physical Review Letters, is a bittersweet victory [1]. The LHCb collaboration has, for the first time, observed evidence for the very rare decay of a neutral meson into a pair of muons. Only about one in every $300$ million of the meson’s decays happen this way, and it is no small feat that LHCb has been able to detect the few that do. The rate at which the decay occurs also agrees with the value calculated using the standard model, a theoretical success considering the intricacies involved in the calculations. But many particle physicists were hopeful that the agreement between theory and experiment wouldn’t be quite so good, since a deviation would have been a sign that new physics was at play. So far, no such signs are there, but in the future, the precision of the measurement will improve considerably, potentially allowing smaller deviations from the standard model predictions to be detected.

For all of its successes, the standard model of elementary particle physics has left us with a number of mysteries. In the model, there are six quarks. Three—the up, charm, and top quarks—have electric charge $2 / 3$ ; and three—the down, strange, and bottom quarks—have electric charge $- 1 / 3$ . To this day we have no idea why we have six quarks and not, say, just the two (the up and down quarks) we need to make protons and neutrons, the building blocks of ordinary matter. Another puzzle is the so-called flavor problem: we do not understand why the masses of the six quarks are what they are, or why they vary over several orders of magnitude. The gaps in our knowledge are a bit like having the periodic table without knowing that atoms consist of electrons and nuclei. But this analogy only goes so far: to the best of our knowledge, the quarks are elementary down to a scale of $10^{- 20}$ meters.

One approach to answering our questions is to study particle interactions that involve the outlier quarks, the top and the bottom, since their masses are far greater than the masses of the other quarks. (The bottom quark is, for example, roughly $1000$ times more massive than the down quark.) In the past $15$ years, particle physicists have thus investigated the properties of the bottom quark by measuring the decays of $B$ -mesons, which are bound states between an antibottom quark and another quark. Prior to LHCb, these experiments were led by two $B$ -meson “factories,” one at KEK in Japan, the other at SLAC in California, in addition to the Tevatron at Fermilab.

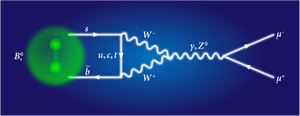
When looking for new physics, the best place to start is where existing theory says an event is not likely to happen: any deviations will be large compared to what we expect. This is why LHCb and the experiments before it have focused on looking for the extremely rare decay of $B_{s}^{0}$ mesons—bound states of a strange quark and an antibottom quark—into a pair of muons (Fig. 1). $B_{s}^{0}$ mesons are electrically neutral and more than $90 %$ of them decay to a $D$ -meson (a meson containing a charm quark) and other particles. But the standard model predicts that a tiny fraction of $B_{s}^{0}$ mesons— $3.23 \pm 0.27 \times 10^{- 9}$ —decay to a pair of muons [2].

Why is this decay so rare? For one, the $B_{s}^{0}$ has zero spin, but because of the standard model interactions that lead to the decay, the muons end up with a total spin of $1$ . To conserve spin angular momentum, one muon must therefore flip its spin, a process suppressed by the size of the muon mass relative to the $B_{s}^{0}$ mass, squared—a factor of about $3 \times 10^{- 4}$ . The second suppressing factor exists because in the $B_{s}^{0}$ decay, a bottom quark and a strange quark annihilate into muons. But a special feature of the standard model is that transitions involving quarks with the same charge—as is the case here—are highly suppressed. (Makoto Kobayashi and Toshihide Maskawa received the 2008 Nobel Prize for their contribution to our understanding this important point.)

Experimentally it is a tremendous challenge to observe such a rare decay. Although the $B$ -factories had a very high luminosity, unlike the LHC, they largely ran below the energy threshold for the production of the $B_{s}^{0}$ meson. The CDF experiment at the Tevatron [3] set the best limits on the meson decay rate before the LHC but could also not reach the new particle accelerator’s sensitivity. Now, LHCb’s measurement shows that the fractional rate of the rare decay [1] is $3 . 2_{- 1.2}^{+ 1.5} \times 10^{- 9}$ . It is one of the rarest decays ever observed and it agrees with the standard model within experimental errors, though these errors, at $40 %$ , are still quite large.

The series of suppression factors given above is peculiar to the structure of the standard model. Since the decay is so rare, even a modest contribution from new physics could easily outshine standard model physics. Leading up to the latest LHCb experiment, hopes were high that experimentalists might observe an anomaly in the decay rate, which could provide hints to a solution to the flavor problem. Now we know that any candidate theory for new physics must predict further contributions to this special decay to be even smaller than what the standard model predicts. As a result, it has been suggested in a BBC News article that the LHCb measurement dealt a “significant blow” to the most widely studied extension of the standard model, supersymmetry. In my view, this is not entirely true, but some background is needed to explain why.

Supersymmetry conjectures that all known particles have a respective “superpartner,” which only differs by half a unit of spin—all other quantum numbers are the same. So, for example, the electron, a fermion, has a superpartner called the scalar electron, or selectron for short. The selectron is the same as the electron in every way except that it has spin zero, and is thus a boson. Furthermore its mass must be larger.

There are many versions of supersymmetry. It turns out that in the “minimal” version of the theory, that is, the one with the fewest number of couplings between particles, the $B$ -meson decay is also suppressed, but because of a different combination of factors than the ones that show up in the standard model calculations. For one, although no spin flip is required, the involved supersymmetric interaction is suppressed by exactly the same factor of muon mass over $B_{s}^{0}$ mass squared. And two, we know from experimental searches for the superpartner particles that, if they exist, they must be much heavier than their standard model counterparts, typically with masses above $1000 GeV / c^{2}$ [4]. In the supersymmetric computation, these particles enter as (heavy) virtual particles, and thus suppress the meson decay. (In Fig. 1, the up, charm and top quarks and the $W$ -bosons are such virtual particles.) The combination of these factors leads to a prediction of the decay rate of the $B$ -mesons into a muon pair that is compatible with the range observed in the experiments [5–8].

What the LHCb measurement has excluded are some other, very well motivated, nonminimal versions of supersymmetry. These versions of the theory don’t feature the special cancellations and would have led to a much higher rate of decay than LHCb observed.

The LHC will soon shut down for a two-year upgrade. Afterwards it will amp up from the $8$ tera-electron-volts (TeV), at which it currently runs, to $14$ TeV, and the luminosity will also be increased. The additional luminosity will lead to an increased production of $B_{s}^{0}$ mesons and thus to a reduction of the experimental error in LHCb’s result by about a factor of $3$ by 2018 [9]. At the still higher luminosities that should be possible at the LHC, LHCb believe they can reduce their error down to about $5 %$ , which is below the current level of the error in theoretical calculations. At this point they will start putting the standard model to a more stringent test.

References

R. Aaij et al. (LHCb Collaboration), “First Evidence for the Decay $B_{s}^{0} \to μ^{+} μ^{-}$ ,” Phys. Rev. Lett. 110, 021801 (2013)
A. J. Buras, J. Girrbach, D. Guadagnoli, and G. Isidori, “On the Standard Model Prediction for $B (B_{s, d} \to μ^{+} μ^{-})$ ,” Eur. Phys. J. C 72, 2172 (2012)
A. Abulencia et al. (CDF Collaboration), “Search for $B_{s}^{0} \to μ^{+} μ^{-}$ and $B_{d}^{0} \to μ^{+} μ^{-}$ Decays in $\bar{p p}$ Collisions with CDF II,” Phys. Rev. Lett. 95, 221805 (2005); “Publisher’s Note: Search for $B_{s}^{0} \to μ^{+} μ^{-}$ and $B_{d}^{0} \to μ^{+} μ^{-}$ Decays in $\bar{p p}$ Collisions with CDF II (Phys. Rev. Lett. 95, 221805 (2005)),” 95, 249905 (2005); T. Aaltonen et al. (CDF Collaboration), “Search for $B_{s}^{0} \to μ^{+} μ^{-}$ and $B^{0} \to μ^{+} μ^{-}$ Decays with CDF II,” 107, 191801 (2011)
S. Heinemeyer, “Still Waiting for Supersymmetry,” Physics 4, 98 (2011)
K. S. Babu and C. Kolda, “Higgs-Mediated $B^{0} \to μ^{+} μ^{-}$ in Minimal Supersymmetry,” Phys. Rev. Lett. 84, 228 (2000)
C. Bobeth, T. Ewerth, F. Krüger, and J. Urban, “Analysis of Neutral Higgs-Boson Contributions to the Decays $B_{s} \to ℓ^{+} ℓ^{-}$ and $\bar{B} \to K ℓ^{+} ℓ^{-}$ ,” Phys. Rev. D 64, 074014 (2001)
P. Bechtle et al., “Constrained Supersymmetry After Two Years of LHC Data: A Global View with Fittino,” J. High Energy Phys. No. 06, 098 (2012)
O. Buchmueller et al., “The CMSSM and NUHM1 in Light of 7 TeV LHC, $B_{s} \to μ^{+} μ^{-}$ and XENON100 Data,” E. Phys. J. C 72, (2012)
R. Aaij et al. (LHCb Collaboration), “Implications of LHCb Measurements and Future Prospects,” arXiv:1208.3355

About the Author

Herbert Dreiner obtained his Ph.D. at the University of Wisconsin, Madison, in 1989. This was followed by postdoctoral work at DESY Hamburg, Oxford University, and ETH Zurich. From 1995 to 2000 he was a senior scientific officer at the Rutherford Laboratories, UK. Since 2000 he has been a professor at Bonn University. His research has mainly focused on searches for physics beyond the standard model at colliders. Since 2002 Herbert has been organizing an extensive outreach effort at Bonn University, the Bonn Physikshow. He was awarded the HEP Outreach Prize of the European Physical Society in 2009.