Antiprotons Reflect a Magnetic Symmetry

Eric R. Hudson; David  Saltzberg

Viewpoint

Antiprotons Reflect a Magnetic Symmetry

Eric R. Hudson

Physics and Astronomy, University of California, Los Angeles, CA 90095, USA

David Saltzberg

March 25, 2013• Physics 6, 36

The ATRAP Collaboration has measured the magnetic moment of the antiproton more precisely than ever before, allowing a new test of

C P T

symmetry.

Figure caption — **Figure 1:** (a) The $C P T$ symmetry can be likened to a mirror that reflects spatial coordinates, flips charge and other additive quantum numbers, and reverses time. To test for cracks in this $C P T$ mirror, physicists check whether the magnetic moment of the proton (left) has the same magnitude as that of the antiproton (right). (Technically, the moments have opposite signs due to the way magnetic moment is defined relative to the spin.) (b) To measure the antiproton’s magnetic moment, the ATRAP Collaboration measures the cyclotron and spin-flip frequencies, $f_{c}$ and $f_{s}$ , respectively. The ratio of these frequencies gives the antiproton’s magnetic moment, $μ_{\bar{p}} = - \frac{f_{s}}{f_{c}} μ_{N}$ , in terms of the nuclear magneton $μ_{N}$ .

Many physical laws are indifferent to distinctions such as left or right and forwards or backwards. On rare occasions, though, a discrepancy shows up, and we say that a symmetry is broken. One symmetry that has so far avoided any signs of breaking is the so-called $C P T$ symmetry, which equates matter and antimatter at a fundamental level. A new test of $C P T$ symmetry involves antiprotons. Specifically, Jack DiSciacca of Harvard University and his colleagues (the ATRAP Collaboration) present the most precise measurement to date of the antiproton magnetic moment [1]. As reported in Physical Review Letters, the results match data on the proton, thus extending $C P T$ ’s shatterproof status for the time being.

Look into a mirror and imagine the world on the other side is not just a reflection, but instead a real physical world. Should nature behave differently in this mirrored world? For decades, most physicists believed the answer was “no.” They assumed that nature was the same in a coordinate system and its mirror image, and they even gave this supposition a name: parity reversal symmetry or $P$ symmetry. However, in 1957, the nuclear physics world was rocked when two back-to-back articles in Physical Review revealed that $P$ symmetry was violated by nature [2,3]. This discovery revolutionized the understanding of the weak interaction.

Further scrutiny revealed that this asymmetry did not act alone. Physicists found that every one of these $P$ -symmetry violations was accompanied by an equal violation of a corresponding symmetry, known as charge-conjugation symmetry or $C$ symmetry, which reverses the signs of a particle’s additive quantum numbers (e.g., its charge, baryon number, etc.). Thus, as long as the mirror not only inverted the space coordinates but also flipped the particle’s additive quantum numbers, physics was the same in the mirrored world. The combined $C P$ symmetry appeared to be a true symmetry of nature, but this view did not last long, as even $C P$ symmetry fell to experiment within a decade [4].

In hindsight, physicists should not have been surprised. No deep principle of physics forbids nature from violating $C$ or $P$ or even $C P$ symmetry. And in the words of the English author T. H. White, “Everything that is not forbidden is compulsory.”

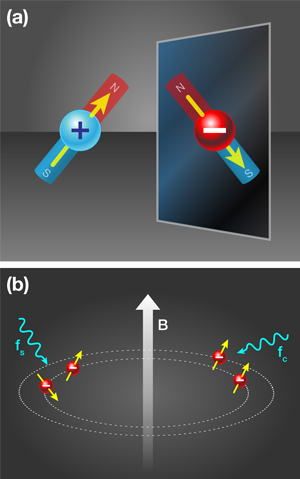
The introduction of a third discrete symmetry, a time-reversal transformation called $T$ , changes the landscape entirely. Now imagine a mirror that not only inverts space and particle quantum numbers but also reverses the arrow of time [see Fig. 1(a)]. Unlike its individual parts, the triple action of $C$ , $P$ , and $T$ is expected to be conserved, since most quantum field theories incorporating Lorentz invariance (i.e., no reference-frame dependence) and locality (i.e., no action-at-a-distance) must respect the combined $C P T$ symmetry absolutely.

Lorentz invariance is a cornerstone of the theory of relativity, therefore if $C P T$ violation is observed it might provide deep insight into the unification of gravity and quantum mechanics. Further, some theories speculate that $C P T$ violation could explain why matter dominates antimatter in our universe. Thus, any experimentally observed $C P T$ violation would be a scientific discovery of the first rank. And since $C P T$ symmetry predicts that particles and their antiparticles should have identical properties, up to a sign, one of the cleanest ways to test $C P T$ symmetry is by comparing matter to antimatter. Thus, physicists have looked for small differences in the mass of protons and antiprotons [5,6]. They have also looked for differences in the lifetime of protons and antiprotons at accelerators and in astrophysical data [7]. However, in all cases, $C P T$ symmetry has withstood these high-precision tests.

The ATRAP Collaboration enters the fray with their own test for $C P T$ violation [1]. They look for a difference in the magnetic moments of the proton and antiproton. To enable this test, they precisely measure the magnetic moment of a single, trapped antiproton, achieving the most sensitive measurement to date of this quantity. They compare their result to the known value of the proton’s magnetic moment and find that the magnitudes are equal within experimental uncertainty, as predicted by the $C P T$ theorem. Though there have been other tests of $C P T$ with better precision overall, the work reported by ATRAP improves the limits on $C P T$ violation in the difference of the proton and antiproton magnetic moments by nearly three orders of magnitude [8].

To make this measurement, the ATRAP collaboration packed up an experimental apparatus originally constructed to measure the proton’s magnetic moment and shipped it to CERN, where antiprotons were available. Conceptually, the measurement protocol they used there is quite simple. A single antiproton is captured from the CERN antiproton beam and trapped in a Penning trap. Classically speaking, the trajectory of the antiproton in the Penning trap is primarily a simple, circular orbit around the magnetic field axis ( $B \approx 5$ tesla). Quantum mechanically speaking, the antiproton’s state is described as $| n, m_{s} 〉$ , where $n$ is the principal quantum number describing the antiproton’s orbit and $m_{s} = \pm 1 / 2$ is the projection of the antiproton’s spin onto the $B$ -field axis. Using nearby antenna electrodes, ATRAP scientists drive both cyclotron transitions, i.e., $| n, m_{s} 〉 \to | n + 1, m_{s} 〉$ , and spin-flip transitions, i.e., $| n, m_{s} 〉 \to | n, m_{s} \pm 1 〉$ , and measure the frequency of both transitions, $f_{c}$ and $f_{s}$ , respectively [see Fig. 1(b)]. The ratio of these two frequencies provides a measure of the $g$ factor of the antiproton: $\frac{f_{s}}{f_{c}} = \frac{g_{\bar{p}}}{2}$ . If we assume the antiproton and proton charge-to-mass ratios are equal (a recent measurement found that they are within $0.1$ parts per billion of each other [6], which constitutes another vote of support for $C P T$ symmetry), then the antiproton magnetic moment can be written as $μ_{\bar{p}} = - \frac{g_{\bar{p}}}{2} μ_{N}$ , where $μ_{N}$ is the nuclear magneton.

Despite the conceptual simplicity of the measurement procedure, the experiment was extremely difficult. Similar experiments with electrons have resolved both the transition between the cyclotron quantum levels and the spin states, but the strength of these signals scales with the magnetic moment of the particle. In the case of antiprotons, the magnetic moment (which is inversely proportional to the mass) is $\sim 2000$ times smaller than that of electrons. Therefore, the ATRAP collaboration had to employ a few tricks to tease out the value of the cyclotron and spin-flip frequencies from the weak experimental signals, which end up being swamped by uncharacterized experimental noise. To circumvent this problem, the ATRAP scientists used a technique, developed for the measurement of the proton’s magnetic moment, which analyzes the character of the experimental noise. They noted that this noise increases whenever a quantum transition occurs, thus allowing them to deduce the frequency at which the transitions occurred.

With this data analysis technique, they determined the antiproton’s magnetic moment to be $\frac{μ_{\bar{p}}}{μ_{N}} = - 2.792 845 (12)$ , which has equal magnitude, within experimental uncertainty, to the NIST CODATA recommended value for the proton magnetic moment of $\frac{μ_{p}}{μ_{N}} = 2.792 847 356 (23)$ . Thus the magnitude of the antiproton and proton magnetic moments differ by less than 5 parts per million, in agreement with the $C P T$ theorem.

If $C P T$ violation did occur it would forever alter our understanding of the universe—or lack thereof! History has taught us that experiments such as this one play an important role in shoring up, or changing, the foundations of physics. So for now, the debate will go on. Will $C P T$ symmetry stand the test of time or will it fall, as did $C$ , $P$ , $C P$ , and most recently $T$ , before it [9]? (See 19 November 2012 Viewpoint). Gerry Gabrielse, the ATRAP spokesperson, was asked this question at a recent lecture, and he replied, “God decides. We measure.”

Correction (25 March 2013): Paragraph 8, sentence 1, “measure the electron’s” changed to “measure the proton’s.” Paragraph 8, sentence 4, ” $B \approx 0.5$ tesla” changed to ” $B \approx 5$ tesla.”

References

J. DiSciacca et al. (ATRAP Collaboration), “One-Particle Measurement of the Antiproton Magnetic Moment,” Phys. Rev. Lett. 110, 130801 (2013)
C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, and R. P. Hudson, “Experimental Test of Parity Conservation in Beta Decay,” Phys. Rev. 105, 1413 (1957)
R. L. Garwin, L. M. Lederman, and M. Weinrich, “Observation of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays: The Magnetic Moment of the Free Muon,” Phys. Rev. 105, 1415 (1957)
J. H. Christenson, J. W. Cronin, V. L. Fitch, and R. Turlay, “Evidence for the $2 π$ Decay of the $K_{2}^{0}$ Meson,” Phys. Rev. Lett. 13, 138 (1964)
M. Hori et al., “Determination of the Antiproton-to-Electron Mass Ratio by Precision Laser Spectroscopy of $\bar{p} {He}^{+}$ ,” Phys. Rev. Lett. 96, 243401 (2006)
G. Gabrielse, A. Khabbaz, D. S. Hall, C. Heimann, H. Kalinowsky, and W. Jhe, “Precision Mass Spectroscopy of the Antiproton and Proton Using Simultaneously Trapped Particles,” Phys. Rev. Lett. 82, 3198 (1999)
J. Beringer et al. (Particle Data Group), “Review of Particle Physics,” Phys. Rev. D 86, 010001 (2012)
T. Pask et al., “Antiproton Magnetic Moment Determined from the HFS of $\bar{p} {He}^{+}$ ,” Phys. Lett. B 678, 55 (2009)
J. P. Lees et al. (The BABAR Collaboration), “Observation of Time-Reversal Violation in the $B^{0}$ Meson System,” Phys. Rev. Lett. 109, 211801 (2012)

About the Authors

Eric Hudson earned his Ph.D. at the University of Colorado Boulder in 2006 for work in atomic, molecular, and optical physics with ultracold polar molecules. After a postdoctoral fellowship at Yale University, he joined the faculty of the University of California, Los Angeles, in 2008. At UCLA his research includes the production and study of ultracold molecular ions, charged-neutral quantum chemical dynamics, new trapped ion qubits, and a search for any variation of the fundamental constants of nature.

David Saltzberg received his Ph.D. from University of Chicago in 1994 for work in particle physics at the Fermilab Tevatron. After a postdoctoral appointment at CERN in Geneva, he joined the faculty of the University of California, Los Angeles, in 1997. His research now includes building new detectors for the Compact Muon Solenoid experiment at the Large Hadron Collider and radio detection of ultrahigh energy cosmic radiation using the polar ice caps.

One-Particle Measurement of the Antiproton Magnetic Moment

J. DiSciacca, M. Marshall, K. Marable, G. Gabrielse, S. Ettenauer, E. Tardiff, R. Kalra, D. W. Fitzakerley, M. C. George, E. A. Hessels, C. H. Storry, M. Weel, D. Grzonka, W. Oelert, and T. Sefzick (ATRAP Collaboration)

Phys. Rev. Lett. 110, 130801 (2013)

Published March 25, 2013

Read PDF