A Fragile Union Between Li and He Atoms

Bretislav Friedrich

Viewpoint

A Fragile Union Between Li and He Atoms

Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin, Germany
The Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA

April 8, 2013• Physics 6, 42

The LiHe van der Waals molecule has been produced and spectroscopically detected and its binding energy found to only suffice to stabilize a single rotationless vibrational state.

Figure caption — **Figure 1:** Dependence of the interatomic potential on distance for the helium-helium, ${He}_{2}$ , and the lithium-helium, $LiHe$ , dimers (full lines, left scale) along with the probability of finding the constituent atoms at a particular interatomic distance, as given by the square of the ground-state vibrational wave function (dashed lines, right scale). Arrows mark the positions of the minima (PM), mean interatomic separations (MIS), as well as the outer turning points (OTP) in the respective potentials. Note that the positions of the minima of the ${He}_{2}$ and $LiHe$ potential-energy curves differ dramatically from the mean interatomic separations. On the scale of the figure, the binding energies of either ${He}_{2}$ or $LiHe$ are within the thickness of the horizontal line marking the dissociation limit. The energy of $1 mK$ is equivalent to $1.381 \times 10^{- 26} J$ .

Neutral atoms or molecules can enter into three types of unions that vastly differ in the strength of the bond between them. While the binding energy of chemically bound atoms is typically on the order of electron volts (eV), hydrogen bonds are about an order of magnitude or two weaker, and van der Waals forces are weaker still. The last arise because of the mutual attraction of electric dipoles carried by, or induced in, atoms or molecules, and their interaction energy is conveniently measured in kelvins (energy divided by Boltzmann’s constant; there are about $10^{4}$ kelvins to an eV). The weakest variety of van der Waals forces—dispersion forces—stem from the mutual induced-dipole–induced-dipole attraction that is indispensable for achieving noble gas cluster formation and condensation [1] but is also prominent in condensed matter systems and in physisorption [2].

First invoked in 1930 by Fritz London, dispersion forces are a necessary consequence of the quantum electron correlations that govern the attraction between atoms or nonpolar molecules at large separations. Proportional to polarizability, London dispersion forces are especially weak for He atoms, which shun entering into unions with other like or unlike atoms as a result [3]. At the same time, the tight binding of helium’s electrons, reflected in high excitation energies and hence a puny polarizability (the smallest of all ground-state atoms), makes the distance of closest approach between helium and other atoms as small as the other atom (or molecule) allows. Thus, of all He atom combinations, it is smallest for the $He - He$ pair. As a result, for ${He}_{2}$ , the London dispersion forces, which vary with the inverse sixth power of the distance, get a chance to loom quite large before being overwhelmed by the repulsive interaction at short range.

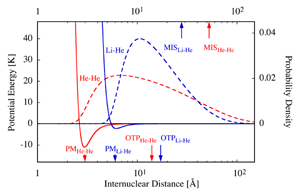
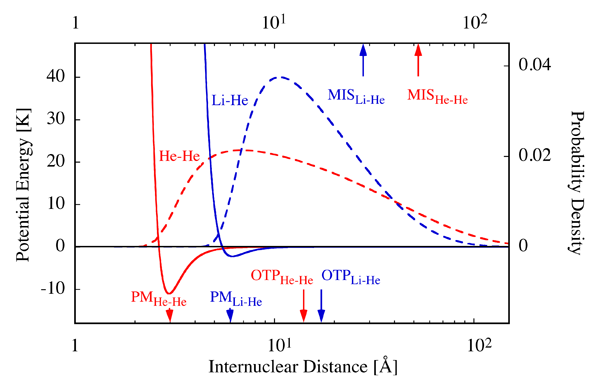
This interplay between attraction and repulsion lends ${He}_{2}$ a fragile single bound state whose energy lies just about $1$ millikelvin (mK) below the dissociation limit [4] (see Fig. 1, also for an energy conversion factor). No wonder then that it took decades to demonstrate the existence of ${He}_{2}$ experimentally. The quest for ${He}_{2}$ culminated in the work of Peter Toennies and Wieland Schöllkopf from the Max Planck Institute in Göttingen, who made use of the matter-wave properties of helium clusters to identify ${He}_{2}$ via diffraction of a helium molecular beam from a transmission grating [5]. It took nearly two more decades to establish experimentally the existence of a second helium-containing diatomic, $LiHe$ , as Naima Tariq and colleagues from the University of Nevada at Reno (UNR) now report in Physical Review Letters [6].

The experimental work by Naima Tariq et al. breaks new ground in several respects: (i) $LiHe$ was prepared via ternary $Li + He + He$ collisions of $Li$ with and within a cryogenic $He$ buffer gas [7]; (ii) $LiHe$ was detected spectroscopically; (iii) the binding energy of $LiHe$ was determined from the measured dependence of the $LiHe$ density on temperature; (iv) $LiHe$ is paramagnetic; (v) $LiHe$ is polar; (vi) according to theory [3,4], $LiHe$ is bound by a potential whose minimum is about $5$ times shallower and its position about $2$ times larger than that of the ${He}_{2}$ potential (see Fig. 1). Below, I will address these distinctive features of the new work in turn.

Instead of relying on molecular beams, the UNR team has implemented the He buffer-gas cooling technique developed and used previously by John Doyle and co-workers at Harvard to study the formation kinetics of van der Waals complexes [8], an effort that has led to indirect evidence for the $AgHe$ dimer [9] and directly inspired the search for the $LiHe$ dimer.

The UNR apparatus consists of a cryostat-cooled cell filled with He buffer gas whose density and temperature can be varied between $10^{17}$ – $10^{18}$ atoms per ${cm}^{3}$ and $1.6$ – $5.0 K$ , respectively. The He density is sufficiently high to ensure thermalization via elastic collisions of the Li atoms produced by pulsed-laser ablation of lithium metal within the cryogenic cell as well as for driving ternary $Li + He + He$ collisions, necessary for the $LiHe$ formation.

A key ingredient of the UNR team’s work is the spectroscopic detection of the fragile $LiHe$ dimer, which possesses excited electronic states (closely related to those of the Li atom) that can be accessed at optical wavelengths (the transition used for the detection of $LiHe$ occurs at $671$ nanometers). Moreover, the position of the last bound vibrational state of the electronically excited state of $LiHe$ that partakes in the optical transition is very weakly bound, which results in a fortuitously strong transition from the ground state (which is also very weakly bound). This, combined with a rapid rate of $LiHe$ formation, affords an abundant fluorescence signal that allowed the UNR experimentalists to obtain a clean high-resolution spectrum. The spectrum revealed that at the temperature of the buffer gas, only a single rovibrational state of $LiHe$ is populated. This state is split, however, into a hyperfine doublet, which arises because of the nuclear spin of the more abundant bosonic isotope of lithium, $^{7} Li$ , used in the experiment. The populations of the hyperfine-doublet states are found to be roughly statistical.

Having established that only a single rovibrational state of LiHe is populated, the UNR team proceeded to determine the state’s binding energy by measuring the temperature dependence of the optically detected $LiHe$ density. The result is a $^{7} {Li}^{4} He$ binding energy of $34 \pm 36 mK$ , consistent with the theoretical prediction of about $6 mK$ . The calculated rotational constant [4] of $40 mK$ precludes the possibility that any higher rotational state than the rotationless ground state could be supported by the only bound vibrational state of $LiHe$ , well in keeping with the experimental findings (the next rotational state would have an energy of $80 mK$ ).

The $LiHe$ dimer is a radical, thanks to the unpaired electron spin of the $Li$ atom, and therefore subject to a sizable Zeeman effect. It is also heteronuclear and therefore polar, although its electric dipole moment is yet to be determined. Both the Zeeman and Stark effects—and their combination—may reveal additional particulars about $LiHe$ ’s structure, dynamics of formation, as well as enable the manipulation of the radical’s translation, including its trapping [10].

One of the most remarkable features of ${He}_{2}$ is its size, as given by the mean separation of the two constituent atoms. This amounts to nearly $50$ angstroms (Å) [4], making ${He}_{2}$ the largest (ground-state) diatomic species. It’s about $70$ -fold the size of the $H_{2}$ molecule. The humungous size of ${He}_{2}$ is caused by its loose bond and by the small mass of $He$ . Although the outer turning point for the zero-point vibration of the dimer occurs at only $14$ Å, the dimer can tunnel its way out through the $1 mK$ barrier imposed by the binding energy. In fact, ${He}_{2}$ spends most of its time—about $80 %$ —in the classically forbidden region beyond the confines of its potential, and is thus a prime example of a halo species [11] (see Fig. 1).

What about $^{7} {Li}^{4} He$ ? Because of its greater binding energy and mass (about $6$ and $1 \frac{1}{2}$ times that of ${He}_{2}$ , respectively), the mean distance between its constituent atoms is down to about $29$ Å [4] (see Fig. 1). It would be down even more, had the position of the minimum of the LiHe potential been the same as for ${He}_{2}$ . It is, however, shifted out to about $6$ Å, twice the ${He}_{2}$ value, because of a less-compact binding of $Li$ ’s electrons and the concomitant predominance of repulsion at correspondingly higher internuclear separations. At the same time, the enhanced $Li$ polarizability makes the London dispersion forces stronger and thereby affords a potential energy well at large internuclear separations, which is deep enough to bind the dimer. As a result, like with ${He}_{2}$ , the bond between $Li$ and $He$ keeps the atoms far apart rather than close. They spend most of their time (over $60 %$ ) in the far out, classically forbidden halo reaches of the potential, beyond the outer turning point of about $17$ Å, where their union is more fragile than elsewhere. The halo behavior is a manifestation of universality [12], as it transcends the specific type of forces involved and can be found, e.g., in nuclear systems.

The ability to produce and detect He dimers within the buffer-gas environment opens the prospect of assembling a whole class of He-containing diatomics and larger clusters, whose properties may be of interest to few- and many-body physics, including the physics of Efimov states [13], which are yet another manifestation of universality. The halo dimers can also be used to study the Casimir retardation effects [14], which arise because of the finite speed of propagation of the electromagnetic field and thereby affect the dispersion forces at large separations. Last but not least, He clusters are of interest to quantum chemistry, whose accuracy is challenged by the fragility of the He bonds.

References

K. T. Tang and J. P. Toennies, “Johannes Diderik van der Waals: A Pioneer in the Molecular Sciences and Nobel Prize Winner in 1910,” Angew. Chem. Int. Ed. 49, 9574 (2009)
B. Friedrich, D. Hoffmann, and J. James, “One Hundred Years of the Fritz Haber Institute,” Angew. Chem. Int. Ed. 50, 10022 (2011)
U. Kleinekathöfer, K. T. Tang, J. P.Toennies, and C. L. Yiu, “Potentials for Some Rare Gas and Alkali-Helium Systems Calculated from the Surface Integral Method,” Chem. Phys. Lett. 249, 257 (1996)
U. Kleinekathöfer, M. Lewerenz, and M. Mladenovic, “Long Range Binding in Alkali-Helium Pairs,” Phys. Rev. Lett. 83, 4717 (1999)
W. Schöllkopf and J. P. Toennies, “Nondestructive Mass Selection of Small van der Waals Clusters,” Science 266, 1345 (1966)
N. Tariq, N. A. Taisan, V. Singh, and J. D. Weinstein, “Spectroscopic Detection of the LiHe Molecule,” Phys. Rev. Lett. 110, 153201 (2013)
H. Suno and B. D. Esry, ”Three-Body Recombination in Cold Helium-Helium-Alkali-Metal-Atom Collisions,” Phys. Rev. A 80, 062702 (2009)
N. Brahms, T. Tscherbul, P. Zhang, J. Klos, R. Forrey, Y. S. Au, H. Sadeghpour, A. Dalgarno, J. M. Doyle, and T. Walker, “Formation and Dynamics of van der Waals Molecules in Buffer-Gas Traps,” Phys. Chem. Chem. Phys. 13, 19125 (2011)
N. Brahms, B. Newman, C. Johnson, T. Greytak, D. Kleppner, and J. Doyle, “Magnetic Trapping of Silver and Copper, and Anomalous Spin Relaxation in the Ag-He System,” Phys. Rev. Lett. 101, 103002 (2008)
B. Friedrich and J. M. Doyle, “Why are Cold Molecules so Hot?,” Chem. Phys. Chem. 10, 604 (2009)
A. S. Jensen, K. Riisager, D. V. Fedorov, and E. Garrido, “Structure and Reactions of Quantum Halos,” Rev. Mod. Phys. 76, 215 (2004)
Ch. H. Greene, “Universal Insights From Few-Body Land,” Phys. Today 63, 40 (2010)
F. Ferlaino and R. Grimm, “Forty Years of Efimov Physics: How a Bizarre Prediction Turned into a Hot Topic,” Physics 3, 9 (2010)
S. K. Lamoreaux, “The Casimir Force: Background, Experiments, and Applications,” Rep. Prog. Phys. 68, 201 (2005)

About the Author

Bretislav Friedrich is Research Group Leader at the Fritz-Haber-Institut der Max-Planck-Gesellschaft, Berlin, Honorary Professor at the Technische Universität Berlin, and Co-Director of the History and Foundations of Quantum Physics Program in Berlin. Among his distinctions is the Outstanding Referee Award of the American Physical Society. He graduated from Charles University, Prague, in 1976, and earned his Ph.D. in chemical physics from the Czech Academy of Sciences in 1981. His experimental and theoretical research at Göttingen (1986–1987), Harvard (1987–2003), and Berlin (since 2003) has dealt with interactions of molecules with fields, cooling and trapping of molecules, collision dynamics, and spectroscopy.