Superconductivity on a Charge Diet

Lu Li

Viewpoint

Superconductivity on a Charge Diet

Department of Physics, University of Michigan, Ann Arbor, MI 48109, USA

April 15, 2013• Physics 6, 45

A study of the thermoelectric properties of the doped insulator, strontium titanate, shows that it superconducts with the lowest charge density ever observed.

Figure caption — **Figure 1:** The Nernst effect occurs when a material is exposed to a temperature gradient and a magnetic field. Mobile charges (referred to as quasiparticles) will tend to move from the warm to the cold side ( $x$ direction), but this motion will induce a force coming from the magnetic field ( $z$ direction). Charge collection in the $y$ direction results in an electric field, constituting the quasiparticle Nernst signal.

For decades researchers have searched for dilute superconductors in insulators and semiconductors. Unlike superconducting metals, in which the charge density is fixed, superconducting semiconductors can be doped with different amounts of carriers, allowing physicists to explore the dependence of superconductivity on carrier density. A well-known example is the doped-band insulator strontium titanate ( ${SrTiO}_{3}$ ). Below its critical temperature of $0.3$ kelvin, it is the most dilute superconductor known. Previous observations have shown that the number of charge carriers in ${SrTiO}_{3}$ —coming from oxygen vacancies or niobium doping—is comparable to the metal bismuth, which has no known superconducting state. New observations, reported in Physical Review X, show that ${SrTiO}_{3}$ superconductivity occurs at even lower carrier densities than previously assumed. As observed in thermoelectric measurements, the superconducting phase occurs in samples doped with one carrier per $10^{5}$ unit cells. This “charge-starved” density is too low to be explained by the conventional superconducting model, the BCS (Bardeen-Cooper-Schrieffer) theory, in which electrons form pairs through a phonon-mediated mechanism.

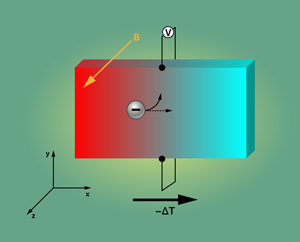
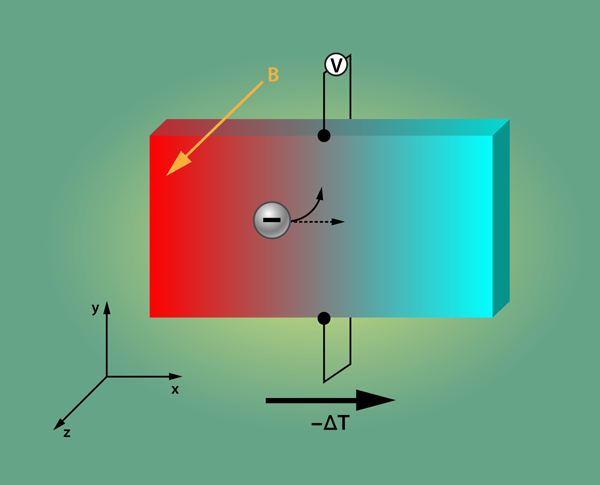
Previous studies have inferred the carrier density of ${SrTiO}_{3}$ by typically using the electrical Hall effect. However, the lower density threshold of the superconducting state has remained an open question. Xiao Lin and colleagues from École Supérieure de Physique et de Chimie Industrielles de la Ville de Paris (ESPCI ParisTech), France, have utilized, for the first time, the Nernst effect to determine the carrier density of annealed $CHEM\textrm{SrTiO}_{3}$ single crystals with very minimal doping [1]. The Nernst effect is a thermoelectric analog of the charge transport Hall effect. It occurs when certain materials are placed under a thermal gradient and a perpendicular magnetic field. The Nernst effect is defined as the resulting transverse electrical field, which can be measured with a voltmeter attached at opposite sides of the material. There are two possible origins of this electric field based on quasiparticles or magnetic vortices [2].

The first case deals with the normal (nonsuperconducting) state in a metal or superconductor, in which the mobile charges, or “quasiparticles,” are either electrons or holes. The quasiparticles follow the temperature gradient direction, say along the $x$ axis, since the entropy flows from the warm end to the cold end (see Fig. 1). A magnetic field pointing in the $z$ direction induces a Lorentz force that will move the quasiparticles sideways, along the $y$ axis. In an open circuit, the charges start to pile up at the $y$ -direction boundary, which induces a transverse balancing electrical field—the Nernst signal. In contrast, the vortex Nernst effect occurs in type-II superconductors, which respond to an external magnetic field with the formation of magnetic vortices, around which the superconducting phase varies by $2 π$ . Under a thermal gradient, these vortices will move from warm to cold just as quasiparticles do in Fig. 1. As one of these vortices passes a line between, say, two electrical leads aligned in the $y$ direction, the superconducting phase along that line will vary in time. Because of the Josephson effect, this evolving phase will generate a voltage in the two leads. The vortex Nernst effect, which shows large amplitude and characteristic field dependence in the superconducting state, is an informative property of the superconducting condensate.

Lin et al. confined themselves to measurements above the critical temperature of ${SrTiO}_{3}$ , meaning the quasiparticle contribution dominated their Nernst signal. The quasiparticle Nernst effect is usually very small. According to the semiclassical approach, the quasiparticle signal is proportional to $d D (ε) / d ε$ , the derivative of the density of states with respect to the chemical potential $ε$ . In most materials, this derivative is small because of a rather smooth electronic density of states. However, in the case of low carrier density and small Fermi surface, the Nernst effect signal can be strongly enhanced, since the density of states has a strong dependence on the chemical potential under these conditions [3]. Furthermore, under intense magnetic field, the orbits of charged particles around the field lines become quantized. This so-called Landau quantization causes a rapid change in the density of states $D (ε)$ as the magnetic field is varied, resulting in oscillations in the Nernst signal.

The researchers observed these magnetic oscillations in the quasiparticle Nernst effect and were thus able to directly resolve the size of the Fermi surface. From this measurement, they were able to precisely nail down the electronic state and carrier density in their ${SrTiO}_{3}$ samples. To their surprise, the superconducting phase exists for carrier densities as low as $5.5$ x $10^{17} {cm}^{- 3}$ , which is almost four orders of magnitude lower than those reported in conventional superconducting semiconductors. The measured carrier density is too small to support the BCS phonon-mediated superconducting state. The BCS theory is based on the fact that an electron will cause a slight deformation in the surrounding crystal lattice, which can attract a second electron to move closer. This trapping leads to a Cooper pair that can move without resistance through the material. However, the electrons in dilute ${SrTiO}_{3}$ are so far away that there is little chance for pair formation through phonons. Therefore these results provide a challenge to theorists trying to explain the origin of superconductivity in ${SrTiO}_{3}$ , a well-known dielectric material with very large dielectric constant ( $\sim 10^{4}$ ) and extremely strong electric screening.

The work is also important given the current research focus on the oxide interface between ${SrTiO}_{3}$ and other oxide insulators such as lanthanum aluminate ( ${LaAlO}_{3}$ ) [4]. The interface between the insulators can be conductive and will even become superconductive below $0.3 kelvin$ , which is the same critical temperature as bulk ${SrTiO}_{3}$ [5]. A magnetic ordering state was discovered to exist and coexist with the superconducting state of the ${LaAlO}_{3} / {SrTiO}_{3}$ interface [6–8]. The superconducting phase can even be tuned with an electric field, which establishes a “domelike” peak in the critical temperature vs doping level, as found in high-temperature superconducting cuprates. To explore these properties further, it will be interesting to measure the Nernst effect for the ${LaAlO}_{3} / {SrTiO}_{3}$ interface. Thanks to its ultrasensitivity to small Fermi surfaces, the Nernst effect may determine if the conductive interface is an ideal two-dimensional system, as was hinted at in previous observations [5].

Furthermore, the Nernst effect can determine if there are strong superconducting fluctuations in the oxide interface system. Lin et al. did not observe any sign of the vortex Nernst signal in bulk ${SrTiO}_{3}$ , but a strong vortex signal might be expected in the interface system, where the two dimensionality may enhance the superconducting fluctuations. In fact, a recent tunneling study discovered that the superconducting gap persists in the under-doped interface state even if the interface turns into an insulator [9]. So far, early tests of the Nernst effect did not spot the superconducting fluctuations in the “optimally doped” ${LaAlO}_{3} / {SrTiO}_{3}$ [10], but future tests are needed for gated under-doped samples. Future experimental work along these lines will hopefully clarify what effect two dimensionality has on the superconducting oxide interface and eventually help pin down the mechanism that allows bulk ${SrTiO}_{3}$ to superconduct with so few charges.

References

X. Lin, Z. Zhu, B. Fauqué, and K. Behnia, “Fermi Surface of the Most Dilute Superconductor,” Phys. Rev. X 3, 021002 (2013)
Y. Wang, L. Li, and N. P. Ong, “Nernst Effect in High- $T_{c}$ superconductors,” Phys. Rev. B 73, 024510 (2006)
K. Benhia, “Nernst Effect and the Boundaries of the Fermi Liquid Picture,” J. Phys. Condens. Matter 21, 113101 (2009)
A. Ohtomo and H. Y. Hwang, “A High-Mobility Electron Gas at the ${LaAlO}_{3} / {SrTiO}_{3}$ Heterointerface,” Nature 427, 423 (2004)
N. Reyren et al., “Superconducting Interfaces Between Insulating Oxides,” Science 317, 1196 (2007)
A. Brinkman, M. Huijben, M. van Zalk, J. Huijben, U. Zeitler J. C. Maan, W. G. van der Wiel, G. Rijnders, D. H. A. Blank, and H. Hilgenkamp, “Magnetic Effects at the Interface Between Non-Magnetic Oxides,” Nature Mater. 6, 493 (2007)
J. Bert, B. Kalisky, C. Bell, M. Kim, Y. Hikita, H. Y. Hwang, and K. A. Moler, “Direct Imaging of the Coexistence of Ferromagnetism and Superconductivity at the ${LaAlO}_{3} / {SrTiO}_{3}$ Interfaces,” Nature Phys. 7, 767 (2011)
L. Li, C. Richter, J. Mannhart, and R. C. Ashoori, “Coexistence of Magnetic Order and Two-Dimensional Super-Conductivity at ${LaAlO}_{3} / {SrTiO}_{3}$ Interfaces,” Nature Phys. 7, 762 (2011)
C. Richter et al., “High-$T_{c}$-Superconductor-like Gap Behavior of a Non-Cuprate 2-D Interface Superconductor,” (to be published)
S. Lerer, M. Ben Shalom, G. Deutscher, and Y. Dagan, “Low-Temperature Dependence of the Thermomagnetic Transport Properties of the ${LaAlO}_{3}$ / ${SrTiO}_{3}$ Interface,” Phys. Rev. B 84, 075423 (2011)

About the Author

Lu Li is an experimental condensed matter physicist interested in quantum correlated materials. He received his Ph.D. from Princeton University in 2008 for work on the Nernst effect and torque magnetometry on unconventional superconductors. He did his postdoctoral work at the Massachusetts Institute of Technology as a Pappalardo fellow, where he studied the capacitance spectroscopy and magnetic state of conductive oxide interfaces. Since 2011 he has been a faculty member of the Department of Physics at the University of Michigan.