The Critical Brain
Neuroscience is at the brink of an unprecedented advance in obtaining instant, detailed maps of neuronal activity during higher brain functions such as object recognition and decision making. These maps will become possible thanks to a rapid cross fertilization among fields (molecular biology, optics, imaging, microfabrication processes, and nanotechnologies) and are considered crucial to make sense of the complex activities that emerge from the billions of neurons making trillions of connections that constitute the human brain. Relevant large-scale research projects are being carried out or are being planned internationally: the Human Connectome Project and BRAIN (Brain Research through Advancing Innovative Neurotechnologies) in the US, the Human Brain Project in Europe, and the Brainnetome project in China. The overarching goal of these large undertakings will be to explain how the brain functions, by acquiring and integrating detailed information on brain structure and its dynamical behavior. But will these endeavors succeed? Knowledge about fine structural details of the brain and observations of neuronal activities may not be sufficient if the emergence of forms of collective behavior is not properly captured. Writing in Physical Review Letters, Ariel Haimovichi, at the University of Buenos Aires in Argentina, and co-workers [1] beautifully exemplify how cooperative phenomena play a key role in determining brain dynamics, by showing that the brain in its resting state (i.e., when not performing an explicit task) is a system at criticality.
Critical systems can be defined as systems that are close to a critical point, generally identified as the boundary of an order-disorder phase transition. Many complex systems far from equilibrium and composed of a large number of interacting elements have been successfully modeled as critical: notable examples range from gene-interaction networks to financial markets. At criticality, these systems can avoid being trapped in one of two extreme cases: a disordered state (when interactions are too weak and the system is dominated by noise) or a globally ordered state in which all elements are locked (when interactions are too strong and the system is completely static). Neither state supports the dualism essential for a complex system like the brain to function: it must maintain some order to ensure coherent functioning (i.e., generate a reproducible behavior in response to a certain stimulus) while allowing for a certain degree of disorder to enable flexibility (i.e., adapt to varying external conditions). Such dualism is instead possible at criticality.
While many degrees of order/disorder are possible, the subtle balance between order and disorder at criticality manifests itself in certain general statistical properties: critical systems exhibit spatial and temporal correlations that are long range (i.e., on scales that are larger than those on which mutual interactions take effect) and follow power-law distributions. Over the last decade, numerous studies have found that the brain at rest exhibits many features typical of a critical state, such as power-law scaling of neuronal avalanches (intermittent outbursts of electrical activity observed in the brain cortex) [2,3], nontrivial long-range spatial and temporal correlations of neuronal activity [4], and anomalous scaling of activity fluctuations with network size [5]. Research carried out in my group has shown that brain networks, by being in the critical state, optimize their response to inputs and maximize their information processing ability [6].
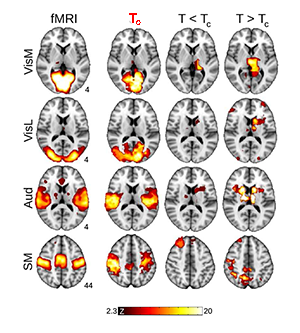
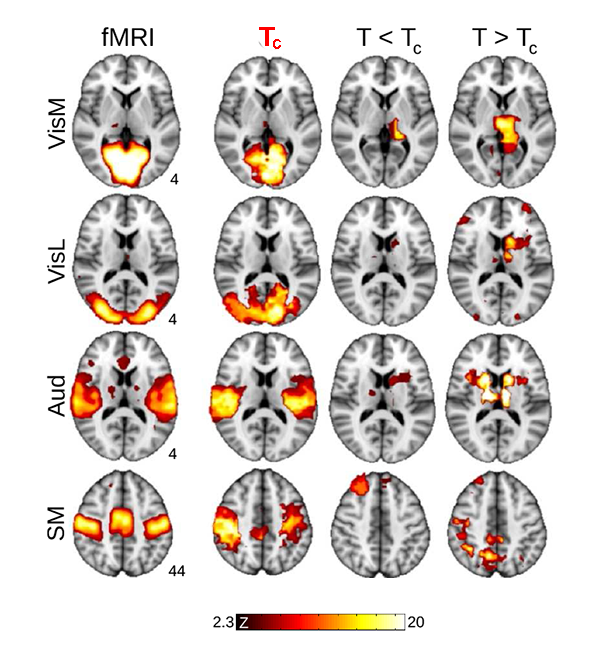
Now, Haimovichi et al. present a simple brain model that, if tuned to criticality, explains the broad range of experimental observations of human brain activity, in particular, reproducing key findings obtained with functional magnetic resonance imaging (fMRI). fMRI, a recent brain imaging technique, indirectly monitors neuronal activities by detecting associated changes in blood flow, measured as a blood-oxygenation-level dependent (BOLD) signal with a spatial resolution of about 1mm3 and temporal resolution of several seconds. Even though neuronal activities are orders of magnitudes faster and much more spatially detailed (down to micrometer scales), fMRI research has been able to deliver an important observation: the human brain at rest exhibits a large-scale spatiotemporal organization into distinct functional networks—so-called resting state networks (RSN) [7]. RSNs are areas of the resting brain—measured in subjects who are not performing any cognitive, language, or motor tasks—in which fluctuations of neural activity are correlated, as revealed by the fact that BOLD signal fluctuations within the same network are synchronous. Each RSN can be related to a specific set of cortical areas associated with certain functions: cognitive, sensory (visual, auditory), and motor RSNs, for instance, have been identified (see Fig. 1).
To model RSN activity, Haimovichi et al. use existing information on how different cortical areas are connected by an underlying network of so-called fiber tracts and apply a charmingly simple three-state model, well known to capture dynamics as diverse as the activity of single neurons or the epidemic spread of infections in populations. In their model, each cortical region, which in the real brain contains hundreds of thousands of neurons, is allowed to be in one of the following three states: quiescent (unexcited, but excitable), excited, or refractory (recently excited and temporarily not excitable). Transitions from the quiescent to the excited state can be spontaneous, or they can be driven if the signals coming from other excited areas add up to exceed a certain threshold. Once excited, the area remains refractory for a short time before it can get excited again.
What the authors found is that such a model can lead to activity clusters similar to those found for RSN activity. But for the model to match the experimental data, the activation threshold had to be set exactly at the level at which their model becomes critical, as illustrated in Fig. 1. At criticality, their model predicts a number of statistical properties that are consistent with experiments: the brain forms activity clusters whose sizes follows a power law with slope of - 3/2, the hallmark of neuronal avalanches [2], corresponding to a peak in the size of the second-largest cluster, as found in percolation models [8]; the correlation length (the distance at which two points in the system behave independently) and its fluctuations diverge and match those seen in human brain data. These results are perfectly in line with an ever-larger body of evidence of neural avalanches gathered from magnetoencephalography measurements [4,9] and from in vitro and in vivo studies of brain activity [3].
An important aspect of this work is the use of detailed structural information on fiber-tracts connectivity to predict global dynamics of the brain. Yet it is worth noting that the data on fiber-tracts connectivity used by the authors are derived from experimental methods [diffusion spectrum or diffusion tensor imaging (DSI/DTI)] that have clear limitations. Such methods underestimate long-range connections and cannot capture the directionality of a fiber tract, which is not consistent with the anatomy of the brain. Future studies will inevitably lead to better fiber-tract modeling that will have to be taken into account. Despite these limitations, the distribution of connectivity weights derived from such methods seems “physiological,” as it has common features with a number of complex systems recently investigated [10].
The authors’ main finding is that structural information and local neuronal dynamics have to be integrated into the framework of criticality to explain brain activity. Since one of the hallmarks of criticality is scale invariance (the property by which similar dynamics/properties are observed at all length scales), their approach might be relevant for different levels of brain organization, ranging from small cortical microcircuits, to cortical columns, to the whole brain, thereby providing a unifying framework for interpreting accumulating information about neuronal structure and dynamics. While in the current study the authors had to fine tune their model to a particular threshold for criticality, a major challenge will be to understand what are the exact physical and biological mechanisms by which the brain arrives at and maintains criticality during learning and development.
References
- A. Haimovici, E. Tagliazucchi, P. Balenzuela, and D. R. Chialvo, “Brain Organization into Resting State Networks Emerges at Criticality on a Model of the Human Connectome,” Phys. Rev. Lett. 110, 178101 (2013)
- J. M. Beggs and D. Plenz, “Neuronal Avalanches in Neocortical Circuits,” J. Neurosci. 23, 11167 (2003)
- D. Plenz, “Neuronal Avalanches and Coherence Potentials,” Eur. Phys. J. Special Topics 205, 259 (2012)
- J. M. Palva, A. Zhigalov, J. Hirvonen, O. Korhonen, K. Linkenkaer-Hansen, and S. Palva, “Neuronal Long-Range Temporal Correlations and Avalanche Dynamics are Correlated with Behavioral Scaling Laws,” Proc. Natl. Acad. Sci. U.S.A. 110, 3585 (2013)
- E. Tagliazucchi, P. Balenzuela, D. Fraiman, and D. R. Chialvo, “Criticality in Large-Scale Brain fMRI Dynamics Unveiled by a Novel Point Process Analysis,” Front. Physiol. 3, (2012)
- W. L. Shew and D. Plenz, “The Functional Benefits of Criticality in the Cortex,” Neuroscientist 19, 88 (2013)
- M. D. Fox and M. E. Raichle, “Spontaneous Fluctuations in Brain Activity Observed with Functional Magnetic Resonance Imaging,” Nature Rev. Neurosci. 8, 700 (2007)
- A. Margolina, H.J. Herrmann, and D. Stauffer, “Size of Largest and Second Largest Cluster in Random Percolation,” Phys. Lett. A 93, 73 (1982)
- O. Shriki, J. Alstott, F. Carver, T. Holroyd, R. N. A. Henson, J. Smith, R. Coppola, E. Bullmore, and D. Plenz “Neuronal Avalanches in the Resting MEG of the Human Brain,” J. Neurosci. 33, 7079 (2013)
- S. Pajevic and D. Plenz, “The Organization of Strong Links in Complex Networks,” Nature Phys. 8, 429 (2012)