Toward Fractional Quantum Hall Physics with Cold Atoms

Maria Daghofer; Masudul Haque

Viewpoint

Toward Fractional Quantum Hall Physics with Cold Atoms

Maria Daghofer

Institute for Theoretical Solid State Physics, IFW Dresden, 01171 Dresden, Germany

Masudul Haque

Max-Planck-Institut für Physik komplexer Systeme, Nothnitzer Straße 38, D-01187 Dresden, Germany

April 29, 2013• Physics 6, 49

Researchers propose new ways to recreate fractional quantum Hall physics using ultracold atoms and molecules.

Figure caption — **Figure 1:** Contrast between the “Landau level” mechanism of realizing FQH states (left column) and the “Chern insulator” mechanism (right column). (a) and (b) show examples of band structures. The traditional mechanism involves Landau levels, each with a Hall conductivity (given by the Chern number C ) of the same sign (a). In Chern-band systems, the bands have different Chern numbers (b). In real space, an effective magnetic flux threads each elementary plaquette (i.e., each little square). In the lattice version of Landau levels, each flux has the same sign (c), just as the effective magnetic field in a trapped rotating Bose gas (e) has the same sign everywhere. In Chern insulators, fluxes often alternate (d), as through a scheme like the one proposed in Ref.[2] using polar molecules in optical lattices (f).

In the fractional quantum Hall (FQH) effect, observed in two-dimensional electron gases in a magnetic field, the resistance transverse to the current flow is quantized to noninteger multiples of $h / e^{2}$ . The fractional values are not an accidental small deviation from the previously observed integer quantum Hall (IQH) effect, but instead point to a type of order that had not been known previously, namely “topological order.” One consequence of topological order is the appearance of fractionalized excitations, which (for example) can carry a charge of $e / 3$ , similar to what is observed in the Hall resistance of the FQH. The idea of topological order with its unconventional properties has since been generalized (e.g., to spin liquids); however, no further experimental realization has been unequivocally established. Now in independent papers in Physical Review Letters, Nigel Cooper and Jean Dalibard [1] and Norman Yao et al. [2] propose to reproduce FQH states with cold atoms and molecules. The proposals differ from earlier ones by building on recent theoretical research, indicating alternative ways to mimic the impact of a magnetic field [3]. Since cold atomic and molecular gases enable experimental tunability far beyond what is possible in solid-state setups, one can hope to customize a variety of FQH-like states.

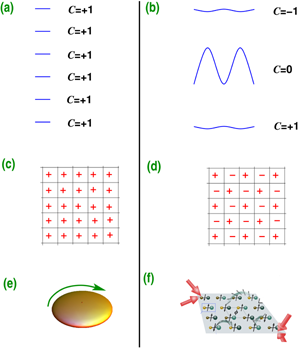
The experimental signature of the FQH and IQH effects are quite similar—step functions in conductance caused by quantized transport in two-dimensional electron gases subject to a magnetic field. In both effects, magnetic fields split the electron energy levels into Landau levels, each consisting of a large number of degenerate single-particle states. The IQH states arise when there are just enough electrons to fill an integer number of Landau levels, while the FQH states appear at fractional fillings. In both effects, topological aspects of the electronic wave functions are important, as the magnetic field also modifies the eigenstates. The Hall conductivity of a filled Landau level turns out to be given by the (first) Chern number, a mathematical concept from the field of topology. This realization allowed the prediction and later realization of topological insulators (TIs), and thus a generalization of IQH physics beyond Landau levels [4]. FQH states are topological in an even stronger sense [5]: Their ground-state degeneracy depends on the topology of the two-dimensional real-space surface they live on, e.g., it is the same for a sphere and a cuboid, but different for a torus.

Topological order violates the long-held belief that ordering requires symmetry breaking. In a magnet, for example, spins are aligned along a common direction chosen spontaneously from originally equivalent ones, thus breaking symmetry. The local magnetization measures how well a spin is aligned and thereby the strength of the order. Topological order, in contrast, does not break any symmetries and has no local order parameter equivalent to the magnetization; it may thus at first sight not appear ordered at all. Instead, it is “nonlocal” and encoded in the wave function of the whole system. Local perturbations can consequently not destroy topological order, which makes such states appealing for fault-tolerant quantum computation.

Unsurprisingly, the goal of realizing FQH physics and topological order in ultracold atoms serving as “quantum simulators” has attracted interest and effort early on. Proposals involved rotating trapped bosonic gases [6], creating effective magnetic fields for lattice bosons [7], or exploiting the internal structure of atomic states to create artificial gauge fields [8]. Yet, despite intense research, the goal of establishing FQH states in cold gases has remained elusive.

The papers by Cooper and Dalibard [1] and by Yao et al. [2] represent a new generation of such proposals. Instead of relying on Landau levels, they build on the above-mentioned generalization of IQH physics to TIs. Even though the Hall conductivity was introduced in the context of magnetic fields, it can be calculated for any filled band in a solid, yielding the Chern number $C$ . It vanishes in most cases, but a band where it is nonzero is said to be “topologically nontrivial,” and a spin-polarized band with $C \neq 0$ is referred to as a “Chern band.” (Similarities and differences between a lattice supporting Landau levels and one supporting Chern bands are sketched in Figure 1.) Accordingly, it was proposed three years ago that Chern bands may provide an alternative route to FQH-like states [3], and substantial interest has been shown in these “fractional Chern insulators” (FCIs). Yet, despite a few materials-based proposals [9], an experimental realization has not been found so far.

In Ref. [2], the authors propose to use polar molecules to realize a bosonic FCI. In this proposal, molecules are strongly bound to their place, but have a rotational degree of freedom. A change in the rotational eigenstate can be seen as a spin flip from the “spin up” ground state, which can in turn be interpreted as a boson. Molecules at neighboring sites can exchange their rotational eigenstates, which allows the boson to hop from site to site. The crucial ingredient is now that the wave function picks up a phase during the hopping process. The phases associated with each bond are distributed in such a way that a boson moving around one of the square plaquettes shown in Fig. 1(d) acquires a phase of $e^{\pm i ϕ}$ , where the fluxes $\pm ϕ$ alternate between plaquettes. This is typical of Chern systems, and the two bands here have indeed Chern numbers $C = \pm 1$ , similar to Fig. 1(b).

The proposal in Ref. [1] also proposes a realization of an FCI system, but is based on earlier ideas by Cooper and collaborators to formulate topological nontrivial models in momentum space. The authors propose to create a periodic spatial modulation of the coupling between lasers and bosonic atoms (such as Rb atoms). Such a modulation creates phases for the hoppings, which in turn again establish the nontrivial band topology in a similar way as a strong magnetic field would.

Since FQH states are driven by interactions between particles, these should be large compared to the kinetic energy. On the other hand, they should be smaller than the gaps between bands, because a mixture of states with $C = 1$ and $C = - 1$ might cancel to topologically trivial $C = 0$ . Fulfilling both criteria is easiest for nearly flat Chern bands, analogous to the high degeneracy of Landau levels. The tunability of cold gases permits this and the optimized band structure given in Ref. [2] has a “flatness ratio” (bandwidth divided by gap to the next band) of $f = 11.5$ , which has been found flat enough for FCI states in other models. The authors consider interacting bosons in this band and find a variety of phases. The FCI competes with superfluid and solid phases, but occupies a sizable region in parameter space. In Ref. [1] the ratio is even better ( $f = 46$ ). By interpolating between this Chern band and a Landau level, the authors provide numerical evidence for several different FCI states at different densities.

Compared to earlier proposals for finding FQH states in cold quantum gases, these two works do not so much propose technological advances but rather extend potential routes to FQH-like states. Building on recent research suggesting that it may not be necessary to copy all features of Landau levels, they propose keeping only some aspects, namely, the Chern number of the band of interest and its reduced dispersion, and omitting others (the Chern numbers of other bands, a constant “magnetic field”). The advantage over materials-based approaches to FCI states is the flexibility of cold gases, which makes it appear more realistic to get into the desired parameter regimes. The experimental realization of an FCI, especially a highly tunable one, would allow study of topological order in far greater depth than the original FQH setting and as a first step would establish whether the proposed generalizations from Landau levels to Chern bands hold true.

References

N. R. Cooper and J. Dalibard, “Reaching Fractional Quantum Hall States with Optical Flux Lattices,” Phys. Rev. Lett. 110, 185301 (2013)
N. Y. Yao, A. V. Gorshkov, C. R. Laumann, A. M. Läuchli, J. Ye, and M. D. Lukin, “Realizing Fractional Chern Insulators in Dipolar Spin Systems,” Phys. Rev. Lett. 110, 185302 (2013)
E. Tang, J-W. Mei, and X-G. Wen, “High-Temperature Fractional Quantum Hall States,” Phys. Rev. Lett. 106, 236802 (2011); T. Neupert, L. Santos, C. Chamon, and C. Mudry, “Fractional Quantum Hall States at Zero Magnetic Field,” 106,236804 (2011); K. Sun, Z. Gu, H. Katsura, and S. Das Sarma, ”Nearly Flatbands with Nontrivial Topology,” 106, 236803 (2011); R. Roy and S. L. Sondhi, “Fractional Quantum Hall Effect without Landau Levels,” Physics 4, 46 (2011)
M. Z. Hasan and C. L. Kane, “Colloquium: Topological Insulators,” Rev. Mod. Phys. 82, 3045 (2010)
X-G. Wen, “Vacuum Degeneracy of Chiral Spin States in Compactified Space,” Phys. Rev. B 40, 7387 (1989); "Mean-Field Theory of Spin-Liquid States with Finite Energy Gap and Topological Orders”, 44, 2664 (1991)
N. R. Cooper, ”Rapidly Rotating Atomic Gases,” Adv. Phys. 57, 539 (2008)
A. S. Sørensen, E. Demler, and M. D. Lukin, “Fractional Quantum Hall States of Atoms in Optical Lattices,” Phys. Rev. Lett. 94, 086803 (2005)
J. Dalibard, F. Gerbier, G. Juzeliunas, and P. Öhberg, “Colloquium: Artificial Gauge Potentials for Neutral Atoms,” Rev. Mod. Phys. 83, 1523 (2011)
D. Xiao, W. Zhu, Y. Ran, N. Nagaosa, and S. Okamoto, “Interface Engineering of Quantum Hall Effects in Digital Transition Metal Oxide Heterostructures,” Nat.Commun. 2, 596 (2011); J. W. Venderbos, S. Kourtis, J. van den Brink, and M. Daghofer, “ Fractional Quantum Hall Liquid Spontaneously Generated by Strongly Correlated $t_{2 g}$ ,” Phys. Rev. Lett. 108,126405 (2012); P. Ghaemi, J. Cayssol, D. N. Sheng, and A. Vishwanath, “Fractional Topological Phases and Broken Time-Reversal Symmetry in Strained Graphene, ” 108, 266801 (2012); Z. Liu, Z.-F. Wang, J.-W. Mei, Y.-S. Wu, and F. Liu, "Flat Chern Band in a Two-Dimensional Organometallic Framework,” 110, 106804 (2013)

About the Authors

Maria Daghofer is a group leader and Emmy-Noether fellow at the Leibniz Institute for Solid-State and Materials Research Dresden, Germany. She obtained her PhD in Graz, Austria, in 2004 and was a postdoc at the Max Planck Institute for Solid State Research (Stuttgart, Germany) and the University of Tennessee (US) before moving to Dresden in 2009. She works on the theory of strongly correlated electron systems, currently focusing on the interplay of correlations and topology.

Masud Haque is a condensed matter theorist at the Max Planck Institute for the Theory of Complex Systems, Dresden, Germany. His research interests are in ultracold atoms, non-equilibrium dynamics, quantum entanglement and topological ordering. His research group currently focuses on quantum many-body systems out of equilibrium.