Simple Structure in Complex Nuclei

John Wood

Viewpoint

Simple Structure in Complex Nuclei

School of Physics, Georgia Institute of Technology, Atlanta, GA 30332, USA

May 6, 2013• Physics 6, 52

Laser spectroscopy of cadmium isotopes confirms the applicability of the nuclear shell model, even for very complex structures.

Figure caption — **Figure 1:** The quadrupole moments, in barns, $b = 10^{- 24} {cm}^{2}$ , of the spin $11 / 2$ state in the odd cadmium isotopes as measured by Yordanov *et al.* The mass number $A$ and neutron number $N$ of the cadmium isotopes (atomic number $Z = 48$ ) are shown on the top and bottom axes, respectively.

Atomic nuclei are finite many-body systems governed by the laws of quantum mechanics. The quest for a thorough understanding of the quantum structure of nuclei is far from finished, even after some seventy years of investigation, because such many-body quantum systems are so complex. In Physical Review Letters, Deyan Yordanov at the Max Planck Institute for Nuclear Physics, Germany, and co-workers report a clever laser spectroscopic study of cadmium isotopes that extends our confidence in one of the fundamental models of nuclear structure while emphasizing some of its surprisingly simple foundations [1]. In contrast to many experiments, their approach yields data in just the form you’d want for testing a model: they measure how a few properties change with a single parameter. This systematic investigation of long sequences of isotopes (constant proton number $Z$ ) or isotones (constant neutron number $N$ ) is a powerful line of enquiry. Such an approach reveals progressive changes in structure with changes of particle number.

Moments, such as magnetic dipole and electric quadrupole, are fundamental properties of finite many-particle quantum systems and they provide very exacting tests of models. Indeed, it was nuclear magnetic moment data available in the 1940s that contributed significantly to the inception of the nuclear shell model [2], and almost contemporaneously, nuclear quadrupole moment data led to the concept of a deformed nucleus [3–6].

Yet nature only furnishes a few hundred (stable) nuclei for experimental study. These are spread over all of the chemical elements, in small groups. But facilities for producing rare isotopes, which are now becoming a major focal point for nuclear physics research, can provide access to long chains ( $30$ or more) of isotopes. These facilities use high-energy protons to spallate (from “to spall” meaning to flake off) nuclei from a heavy element. If the target is heavy, like uranium- $238$ , the process can result in around $1000$ different nuclei. The challenge is then to isolate the nuclear species of interest and deliver them to the experiment.

In the study of Yordanov et al., isotopes of cadmium (atomic number $Z = 48$ ) spanning over twenty mass numbers ( $A = Z + N = 107$ to $129$ ) are isolated, one mass at a time, using a mass separator, and subjected to high-precision optical hyperfine spectroscopy. The production of the cadmium isotopes is by fission of $^{238} U$ using high-energy protons at ISOLDE-CERN.

The authors followed a sequence of ingenious steps to obtain their results. They first directed the high-energy protons onto a tungsten converter to produce large quantities of low-to-medium-energy neutrons that induce fission in the uranium target. While fission still leads to hundreds of different nuclei, they are predominantly neutron-rich, unlike spallation, which yields “everything.” The reaction products were separated by mass number and all combinations of $Z + N$ with a fixed $A$ are delivered to the experimental measurement device. A temperature-controlled quartz transfer line to the ion source selectively transported the cadmium isotopes, retaining isotopes of other chemical, i.e., $Z$ , species until they decayed. The authors then used a laser to ionize the isotopes delivered to the ion source and injected the resulting ion beam into a so-called Paul trap [7]. Ions were intermittently extracted from the trap in short time bunches to enhance the signal-to-background ratio in the optical measurements.

To study the atomic transitions in the cadmium ions, Yordanov et al. used deep-UV laser spectroscopy. To reach the deep-UV, fourth-harmonic generation of visible laser light was used. Essentially, this increased the sensitivity of the technique. (But, as noted by the authors, it also establishes a technique that could provide access to isotopic chains that were heretofore inaccessible.) The atomic spectra of the cadmium ions, recorded for individual masses, have common atomic features but differ in the nuclear magnetic and quadrupole moments that influence the hyperfine structure of the spectra. This permits the extraction of high-precision moment data for each of the cadmium isotopes.

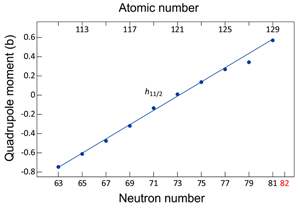
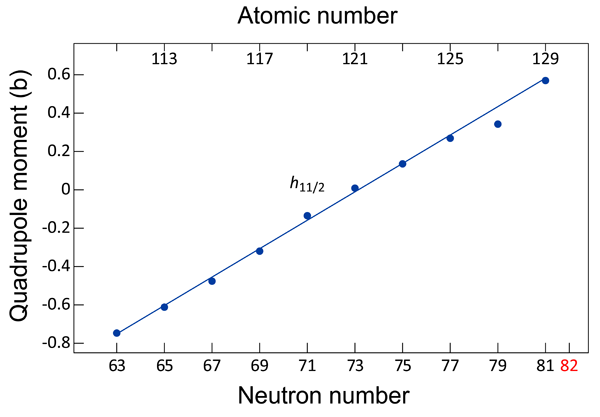
What is remarkable in the results of Yordanov et al. is that for all of the complexity of the isotopes studied, the quadrupole moments of one particular nuclear state exhibit a linear behavior with changing neutron number (Fig. 1). This nuclear state is well defined in the nuclear shell model as a neutron behaving as an independent particle in an orbital with angular momentum $5$ and spin coupled parallel to yield a total spin-orbit value of $11 / 2$ .

The complexity of the structure involved can best be visualized from the perspective that what is changing in the series of isotopes studied is the neutron number. Nevertheless, the unpaired neutron in the “ $11 / 2$ ” state in each of the odd-mass cadmium isotopes behaves in nearly the same way: such behavior was suggested theoretically [8].

Essentially, the simplicity comes from the tendency for like nucleons to pair off and form a so-called “condensate,” very similar to that occurring in superconductors. However, behavior such as that reported by Yordanov et al. was thought only to occur in the extreme situation in which either the protons or the neutrons closed an energy shell and therefore were inactive. In the cadmium isotopes (which do not have a closed proton shell), such simplicity for the neutrons is manifestly surviving.

The result reported by Yordanov et al. is a success for the nuclear shell model and for the concept of pairing of neutrons and of protons to produce a simple and persistent structure in a long isotopic chain. The challenge to the theorists now is to explain this simplicity.

The investigation also illustrates the remarkable control that experimentalists now have over the production and study of difficult to produce isotopes. This structural quest in the exploration of the nuclear landscape is a key motivation for the next major nuclear physics facility in the USA in the form of the Facility for Rare Isotope Beams (FRIB), planned for completion in 2021 at Michigan State University.

References

D. T. Yordanov et al., “Spins, Electromagnetic Moments, and Isomers of $^{107 - 129} C d$ ,” Phys. Rev. Lett. 110, 192501 (2013)
M. Goeppert-Mayer, “Nuclear Configurations in the Spin-Orbit Coupling Model. I. Empirical Evidence,” Phys. Rev. 78, 16 (1950)
A. Bohr, “Rotational Motion in Nuclei,” Rev. Mod. Phys. 48, 365 (1976)
B. Mottelson, “Elementary Modes of Excitation in the Nucleus,” Rev. Mod. Phys. 48, 375 (1976)
J. Rainwater, “Background for the Spheroidal Nuclear Model Proposal,” Rev. Mod. Phys. 48, 385 (1976)
G. Neyens, “Nuclear Magnetic and Quadrupole Moments for Nuclear Structure Research on Exotic Nuclei,” Rep. Prog. Phys. 66, 633 (2003)
W. Paul, “Electromagnetic Traps for Charged and Neutral Particles,” Rev. Mod. Phys. 62, 531 (1990)
H. Horie and A. Arima, “Configuration Mixing and Quadrupole Moments of Odd Nuclei,” Phys. Rev. 99, 778 (1955)

About the Author

John Wood received his Ph.D. from Clark University in 1971 for experimental work on the structure of deformed nuclei. He then took up an interest in the systematic behavior of nuclear structure. This evolved into the experimental study of nuclear structure with radioactive beams and the phenomenology and theory of shape coexistence in nuclei. He is the coauthor of a recent monograph on the fundamentals of nuclear models. He has been at Georgia Institute of Technology since 1972 and is now a professor emeritus in the School of Physics.

Spins, Electromagnetic Moments, and Isomers of ${}^{107 − 129}{Cd}$

D. T. Yordanov, D. L. Balabanski, J. Bieroń, M. L. Bissell, K. Blaum, I. Budinčević, S. Fritzsche, N. Frömmgen, G. Georgiev, Ch. Geppert, M. Hammen, M. Kowalska, K. Kreim, A. Krieger, R. Neugart, W. Nörtershäuser, J. Papuga, and S. Schmidt

Phys. Rev. Lett. 110, 192501 (2013)

Published May 6, 2013

Read PDF