Wave-Shaping Surfaces

Andrea Alù

Viewpoint

Wave-Shaping Surfaces

Department of Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX 78712, USA

May 6, 2013• Physics 6, 53

Ultrathin screens made of metamaterials can bend or reshape a wave transmitted through them without generating any reflection.

Figure caption — **Figure 1:** (a) Conventional optical lenses for focusing or defocusing a beam. These devices operate based on the accumulation of a phase delay and therefore are commonly much larger than the wavelength of operation. (b) Huygens metasurfaces can achieve similar effects by locally controlling electric ( $J_{e}$ ) and magnetic ( $J_{m}$ ) currents induced on the surface. The effect is obtained over a subwavelength thickness, with no reflection and large transmission efficiency.

Controlling light has fascinated mankind since the dawn of civilization, and the centuries of studies leading to the development of modern optics can still be a great source of inspiration. The advent of metamaterials—artificial materials with unconventional properties built by assembling smaller-than-wavelength constituent elements—has opened new venues for the manipulation of light propagation. Now, writing in Physical Review Letters, Carl Pfeiffer and Anthony Grbic from the University of Michigan, Ann Arbor, report the experimental demonstration, inspired by a three-century-old optical principle, of a new “metasurface”: a metamaterial-based thin screen capable of reshaping, in arbitrary ways, a radio-frequency wave transmitted through it, while at the same time minimizing undesired reflections [1].

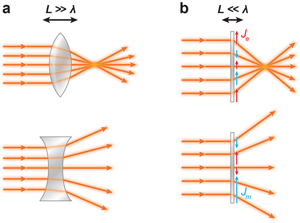
Lenses and prisms were common tools well before the principles of modern optics had been established. Their design and operation is based on the fact that, as light propagates in a material different than air, it accumulates a phase delay along its optical path. By tailoring the shape of their entrance and exit faces, as shown in Fig. 1(a), one can change the total phase accumulation of the transmitted beam, point by point, leading to the ability of focusing, collimating, diffracting, or refracting light. These are inherently volumetric effects, implying that the relevant dimensions of these devices are larger, often much larger, than the wavelength of operation. This may not sound like a big deal for visible wavelengths—shorter than one micrometer—but it actually represents an important limitation for the miniaturization of optical devices like lenses, waveguides, beam formers, and polarizers, and for their integration into nanophotonic and optoelectronic systems. At longer wavelengths, this limitation becomes even more problematic, leading, for example, to the typically bulky designs of radio-astronomy antennas.

To address these limitations, researchers have been investigating new concepts to realize thin structures that rely on surface, rather than volumetric effects. Not by chance, these ideas were first explored and realized at longer wavelengths (radio waves), leading to the realization of frequency-selective surfaces (FSS) [2]. FSS are built of many small patterned elements, which can tailor a wave front to a certain degree by controlling, point by point, how the wave is scattered. So-called reflectarrays [3] and transmitarrays [4] are complex combinations of FSS elements that have become established tools in modern radio-antenna engineering.

Similar concepts have been recently extended to optical wavelengths by using arrays of plasmonic nanoparticles [5,6]. Two recent studies [6] have experimentally shown that suitably designed ultrathin metasurfaces can control the propagation of transmitted light by introducing abrupt phase jumps as the wave hits the surface. Such phase discontinuities are produced by resonant nanostructures (V-shaped plasmonic “nanoantennas”) that are much smaller than the wavelength and can be designed to imprint an arbitrary phase pattern onto the transmitted beam. These solutions, however, have intrinsic limitations, stemming from the symmetries of this design and from the fact that the scheme needs to operate with orthogonally polarized incident and transmitted waves: the reflected beam is necessarily as intense as the transmitted beam, which is often not desirable, and, as we recently showed theoretically [7], the maximum transmission coupling into the desired beam cannot exceed a fundamental limit of $25 %$ in this configuration.

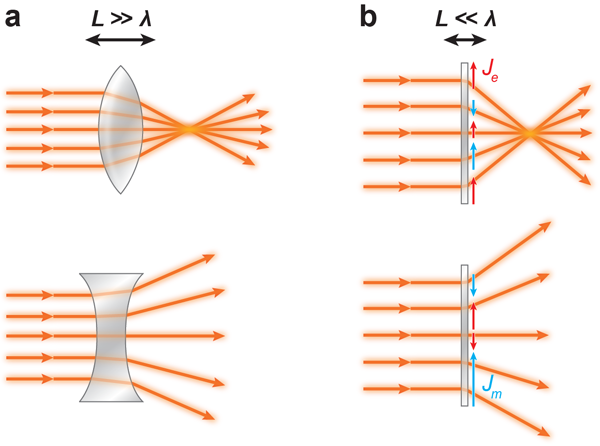
Now, Pfeiffer and Grbic have found an elegant way to overcome these limitations at radio frequencies. Their solution was inspired by the principle introduced by Huygens in 1678 [8] to qualitatively explain how light propagates. According to the Huygens principle, each point on a wave front may be considered as a secondary source of spherical waves, and the sum of all secondary waves determines the wave propagation beyond the wave front. In the $20$ th century, this concept has been more rigorously formulated as the “surface equivalence principle,” widely used in modern antenna engineering [9]: the field distribution over a surface can be modeled with “fictitious” electric and magnetic currents. These equivalent sources allow calculation of the exact field distribution at any point beyond that surface without knowing the true source distribution that originally produced it.

Pfeiffer and Grbic apply this principle to engineer thinner-than-wavelength metasurfaces that can modify the propagation of an incident wave. The authors printed, over a ceramic laminate, suitably shaped metallic inclusions that generate, when excited by the incoming wave, the electric- and magnetic-current profiles needed, according to the surface equivalence principle, to produce a certain field distribution. The concept is illustrated in Fig. 1(b): an inhomogeneous ensemble of subwavelength metallic shapes can locally control the induced electric (red in the figure) and magnetic (blue) currents through its interaction with the incident wave. The result is a new type of FSS, termed by the authors a “Huygens metasurface,” able to imprint, point by point, the desired phase discontinuity on the transmitted beam, with large transmission efficiency and at the same time to avoid unwanted reflections. What enabled this approach has been the idea of controlling both electric- and magnetic-induced currents on the surface, while previous attempts typically considered electric effects only. The symmetries that limited the scheme of Ref. [6] can be avoided by suitably tailoring the transverse magnetic currents, which radiate antisymmetric fields on the two sides of the surface. To be sustained, however, transverse magnetic currents require loops perpendicular to the screen, which implies a finite minimum thickness. In the proposed realization, the metasurface is $6$ mm thick, around $1 / 5$ of the wavelength at the operating frequency of $10$ gigahertz. Even thinner designs may be possible, although this would compromise the device performance.

The authors illustrate how this new concept may enable full control of wave transmission by realizing structures that perform two complex functionalities: bending an impinging wave by up to $80^{\circ}$ and transforming an incident Gaussian beam into a transmitted Bessel beam. The metasurfaces featured large transmission efficiency, close-to-zero reflections, and the ability to operate over a relatively broad spectrum of frequencies. Compared to more conventional transmitarrays, this technology can lead to thinner and simpler designs, and offers superior flexibility in wave manipulation. It may be applied to polarization control, beam shaping and rerouting, focusing, and possibly more advanced forms of optical manipulation with subwavelength spatial resolution.

The question of how to extend these concepts to optical wavelengths remains open, as magnetism becomes naturally weaker as the wavelength shrinks, a consequence of the small value of the fine-structure constant that characterizes the relative strength of electric and magnetic interactions in nature [10], but solutions may be available exploiting the collective resonance of arrays of plasmonic nanoparticles arranged in specific patterns (e.g., Ref. [11]). Recently, my research group has proposed an alternative scheme that may be better suited for optical wavelengths, as it does not rely on magnetic effects: we have theoretically proven that the conditions to realize, as in Pfeiffer and Grbic’s design, full control of the transmitted wave and close-to-zero reflections, may be achieved by using a subwavelength symmetric stack of three closely spaced inhomogeneous metasurfaces composed of two alternating optical materials (silicon and aluminum-zinc oxide) [7].

It is remarkable how Huygens’ ideas have inspired, several centuries later, a promising new technology for designing optical and radio-wave components that may be integrated in compact, planar systems. One day, this may allow bringing the complex optics of a lab onto a small chip or inside the board of our pocket cameras.

References

C. Pfeiffer and A. Grbic, “Metamaterial Huygens’ Surfaces: Tailoring Wave Fronts with Reflectionless Sheets,” Phys. Rev. Lett. 110, 197401 (2013)
B. A. Munk, Frequency Selective Surfaces: Theory and Design (Wiley, New York, 2000)[Amazon][WorldCat]
D. M. Pozar, S. D. Targonski, and H. D. Syrigos, “Design of Millimeter Wave Microstrip Reflectarrays,” IEEE Trans. Antenn. Propag. 45, 287 (1997)
D. McGrath, “Planar Three-Dimensional Constrained Lenses,” IEEE Trans. Antenn. Propag. 34, 46 (1986); D. M. Pozar, “Flat Lens Antenna Concept Using Aperture Coupled Microstrip Patches,” Electronics Lett. 32, 2109 (1996)
B. Memarzadeh and H. Mosallaei, “Array of Planar Plasmonic Scatterers Functioning as Light Concentrator,” Opt. Lett. 36, 2569 (2011)
N. Yu, P. Genevet, M. A. Kats, F. Aieta, J.-P. Tetienne, F. Capasso, and Z. Gaburro, “Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction,” Science 334, 333 (2011); X. Ni, N. K. Emani, A. V. Kildishev, A. Boltasseva, and V. M. Shalaev, “Broadband Light Bending with Plasmonic Nanoantennas,” 335, 427 (2012)
F. Monticone, N. Mohammadi Estakhri, and A. Alù, “Full Control of Nanoscale Optical Transmission with a Composite Metascreen,” Phys. Rev. Lett. 110, 203903 (2013)
C. Huygens, Traitè de la Lumière (Leyden, 1690)
S. Schelkunoff, “Some Equivalence Theorems of Electromagnetics and their Application to Radiation Problems,” Bell Syst. Tech. J. 15, 92 (1936)
R. Merlin, ”Metamaterials and the Landau–Lifshitz Permeability Argument: Large Permittivity Begets High-Frequency Magnetism,” Proc. Natl. Acad. Sci. U.S.A. 106, 1693 (2009)
A. Alù, A. Salandrino, and N. Engheta, “Negative Effective Permeability and Left-Handed Materials at Optical Frequencies,” Opt. Express 14, 1557 (2006); F. Shafiei et al., “A Subwavelength Plasmonic Metamolecule Exhibiting Magnetic-Based Optical Fano Resonance,” Nature Nanotech. 8, 95 (2013)

About the Author

Andrea Alù is an Associate Professor and David & Doris Lybarger Endowed Faculty Fellow at The University of Texas at Austin. He received his Ph.D. in electronic engineering in 2007 from the University of Roma Tre, Italy. After a postdoctoral fellowship at the University of Pennsylvania, in 2009 he joined the faculty at UT Austin. His current research interests span a broad range of areas, including metamaterials and plasmonics, electromagnetic theory and applications, nanooptics and photonics, and acoustics. Over the last few years, he has received several awards for his research work, including the OSA Adolph Lomb Medal (2013), the IUPAP Young Scientist Prize in Optics (2013), the SPIE Early Career Investigator Award (2012), the URSI Issac Koga Gold Medal (2011), the NSF CAREER award (2010), the AFOSR (2010) and DTRA (2011) Young Investigator Award. He is an IEEE and an OSA Fellow, an APS Outstanding Referee, and an OSA Traveling Lecturer. For more information, please see http://users.ece.utexas.edu/~aalu.