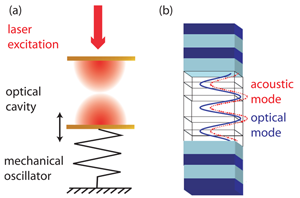
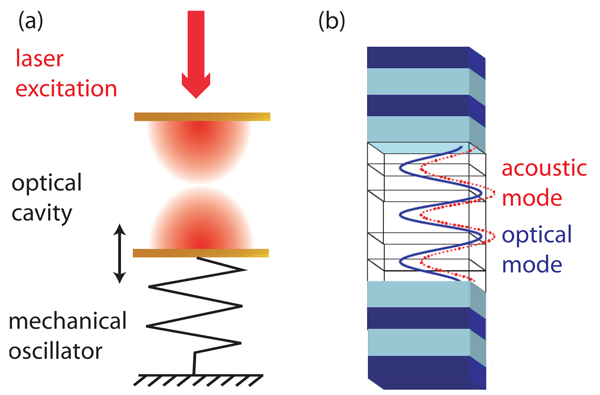
Double Magic Coincidence in an Optomechanical Laser Cavity
Vertical cavity surface emitting lasers (VCSELs) are stacks of tens of different semiconductor layers that constitute the basic components of the lasers: mirrors, optical cavity, and active material. Contrary to edge-emitting lasers, which use the cleaved faces of the semiconductor device as mirrors to confine the photon field laterally, VCSELs provide a laser emission along the stacking axis of the heterostructure. Thanks to this specific geometry that offers unique optical properties, VCSELs could be developed in an impressively wide research field, covering both applied physics and fundamental phenomena. These semiconductor lasers are good candidates for the realization of widely tunable solid state laser sources [1] and have applications in high-speed optical interconnects (in the datacom and telecom range of wavelengths) [2] and gas spectroscopy ( – micron range) [3]. And more than this, thanks to advances in semiconductor growth in the late nineties, VCSELs also emerged in the field of strong light-matter coupling, with the observation of 2D light-matter quasiparticles called exciton-polaritons that can form Bose-Einstein condensates [4] with superfluid properties [5]. More recently, these devices have been used to study the strong coupling between a single quantum dot exciton and a cavity mode in pillar geometries [6]. And despite the impressive number of publications on this kind of optical cavity, the VCSEL spring continues to flow.
Writing in Physical Review Letters, Alejandro Fainstein at the Atomic Center in Bariloche, Argentina, and co-workers demonstrate that VCSELs are also promising systems for investigating the interaction between light and a moving object (optomechanics) [7]. Taking advantage of the simultaneous and equal confinement of photonic and phononic modes within VCSELs of specific composition, which they call “double magic coincidence,” Fainstein et al. demonstrate a large optomechanical coupling in their device, paving the way towards strong acoustic amplification and even sasing (the acoustic analog of lasing) in these systems.
Optomechanics had long remained a theoretical research field before technological advances enabled the fabrication of micro-optomechanical devices, highly sensitive to small vibrations and their coupling to photons. For five years, this research field experienced an impressive blooming triggered by the seminal work of Kippenberg and Vahala [8]. When light couples to mechanical modes in an optical resonator, the cavity-enhanced radiation pressure [see Fig. 1(a)] can result in two opposite phenomena: optical cooling and vibrational amplification [9]. If the first could be used to cool down small systems without resorting to conventional cryogenics, the latter (also known as parametric instability) can lead to stimulated phonon emission in the gigahertz [10] or terahertz range [11]. Conversely, optomechanics has become a good means to explore optical processes too, for example, in the work of Watanabe et al., who probed the excitonic transitions in a semiconductor heterostructure though the mechanical oscillations of the system [12]. In these efforts, however, most of the optomechanical systems under scrutiny consisted of suspended designs (toroidal cavities, cantilevers, membranes, and so on) as they favor mechanical vibrations. The subsequent fragility of these devices limited their practical use. This difficulty could be surpassed in the case of VCSELs, which are instead monolithic and robust structures.
The VCSEL used by Fainstein et al. is made of a cavity grown in between distributed Bragg reflectors (DBR) [see Fig. 1(b)]. These reflectors are periodic structures composed of layers of semiconductors with different refractive index, namely, and , in which multiple reflections constructively interfere to provide a very high reflection coefficient over a wide frequency range (the so-called DBR stop band). For this specific choice of materials (which is, by the way, extremely common in the microcavity community) a surprising coincidence occurs: acoustic and photonic modes share almost the same propagation properties despite their different natures, resulting in an equal confinement for phonons and photons of the same wavelength. For a -nanometer-thick cavity, this corresponds to photons with wavelength of nanometers (nm) and phonons of frequency gigahertz (GHz). This “double magic coincidence” magnifies the acousto-optical coupling in the VCSEL. The optical wavelength of , close to the band gap, is chosen so that two mechanisms contribute to the optomechanical coupling. On the one hand, the radiation pressure inside the cavity pushes apart the Bragg reflectors, just like in the scheme of Fig. 1(a). On the other hand, the strains induced by this deformation also produce a local modification of the refractive index that can be particularly high for excitation wavelengths close to the absorption edge of the material.
To probe the strength of this optomechanical coupling, Fainstein et al. perform an optical pump-probe experiment. When the microcavity is resonantly excited with the pump optical pulse, phonons are generated in the cavity by both the electrostrictive and deformation potential mechanisms. In the time domain, the reflectivity of the microcavity starts beating at acoustic frequencies. Equivalently, in the frequency domain, phonon sidebands appear in the reflectivity spectrum. The Fourier transform of the probe beam differential reflectivity as a function of the pump-probe delay thus gives access to the optomechanical coupling between the optical cavity mode and the confined acoustic modes. The reported results indicate that the coupling factor in VCSELs would be two orders of magnitude above the best near-infrared optomechanical systems, with a major contribution from the photoelastic effect. The authors also mention that, by improving the geometry of their system using pillar geometries and higher reflectivity DBRs, the parametric instability could occur in the milliwatt range. However, the coupling factors measured in the present work and the ones of other optomechanical systems are obtained with very different experimental schemes: a pulsed excitation in the work of Fainstein et al. and continuous wave excitation in the other cases. Additional investigation would be useful to check that this difference does not harm the comparison.
Another question arising from this new experiment deals with the coupling to acoustic modes at and . Indeed these modes do not lie within the main acoustic stop band of the DBRs. But harmonic stop bands are also expected at ( ) multiples of the fundamental frequency if one neglects the dependence of the acoustic impedance with frequency. That’s why in the present case, and acoustic modes seem well confined and participate in the optomechanical coupling. However, the observed decay of the coupling strength with increasing frequency is not reproduced by the authors’ calculation. As the harmonic stop bands get narrower with increasing frequency, a small mismatch between the cavity length and the DBR periodicity could then make the higher-energy cavity modes progressively exit the stop bands, providing an explanation for the weakening of the coupling at high acoustic frequencies.
In a nutshell, the VCSEL may indeed emerge as the mandatory geometry for stimulated sound emission. It features extremely high optomechanical coupling factors and has an interestingly robust design. But the practical use of stimulated sound emission still has to come up. Will the saser buzz spread beyond the scientific community far to the application world?
References
- V. Jayaraman, G. D. Cole, M. Robertson, A. Uddin, and A. Cable, “High-Sweep-Rate 1310 nm MEMS-VCSEL with 150 nm Continuous Tuning Range ,” Electron. Lett. 48, 867 (2012)
- W. Hofmann, M. Müller, P. Wolf, A. Mutig, T. Gründl, G. Böhm, D. Bimberg, and M.-C. Amann, “40 Gbit/s Modulation of 1550 nm VCSEL ,” Electron. Lett. 47, 270 (2011)
- G. Boehm, A. Bachmann, J. Rosskopf, M. Ortsiefer, J. Chen, A. Hangauer, R. Meyer, R. Strzoda, and M.-C. Amann, “Comparison of InP- and GaSb-based VCSELs Emitting at 2.3 m suitable for carbon monoxide detection,” J. Cryst. Growth 323, 442 (2011)
- J. Kasprzak et al., “Bose–Einstein Condensation of Exciton Polaritons,” Nature 443, 409 (2006)
- A. Amo et al., “Superfluidity of Polaritons in Semiconductor Microcavities,” Nature Phys. 5, 805 (2009)
- E. Peter, P. Senellart, D. Martrou, A. Lemaître, J. Hours, J. M. Gérard, and J. Bloch, “Exciton-Photon Strong-Coupling Regime for a Single Quantum Dot Embedded in a Microcavity,” Phys. Rev. Lett. 95, 067401 (2005)
- A. Fainstein, N. D. Lanzillotti-Kimura, B. Jusserand, and B. Perrin, “Strong Optical-Mechanical Coupling in a Vertical GaAs/AlAs Microcavity for Subterahertz Phonons and Near-Infrared Light,” Phys. Rev. Lett. 110, 037403 (2013)
- T. J. Kippenberg, H. Rokhsari, T. Carmon, A. Scherer, and K. J. Vahala, “Analysis of Radiation-Pressure Induced Mechanical Oscillation of an Optical Microcavity,” Phys. Rev. Lett. 95, 033901 (2005)
- T. J. Kippenberg and K. J. Vahala, “Cavity Optomechanics: Back-Action at the Mesoscale,” Science 321, 1172 (2008)
- I. S. Grudinin, H. Lee, O. Painter, and K. J. Vahala, “Phonon Laser Action in a Tunable Two-Level System,” Phys. Rev. Lett. 104, 083901 (2010)
- R. P. Beardsley, A. V. Akimov, M. Henini, and A. J. Kent, “Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice,” Phys. Rev. Lett. 104, 085501 (2010)
- T. Watanabe H. Okamoto, K. Onomitsu, H. Gotoh, T. Sogawa, and H. Yamaguchi, “Optomechanical Photoabsorption Spectroscopy of Exciton States in GaAs,” Appl. Phys. Lett. 101, 082107 (2012)