Closer to a Quantum Internet

Philip Hemmer

Viewpoint

Closer to a Quantum Internet

Electrical & Computer Engineering Department, Texas A&M University, College Station, TX 77843, USA

May 28, 2013• Physics 6, 62

A demonstration of photon-pair generation from visible to telecom wavelengths may speed the development of quantum networks.

Figure caption — **Figure 1:** Illustration of the entanglement of two distant quantum memories, operating at different wavelengths, using telecom photons transmitted over an internet fiber. Operation of the photon-pair source at the wavelengths shown on the left was demonstrated in the paper by Fekete *et al.* [1]. The source on the right can be constructed by the same approach and is easier to realize because the generated wavelengths are closer. In this example, entanglement is created by measurement of identical $1436 nm$ photons, each produced by a different photon-pair source and interfered on a $50 %$ beam splitter.

It has been nearly two decades since quantum computation first captured the imagination of the general public as a potential way to break the toughest cryptographic codes. Now, quantum information systems are becoming a reality, not for code breaking but as code generators whose security is governed by the laws of physics rather than computational complexity. This gives quantum communication systems an advantage over classical systems whose codes could, in principle, always be broken by some clever algorithm or a quantum computer. Yet there is still a key stumbling block to the construction of the quantum internet: transmitting quantum information over long distances. In a paper in Physical Review Letters, Julia Fekete at the Institute of Photonic Sciences, Spain, and colleagues report the first demonstration of a spectrally narrow-band source of photon pairs where one photon can address solid-state quantum memories at visible wavelengths, and the other is at a wavelength where telecommunications systems operate [1]. This is a critical element of a telecom-compatible quantum repeater and therefore brings us one step closer to the realization of a quantum internet.

As in a classical communication scheme, quantum information can be transmitted using infrared photons in optical fibers. However, photons decay exponentially as they propagate, limiting the maximum communication distances to about 100 kilometers. In classical networks, this problem is solved by using repeaters consisting of photon amplifiers. However, these are not practical in a quantum internet because amplification degrades quantum entanglement. Hence quantum repeaters are needed [2].

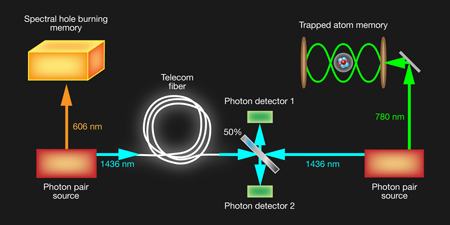
Such repeaters, like their classical counterparts, divide long communication lines into shorter ones by inserting repeater “nodes.” Entanglement is first established between adjacent nodes using, for example, entangled photon-pair sources. This entanglement “resource” is then purified or “amplified” by performing quantum operations in the nodes. The entanglement can then be extended to nonadjacent nodes, and so on, by entanglement swapping or teleportation, until long distances can be covered. Finally, the quantum information is teleported. In this way the quantum signal is transmitted without exponential degradation and without being amplified. The basic teleportation protocols were demonstrated previously using photons [3,4]. However, achieving the entanglement amplification, and hence long distance quantum communication, requires that the entanglement resources be stored in quantum memories in each node long enough to test that the fidelity is high enough. Quantum networks of the future will also need to be flexible enough to connect quantum processors of widely different technologies (Fig. 1).

In recent years, researchers have made much progress in the construction of long-term quantum memories for photons. For example, systems based on ensembles of quantum units, like atomic vapors and spectral hole burning (SHB) crystals, have shown encouraging results. SHB crystals store information in the form of reversible “notches” that are created in their optical absorption spectra at specific frequencies, and they have shown storage times in excess of seconds [5] and efficiencies up to $69 %$ [6]. The SHB approach has the advantage of being able to store many photon qubits in each crystal [7]. Recently, photons in SHB memories were entangled with telecom photons, proving that quantum internet nodes are possible with this technology [8,9]. However, there is a problem: quantum memories, like SHB, can only work with photons at a very precise frequency or wavelength. On the other hand, telecom-compatible photo-pair generators create photons whose frequencies span a much broader spectrum. In other words, a large fraction of the spectrum provided by photon-pair generators cannot be processed by existing quantum memories. This limitation has now been overcome by Fekete et al.

The broad spectrum of photon-pair generators derives from the spontaneous parametric down-conversion (SPDC) process used to produce pairs of entangled photons whose wavelengths differ wildly (i.e., visible vs telecom band): In SPDC, a pump photon is split into two longer wavelength photons with frequency uncertainties that are typically $> 100$ gigahertz. But typical quantum optical memories require the frequency to be specified with precision on the order of tens of megahertz. Of course, optical filtering is possible, but this greatly reduces the number of usable photon pairs that can be generated per second. To overcome this problem, the SPDC can be forced to emit photons with less frequency uncertainty by placing it in a resonant optical cavity so that photon pairs are only generated at frequencies corresponding to narrow cavity resonances [10,11]. Yet this does not completely eliminate the need for spectral filtering, as the SPDC gain linewidth is so large that multiple optical cavity modes are excited.

To limit the number of active modes, two approaches have been explored. “Clustering” uses the fact that different wavelengths have different refractive indices so that most of the cavity modes are not triply resonant (i.e., for input and the two output photon wavelengths). Thus the SPDC emits in only a few adjacent or clustered modes [12]. A second approach is to use a very short cavity so that the modes are spaced by a large wavelength gap. Unfortunately, both of these approaches have only worked so far by using output photon wavelengths that were nearly the same. Making one of these methods work for widely different wavelengths is a significant technical challenge that was solved by Fekete et al.

In their demonstration, Fekete et al. used the clustering approach wherein one photon of each output pair was resonant with a $Pr$ doped $Y_{2} {SiO}_{5}$ (Pr:YSO) crystal operating at $606$ nanometers (nm), which can function as a high-fidelity quantum memory, and the other photon was well into the telecom band at $1436 nm$ , more than twice the wavelength. The $1436 nm$ photon can then be transmitted down an optical fiber to the next node where the quantum entanglement can be stored in another memory using, for example, measurement-based entanglement [13], as illustrated in Fig. 1.

Since the $Pr : YSO$ wavelength is farther from the telecom band than most quantum memory technologies, it is clear that the approach can be easily extended to other promising memories such as $Tm$ doped ${LiNbO}_{3}$ , $Nd$ doped $Y_{2} {SiO}_{5}$ , ${Ca}^{+}$ ions, and atomic rubidium and cesium.

Consequently, this work represents an important milestone toward the construction of a long-distance quantum internet. The next step would be to combine this photon-pair generator with two remote optical memories, of the same or different technology, and demonstrate entanglement of these memories via telecom fibers. Then the protocol could be extended beyond the nearest-neighbor nodes, eventually including entanglement amplification to enable construction of a long-distance wide-scale quantum internet.

References

J. Fekete, D. Rieländer, M. Cristiani, and H. de Riedmatten, “Ultranarrow-Band Photon-Pair Source Compatible with Solid State Quantum Memories and Telecommunication Networks,” Phys. Rev. Lett. 110, 220502 (2013)
H.-J. Briegel, W. Dür, J. I. Cirac, and P. Zoller, “Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication,” Phys. Rev. Lett. 81, 5932 (1998)
D. Boschi, S. Branca, F. De Martini, L. Hardy, and S. Popescu, “Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels,” Phys. Rev. Lett. 80, 1121 (1998)
D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, and A. Zeilinger, “Experimental Quantum Teleportation,” Nature 390, 575 (1997)
J. J. Longdell, E. Fraval, M. J. Sellars, and N. B. Manson, “Stopped Light with Storage Times Greater than One Second Using Electromagnetically Induced Transparency in a Solid,” Phys. Rev. Lett. 95, 063601 (2005)
M. P. Hedges, J. J. Longdell, Y. Li, and M. J. Sellars, “Efficient Quantum Memory for Light,” Nature 465, 1052 (2010)
M. S. Shahriar, P. R. Hemmer, S. Lloyd, P. S. Bhatia, and A. E. Craig, “Solid-State Quantum Computing Using Spectral Holes,” Phys. Rev. A 66, 032301 (2002)
E. Saglamyurek et al., “Broadband Waveguide Quantum Memory for Entangled Photons,” Nature 469, 512 (2011)
C. Clausen, I. Usmani, F. Bussières, N. Sangouard, M. Afzelius, H. de Riedmatten, and N. Gisin, “Quantum Storage Of Photonic Entanglement in a Crystal,” Nature 469, 508 (2011)
J. S. Neergaard-Nielsen, B. Melholt Nielsen, H. Takahashi, A. I. Vistnes, and E. S. Polzik, “High Purity Bright Single Photon Source,” Opt. Express 15, 7940 (2007)
M. Scholz, L. Koch, R. Ullmann, and O. Benson, “Single-Mode Operation of a High-Brightness Narrow-Band Single-Photon Source,” Appl. Phys. Lett. 94, 201105 (2009)
C.-S. Chuu, G. Y. Yin, and S. E. Harris, “A Miniature Ultrabright Source of Temporally Long, Narrowband Biphotons,” Appl. Phys. Lett. 101, 051108 (2012)
L.-M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, “Long-Distance Quantum Communication with Atomic Ensembles and Linear Optics,” Nature 414, 413 (2001)

About the Author

Philip Hemmer received his B.S. in physics from the University of Dayton, and his Ph.D. in physics from MIT. He worked many years as a physicist for the Air Force Research Laboratory at Hanscom Air Force Base, MA. Since 2002, he has been with the Electrical & Computer Engineering Department at Texas A&M University. His current research interests include quantum optics especially with nitrogen-vacancy diamond, subwavelength imaging, quantum computing in solids, plasmon-based nano-optics, slow and stopped light, and ultrasound imaging.