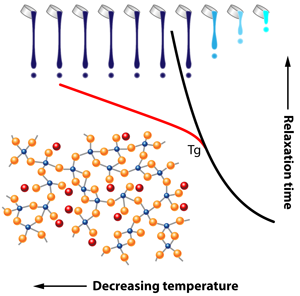
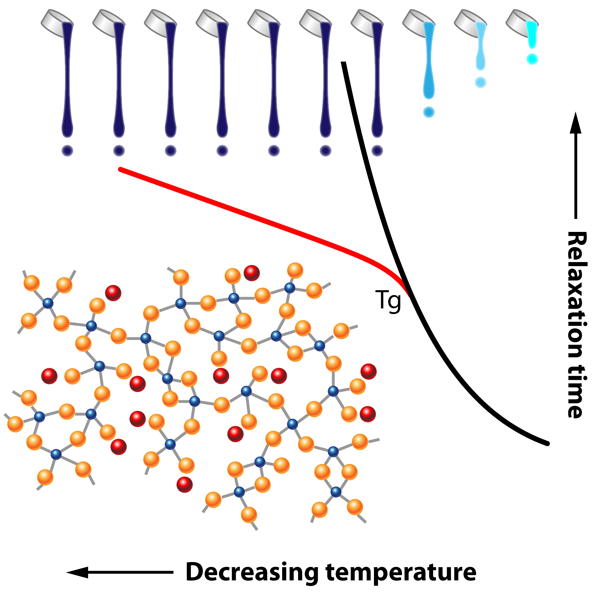
The Deep Effect of Topology on Glass Relaxation

Matthieu Micoulaut

Viewpoint

The Deep Effect of Topology on Glass Relaxation

Laboratoire de Physique Théorique de la Matière Condensée, Boite 121, Université Pierre et Marie Curie, CNRS UMR 7600, 4 Place Jussieu, 75252 Paris Cedex 05, France

June 24, 2013• Physics 6, 72

Measurement of ambient strain in a large glass plate shows structural relaxation far away from the glass transition region and reveals details of the underlying atomic network topology.

Figure caption — **Figure 1:** As the temperature is decreased, the viscosity of a supercooled liquid becomes exponentially large and so does the relaxation time towards equilibrium (black curve). Welch *et al.* [1] have shown that in a commercial glass plate, the relaxation time behavior in the nonequilibrium glassy state changes at the glass transition temperature $T_{g}$ and is about $19, 000$ years at room temperature (red curve). The relaxation is not a product of viscous flow but rather originates in the nature and the number of relaxation channels. These effects are imposed by the underlying network structure, which is made of an aluminosilicate tetrahedral network disrupted by alkali cations.

The problems posed by glass are not only practical but also conceptual: despite the progress afforded by advances in glass science, we still lack a complete understanding of how a liquid becomes a glass. Indeed, in contrast to most phase transitions, many measureable physical and chemical glass properties change smoothly across the liquid-to-glass transition at the glass transition temperature $T_{g}$ . And in the liquid, the origin of the huge increase of viscosity ( $10^{12}$ pascal-seconds at $T_{g}$ ) remains poorly understood. A similar increase is observed for the relaxation time $τ$ of the system towards thermal equilibrium following an imposed stress (Fig. 1). This relaxation time is still measurable at $T_{g}$ because it is on the order of the timescale of an experiment, but it grows by several orders of magnitude as temperature continues to decrease below $T_{g}$ . As a result, measuring the relaxation of a glass far below its transition temperature remains a true challenge; thus most studies have focused on the supercooled liquid where the relaxation time of the system is less than, or of the order of, the experimental time scale.

In Physical Review Letters [1], Roger Welch and co-workers from Corning Inc., New York, report one of the first detectable signatures of glass relaxation at low (room) temperature. They achieve this by following, for more than a year, the strain in a huge commercial glass plate (Gorilla $^{®}$ Glass, which is used, for example, in smartphone screens) of $1050 \times 1050 \times 0.7 mm$ , which exceeds by far the usual sample sizes investigated for this purpose. When the supercooled liquid is quenched to a glass, strains in the material are “frozen in.” The second and even more surprising feature is that the glass relaxes measurably at much lower temperatures, i.e., $T / T_{g} = 0.3$ (or about $600$ °C below the glass transition temperature), which defies the conventional wisdom that the relaxation time at such low temperatures is far too long to allow for any observable evolution of physical quantities. Indeed, the approximate temperature at which ageing (relaxation) experiments are usually performed [2] is about $T / T_{g} \sim 0.8$ .

Given the timescales involved for relaxation, glasses are systems that are out of thermodynamic equilibrium, and their disordered atomic structure sufficiently impedes crystallization, allowing solidification on large scales as well as the exhibition of residual frozen stresses. This is because atoms are randomly placed in the network, and this situation is energetically unfavorable, at least with respect to a regular crystalline lattice. These stresses can be partially released by moderate temperature annealing, a technique, known by the ancient Phoenicians, that prevents stress-induced cracking. The authors actually succeed in measuring the strain with time, in other words, the relaxation of the glass, and conclude that it follows a so-called Kohlrausch exponent law of the form exp $(- t / τ)^{β}$ , with $β = 0.43$ .

Glass researchers have believed for a long time that $β$ is only a fitting parameter, without any physical meaning. However, it is not a coincidence that the measured value of $β$ for this huge glass plate coincides with a “magic” number proposed by Phillips [3]. During the minimization of internal stresses, density fluctuations are also minimized, and with them, relaxation, driven by short-range forces. Such forces are particularly relevant in network glasses such as the Corning’s Gorilla $^{®}$ Glass used in this study, which is made of a basic aluminosilicate tetrahedral network that is disrupted by alkali cations. In the presence of nanoscale density fluctuations (which are present in pure silica), relaxation follows a simple exponential [4]. The addition of alkali atoms leads to long-range Coulombic forces that can compete with the residual short-range interactions such as bond bending or bond stretching, leading to two possible ways the material can relax. In such a case, Phillips demonstrated [3] that $β$ is simply related to the dimensionality $D$ of the relaxing network via $β = D / (D + 2) = 3 / 5$ , for the case $D = 3$ . However, $D$ can have an effective dimensionality of $3 / 2$ if only one of the two possible relaxation channels is operative, leading ultimately to $β = 3 / 7$ . Thus topology of the glass network obviously governs a large part of the relaxation.

The results from Welch and co-workers [1] and the statement above change the way researchers usually view the glass transition, i.e., that it is a liquid state problem that should be solved with tools from statistical physics of liquids while mostly overlooking important effects due to glass structure or properties. However, a recent report has shown [5] that vibrational properties of the glass well below $T_{g}$ are correlated with the way viscosity or relaxation time changes with temperature in the corresponding supercooled liquid. This is fully in line with the way Welch et al. understand the nature of glassy relaxation from the underlying network properties. Therefore it now provides a strong indication that the low-temperature structure governs large parts of the relaxation at higher temperatures, including in the supercooled liquid.

Furthermore, extended compositional studies on structural glasses [6] have shown that there are deep connections between the underlying network topology of glasses and their associated properties, and the viscous slow down occurring close to the glass transition, thus providing an alternative and unifying viewpoint to the glass transition problem, now seen from the sub- $T_{g}$ side. These aspects are actually also used by some of the authors of Ref. [1] to model more accurate functional forms for liquid and glassy relaxation [7].

Moreover, anomalies in relaxation and the Kohlrausch exponent $β$ observed by our group [8] seem to be intimately related to elastic (flexible to rigid) transitions driven by topological changes in corresponding glasses. Indeed, researchers measure a global minimum in the enthalpy of relaxation at $T_{g}$ in selected composition or pressure ranges (stress-free reversibility windows) in many oxides and chalcogenides glasses [9,10]. The opening of these windows is the signature of network adaptability under increasing stress induced by an increase in bond connectivity that modifies the topology in depth. This obviously has some implications for the glassy relaxation [10], now confirmed by Welch et al.’s strain measurement.

Consequently, the work of Welch et al. [1] represents an important contribution that has both fundamental and applied implications. In the search for a unifying picture of the glass transition problem, features and theoretical modeling of both the liquid and the glass appear to be necessary, while emphasizing the central role of low-temperature network topology in liquid dynamics. Given the connection with elastic phase transitions induced by composition, the next step could be to investigate the effect of the composition of such glasses on the search for optimized functionalities such as those discovered in reversibility windows [9,10]. In fact, from a more practical viewpoint, minimizing internal stresses has an immediate consequence: paradoxically, it makes it possible to manufacture stronger glasses that are less easily damaged by external stresses.

References

R. C. Welch, J. R. Smith, M. Potuzak, X. Guo, B. F. Bowden, T. J. Kiczenski, D. C. Allan, E. A. King, A. J. Ellison, and J. C. Mauro, “Dynamics of Glass Relaxation at Room Temperature,” Phys. Rev. Lett. 110, 265901 (2013)
V. S. Zotev, G. F. Rodriguez, G. G. Kenning, R. Orbach, E. Vincent, and J. Hammann, “Role of Initial Conditions in Spin-Glass Aging Experiments,” Phys. Rev. B 67, 184422 (2003)
J. C. Phillips, “Stretched Exponential Relaxation in Molecular and Electronic Glasses,” Rep. Prog. Phys. 59, 1133 (1996)
M. Vannoni, A. Sordini, and G. Molesini, “Relaxation Time and Viscosity of Fused Silica Glass at Room Temperature,” Eur. Phys. J. E 34, 92 (2011)
T. Scopigno, G. Ruocco, F. Sette, and G. Monaco, “Is the Fragility of a Liquid Embedded in the Properties of Its Glass?” Science 302, 849 (2003)
P. Chen, P. Boolchand, and D. G. Georgeiv, “Long Term Aging of Selenide Glasses: Evidence of sub- $T_{g}$ Endotherms and pre- $T_{g}$ Exotherms,” J. Phys. Cond. Matt. 22, 065104 (2010)
J. C. Mauro, Y. Z. Yue, A. J. Ellison, P. K. Gupta, and D. C. Allan, “Viscosity of Glass-Forming Liquids,” Proc. Natl. Acad. Sci.U.S.A. 106, 19780 (2009)
D. Novita, P. Boolchand, M. Malki, and M. Micoulaut, “Fast-Ion Conduction and Flexibility of Glassy Networks,” Phys. Rev. Lett. 98, 195501 (2007); M. Micoulaut, M. Malki, D. I. Novita, and P. Boolchand, “Fast-Ion Conduction and Flexibility and Rigidity of Solid Electrolyte Glasses,” Phys. Rev. B 80, 184205 (2009)
D. Selvanathan, W. J. Bresser, and P. Boolchand, “Stiffness Transitions in Si $_{x}$ Se $_{1 - x}$ Glasses from Raman Scattering and Temperature-Modulated Differential Scanning Calorimetry,” Phys. Rev. B 61, 15061 (2000); F. Wang, S. Mamedov, P.Boolchand, B. Goodman, and M. Chandrasekhar, “Pressure Raman Effects and Internal Stress in Network Glasses,” Phys. Rev. B 71, 174201 (2005)
B. J. Badhu, H. S. Jayanna, and S. Asokan, Evidence of an Intermediate Phase in Ternary Ge $_{7}$ Se $_{93 - x}$ Sb $_{x}$ glasses,” Eur. Phys. J. 71, 21 (2009); M. Bauchy, and M. Micoulaut, “Transport Anomalies and Adaptative Pressure-Dependent Topological Constraints in Tetrahedral Liquids: Evidence for a Reversibility Window Analogue,” Phys. Rev. Lett. 110, 095501 (2013)

About the Author

Matthieu Micoulaut is Professor of Physics at Université Pierre et Marie Curie (UPMC) in Paris, France http://www.lptl.jussieu.fr/user/mmi. He received his Ph.D. from the same university in 1993. His research centers on the theory of disordered solids, glasses and glass transition, granular media, and out-of-equilibrium processes. In recent years, he has been actively involved in the characterization of new glassy phases with unusual physical properties. He was selected as a Fulbright Fellow for 2013.

Dynamics of Glass Relaxation at Room Temperature

Roger C. Welch, John R. Smith, Marcel Potuzak, Xiaoju Guo, Bradley F. Bowden, T. J. Kiczenski, Douglas C. Allan, Ellyn A. King, Adam J. Ellison, and John C. Mauro

Phys. Rev. Lett. 110, 265901 (2013)

Published June 24, 2013

Read PDF