Squeezing Out More Information About Entanglement

Otfried Gühne; Tobias Moroder

Viewpoint

Squeezing Out More Information About Entanglement

Otfried Gühne

Naturwissenschaftlich-Technische Fakultät, Universität Siegen, Walter-Flex-Straße 3, 57072 Siegen, Germany

Tobias Moroder

Naturwissenschaftlich-Technische Fakultät, Universität Siegen, Walter-Flex-Straße 3, 57072 Siegen, Germany

July 15, 2013• Physics 6, 79

An experimental demonstration of a novel quantum analysis tool will allow diagnosis of entanglement in a much broader set of states.

Figure caption — **Figure 1:** The geometry of entanglement. In the high-dimensional space of all matrices, the set of all quantum states is convex (light blue), and the separable (nonentangled) states form a convex subset (darker blue). An entanglement witness $W$ is a linear function that is positive on all separable states. In the figure, the line denotes the states in which $W$ is zero, the state $ρ_{1}$ is detected as entangled, while the state $ρ_{2}$ is not detected by $W$ . A possible nonlinear improvement $N$ ( $W$ ) of $W$ may detect $ρ_{1}$ and $ρ_{2}$ at the same time, which is impossible with a single linear witness. Agnew *et al.* [1] have experimentally implemented a nonlinear witness that can achieve this in measurements of orbital angular momentum states of photons created in a nonlinear crystal.

To be useful, quantum computers will ultimately need to entangle a large number of qubits. At the same time, researchers studying fundamental quantum physics seek to entangle larger and larger objects. For instance, entanglement of up to fourteen ions or eight photons has been generated and verified. However, rigorously analyzing the quantum properties of such entangled states in these expanded systems is cumbersome with tools available to date, mainly because of difficulties like time-consuming data acquisition or computationally expensive data processing. To overcome these limitations, we need innovative techniques for quantum state analysis. In a paper in Physical Review Letters, Megan Agnew and co-workers at the University of Ottawa, Canada, report one possible approach in their experimental demonstration of an unusually powerful variation on a class of methods called “entanglement witnesses” [1]. Their results open the way to test entanglement in a range of quantum systems previously unreachable.

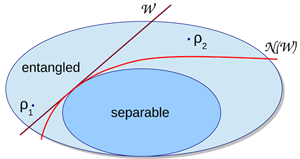
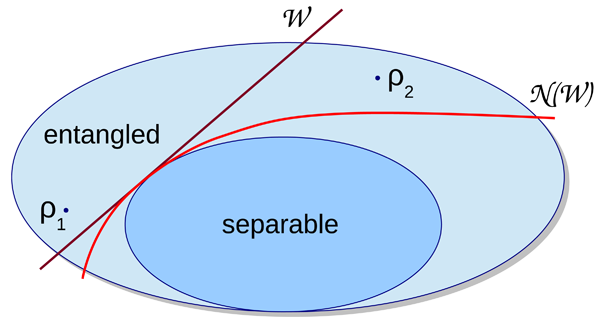
One of the most important signatures of quantum control is the creation of entanglement. Among the important theoretical tools for detecting and quantifying entanglement are so-called “entanglement witnesses” [2], which are special kinds of nonlocal observables of the composite quantum system. The key characteristic of an entanglement witness is that it has a non-negative expectation value for all separable (or nonentangled) states. In other words, if one observes a negative value, one is assured that the underlying state is entangled (see the schematic set diagram in Fig. 1).

Because of their nonlocal structure, entanglement witnesses cannot directly be ascertained by local measurements, but the expectation value is still easy to obtain: One simply measures several types of correlations between the quantum systems and then linearly combines the resulting mean values to compute the value of the nonlocal observable. Such correlations can take the form of experimental polarization measurements onto spatially separated photons, where the correlations might be such that two photons always have the opposite polarization. Geometrically, the set of all separable states is convex, meaning that for any two points in it, the connection line is also in the set. This implies that one can find such an entanglement witness $W$ for any entangled state, as there is always a plane separating an entangled state from the separable states.

However, as shown in the diagram in Fig. 1, for two very different states in the set of entangled states, say $ρ_{1}$ and $ρ_{2}$ , a single linear witness cannot detect both; this would only be possible if one could imagine a curved division. Such a curved separator captures the idea of a nonlinear entanglement witness $N (W)$ , where some correlations are combined in a nonlinear way. Indeed, theoretically it has been shown that any witness can be improved by nonlinear correction terms [3] as well as how one can curve it in a preferred direction [4].

In this new work, Agnew et al. have experimentally implemented such a nonlinear entanglement witness [1]. Remarkably, the nonlinear correction terms for the witness could be evaluated mainly with the same correlation measurements as the original witness. The constructed nonlinear witness is then capable of detecting a much larger fraction of all entangled states than the single original linear witness.

In their experiment, Agnew et al. use the orbital angular momentum of light to generate entanglement. Photons with orbital angular momentum have a helical phase distribution (like a corkscrew) that can be described by a quantum number $ℓ$ . When a photon impinges on a specially chosen crystal, it generates two photons. If the incoming pump photon has zero angular momentum, the two resulting output photons are found to be in a superposition of states, where one photon is in state $| ℓ 〉$ and the other one in the state $| - ℓ 〉$ [5]. The resulting entangled state has then been further transformed using devices called Dove prisms, and in the actual experimental setup this allowed Agnew et al. to controllably generate all four Bell states (the maximally entangled states for two spin- $1 / 2$ particles). The properties of orbital angular momentum entangled states have attracted many researchers in the last years, since it allows the creation of entanglement between many degrees of freedom [6], in contrast to polarized photons or trapped ions. This has benefits, for instance, in quantum communication tasks.

Agnew et al. start with a linear witness based on the fidelity of the quantum state, that is, the extent to which the experimentally prepared state equals the intended ideal Bell state. It can be viewed as a lower bound on the fidelity: If the fidelity is above a certain threshold, then the state is detected as entangled. Since the fidelity of an entangled state is not directly measurable, one circumvents this problem by measuring certain correlations that are typical for the Bell state.

In the present setup, six correlations are needed to determine the linear witness. A correlation measurement in the experiment consists of filtering each photon depending on the orbital angular momentum and testing whether both photons are detected behind the filter. For constructing the nonlinear witnesses, the team from Ottawa used a theoretical proposal put forward by Arrazola and co-workers [7]. The main idea of this proposal is that the formation of the linear witness does not use all of the available information. Thus one can use the correlations that were already measured for determining the fidelity to form the nonlinear terms that improve the witness. In this way, the nonlinear evaluation scheme extracts additional information and leads to an improved entanglement detection scheme. For the case of two qubits, the resulting nonlinear witness enables the detection of two Bell states at the same time, a feat no linear witness can perform.

The experiment carried out by Agnew et al. constitutes only a first proof-of-principle demonstration of a nonlinear entanglement witness. For the present case of two qubits, many other analysis tools, such as the determination of the complete density matrix by quantum state tomography or the evaluation of several linear entanglement witnesses from the same data, are available and all of them can be used to verify the entanglement in the current experiment. However, as soon as more parties or higher-dimensional systems come into play, full quantum state tomography becomes intractable and the systematic construction of linear entanglement witnesses is hard—at that point, a set of very powerful nonlinear entanglement witnesses become especially handy.

From a broader perspective, the work of Agnew et al. is one of several recent approaches to improve and simplify the tools for analyzing quantum experiments, especially if only very limited information about a larger quantum system is available. One topic under investigation is the analysis of quantum correlations when only some observables are accessible. For instance, only time-of-flight measurements are possible for ultracold rubidium atoms in optical lattices, but entanglement can still be characterized [8]. A second approach is the development of adaptive entanglement detection schemes, in which the observables are chosen on the basis of previous measurement results [9]. A third topic addresses the careful statistical analysis of entanglement witnesses or state reconstruction schemes (for an example concerning nonlinear entanglement witnesses see Ref. [10]). Finally, many groups currently work on the problem to characterize other useful properties of quantum states besides entanglement in a fast way, such as the ability to generate a secret key in quantum cryptography or the usability for quantum enhanced measurements. These analysis tools, together with the results of Agnew et al., will help our experimental colleagues to evaluate their future experiments with large quantum systems.

References

M. Agnew, J. Z. Salvail, J. Leach, and R. W. Boyd, “Generation of Orbital Angular Momentum Bell States and Their Verification via Accessible Nonlinear Witnesses,” Phys. Rev. Lett. 111, 030402 (2013)
O. Gühne and G. Tóth, “Entanglement Detection,” Phys. Rep. 474, 1 (2009)
O. Gühne and N. Lütkenhaus, “Nonlinear Entanglement Witnesses,” Phys. Rev. Lett. 96, 170502 (2006)
T. Moroder, O. Gühne, and N. Lütkenhaus, “Iterations of Nonlinear Entanglement Witnesses,” Phys. Rev. A 78, 032326 (2008)
A. Mair, A. Vaziri, G. Weihs, and A. Zeilinger, “Entanglement of the Orbital Angular Momentum States of Photons,” Nature 412, 313 (2001)
A. C. Dada, J. Leach, G. S. Buller, M. J. Padgett, and E. Andersson, “Experimental High-Dimensional Two-Photon Entanglement and Violations of Generalized Bell Inequalities,” Nature Phys. 7, 677 (2011)
J. M. Arrazola, O. Gittsovich, and N. Lütkenhaus, “Accessible Nonlinear Entanglement Witnesses,” Phys. Rev. A 85, 062327 (2012)
M. Cramer, A. Bernard, N. Fabbri, L. Fallani, C. Fort, S. Rosi, F. Caruso, M. Inguscio, and M. B. Plenio, “Entanglement of Bosons in Optical Lattices,” arXiv:1302.4897
W. Laskowski, D. Richart, C. Schwemmer, T. Paterek, and H. Weinfurter, “Experimental Schmidt Decomposition and State Independent Entanglement Detection,” Phys. Rev. Lett. 108, 240501 (2012)
J. M. Arrazola, O. Gittsovich, J. M. Donohue, J. Lavoie, K. J. Resch, and N. Lütkenhaus, “Reliable Entanglement Verification,” Phys. Rev. A 87, 062331 (2013)

About the Authors

Otfried Gühne obtained his Ph.D. from the University of Hannover, Germany, in 2004. After that, he moved to Innsbruck in Austria, first as a postdoc and, since 2008, as a leader of a junior research group. Since 2010 he has been a professor at the University of Siegen in Germany. His research interests are the theory of multiparticle entanglement and the foundations of quantum mechanics.

Tobias Moroder received his Ph.D. from the University of Erlangen-Nuremberg, Germany, in 2009, but most of his Ph.D. work was carried out in Waterloo, Canada. After postdoctoral research in Innsbruck he is now working in the group of Otfried Gühne in Siegen. His research interests include quantum key distribution, entanglement theory, and optimization theory in quantum information.