A Long-Term Memory for Light
The ability to store light while keeping its quantum coherence properties (e.g., entanglement) plays an important role in quantum information science. It makes it possible to build quantum memories for light, which could become crucial elements in many quantum information processing schemes based on the use of photons, from quantum communication networks to quantum computing protocols. A critical parameter for applications is the duration over which light can be stored. For example, the distribution of quantum bits over complex quantum information networks, and their storage for further manipulation, might require quantum memories with storage time from a few seconds to a few minutes. Writing in Physical Review Letters, Georg Heinze at the University of Darmstadt, Germany, and colleagues report an important step towards this goal by demonstrating a solid-state coherent optical memory capable of storing a classical light pulse, and even a full image, for a duration of more than one minute—the longest light-storage time reported in any system to date [1].
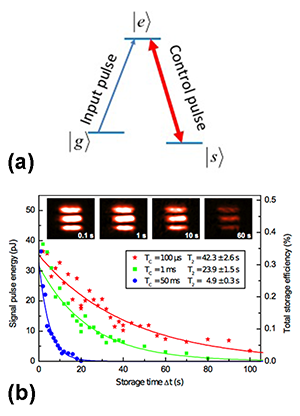
To stop and retrieve light pulses without destroying their quantum coherence, light coherence needs to be converted into atomic coherences. This can be achieved with electromagnetically induced transparency (EIT), a quantum interference effect that makes an opaque medium transparent over a narrow spectral range. In EIT, a control laser beam excites atomic systems with two ground spin states connected to an excited state by optically allowed transitions [see Fig. 1(a)]. Through destructive interference, the transition probability between one of the ground states and the excited state (hence the absorption at the corresponding frequency) vanishes. The change of absorption results in a very steep change of refractive index that reduces the group velocity of an incoming light pulse. Light can be slowed down to the point that it comes to a halt: by switching off the control beam when the light is within the sample, the photons can be converted into collective atomic spin excitations (so called spin waves) [2]. The spin waves can be stored in the atoms for as long as the coherence between the two spin levels survives, before being converted back into light by turning on the control pulse again. The scheme thus allows the coherent storage and retrieval of light.
How long can the storage time be? Since the light is stored in atomic coherences, the limit is given by , quantifying the lifetime of the coherence between the two relevant atomic spin states (how long the two spin states can remain in a coherent superposition). The fundamental limit for is given by , the spin population relaxation time (the average time over which an individual spin loses its excitation): . However, can be much shorter: any interaction between the atoms and their environment will induce decoherence and reduce . The experimental challenge is therefore to isolate the atoms as much as possible from their environment to increase the coherence time of the spin transition.
EIT in atomic gases was first used to stop classical light in 2001 [3], and later to store single photons for durations of the order of microseconds ( ) in atomic gases [4], confirming that the principle can work in the quantum regime. The main limitation to the storage time in atomic gases is the random motion of the atoms, which causes dephasing of the spin waves. In 2013, the limitation was mitigated by placing the atoms in an optical lattice, limiting the atomic motion and allowing a storage time of seconds (s) for classical pulses [5].
While solid-state devices would be preferable for applications, stopping light in solids is more challenging: stronger interactions between atoms and their environment severely limit the attainable coherence times. But the effect has been demonstrated in a special class of solids: crystals doped with rare-earth (RE) ions [6] cooled at cryogenic temperatures. Since the atoms are naturally trapped in the crystal, the motion of RE atoms is limited and the transitions of interest take place between electronic levels (e.g., the electrons of praseodymium) shielded from the crystal environment by outer full electronic shells ( and ). This makes the coherence properties of these crystals exceptional.
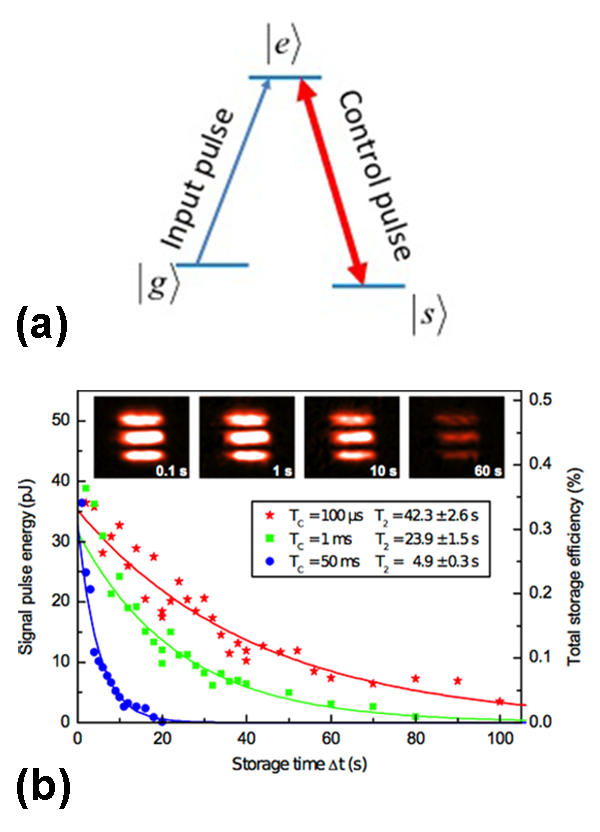
Heinze and colleagues used a silicate crystal of yttrium doped with ), in which the population lifetime is of the order of , suggesting a potentially long storage time. The main obstacle here is posed by the lifetime of the coherence between the two states ( ), which is much shorter ( ). But while poses a fundamental limit, there are ways to control . By using external magnetic fields with controlled amplitude and direction, researchers have indeed been able to reduce the impact of various mechanisms of decoherence [7], pushing close to . Further improvements were achieved by a technique based on the use of radio frequency pulses [8] that can decouple the spins from their environment, leading to the demonstration of a spin coherence of up to [9] as well as to light storage for more than [10].
By combining the above-mentioned techniques with powerful algorithms for the optimization of their experimental parameters, Heinze et al. go one step further: they push the storage time up to a minute, very close to the fundamental limit posed by the population relaxation lifetime. One of the challenges is that the magnetic fields used lead to a very complex hyperfine energy-level structure of the atoms (up to transitions may couple to the laser). This jungle of levels requires an optimal optical pumping sequence (in terms of laser intensities and frequencies) to prepare the EIT-based memory. To help them in this daunting task, Heinze and colleagues used a so-called evolutionary algorithm (an optimization algorithm inspired by biological evolution, which uses mechanisms such as mutation, recombination, and selection) to find the best parameters for their pumping lasers. Similarly, they used another algorithm (automatic gradient-search) to determine the optimal magnetic field for maximizing the value.
An interesting aspect of the work is that the memory is spatially multimode: the authors store a classical image (consisting of three -micrometer-long horizontal stripes) for more than one minute [see Fig. 1(b)]. The result outperforms earlier demonstrations in atomic gases by about six orders of magnitude and offers exciting possibilities of long-storage-time quantum memories that are spatially multiplexed, i.e., can store different quantum bits as different pixels.
The experiment represents a beautiful example of the ability to control decoherence processes and light-matter interaction in a solid-state environment. However, the demonstration was done with classical bright pulses, and several challenges need to be overcome to extend this scheme to the quantum regime. First, the technical noise introduced by the methods for increasing must not prevent operation at the single photon level. Second, the narrow spectral window of the EIT effect would require using the quantum memory in combination with quantum light sources with comparable bandwidth (less than megahertz). This remains a challenging task, although progress has been reported in that direction [11]. Finally, the efficiency of the storage ( in the present scheme) will have to be significantly increased for applications.
Will it be possible to achieve significantly longer storage times? This seems difficult for since the present results are very close to a fundamental limit. But there might be better materials. In , for example, the spin population lifetime can approach several days at low temperature, while the coherence time at zero field is milliseconds, times longer than in . While in this material the control of with optimal magnetic field remains largely unexplored, there is clear hope that this could be a solid-state platform able to achieve coherent light storage for tens of minutes.
References
- G. Heinze, C. Hubrich, and T. Halfmann, “Stopped Light and Image Storage by Electromagnetically Induced Transparency up to the Regime of One Minute,” Phys. Rev. Lett. 111, 033601 (2013)
- M. Fleischhauer and M. D. Lukin, “Dark-State Polaritons in Electromagnetically Induced Transparency,” Phys. Rev. Lett. 84, 5094 (2000)
- C. Liu, Z. Dutton, C. H. Behroozi, and L. Vestergaard Hau, “Observation of Coherent Optical Information Storage in an Atomic Medium Using Halted Light Pulses,” Nature 409, 490 (2001); D. F. Phillips, A. Fleischhauer, A. Mair, R. L. Walsworth, and M. D. Lukin, “Storage of Light in Atomic Vapor,” Phys. Rev. Lett. 86, 783 (2001)
- T. Chanelière, D. N. Matsukevich, S. D. Jenkins, S.-Y. Lan, T. A. B. Kennedy, and A. Kuzmich, “Storage and Retrieval of Single Photons Transmitted Between Remote Quantum Memories,” Nature 438, 833 (2005); M. D. Eisaman, A. André, F. Massou, M. Fleischhauer, A. S. Zibrov, M. D. Lukin, and M. D. Eisaman, “Electromagnetically Induced Transparency with Tunable Single Photon Pulses,” 438, 837 (2005)
- Y. O. Dudin, L. Li, and A. Kuzmich, “Light Storage on the Time Scale of a Minute,” Phys. Rev. A 87, 031801 (2013)
- A. V. Turukhin, V. S. Sudarshanam, M. S. Shahriar, J. A. Musser, B. S. Ham, and P. R. Hemmer, “Observation of Ultraslow and Stored Light Pulses in a Solid,” Phys. Rev. Lett. 88, 023602 (2001)
- E. Fraval, M. J. Sellars, and J. J. Longdell, “Method of Extending Hyperfine Coherence Times in Pr:YSiO,” Phys. Rev. Lett. 92, 077601 (2004)
- L. Viola, E. Knill, and S. Lloyd, “Dynamical Decoupling of Open Quantum Systems,” Phys. Rev. Lett. 82, 24172421 (1999)
- E. Fraval, M. J. Sellars, and J. J. Longdell, “Dynamic Decoherence Control of a Solid-State Nuclear-Quadrupole Bit,” Phys. Rev. Lett. 95, 030506 (2005)
- J. J. Longdell, E. Fraval, M. J. Sellars, and N. B. Manson, “Stopped Light with Storage Times Greater than One Second Using Electromagnetically Induced Transparency in a Solid,” Phys. Rev. Lett. 95, 063601 (2005)
- J. Fekete, D. Rieländer, M. Cristiani, and H. de Riedmatten, “Ultranarrow-Band Photon-Pair Source Compatible with Solid State Quantum Memories and Telecommunication Networks,” Phys. Rev. Lett. 110, 220502 (2013)