Turning the Wheels of a Quantum Motor
If you searched the web for “quantum motors,” you would be pleased to find that, for less than $400, you can purchase one from the eponymous company. Unfortunately, the quantum you get for your money is in the brand name, not the products (which, in this case, are used for remote controlled aircraft.) Quantum motors, it seems, are not yet a reality.
But perhaps the quantum motor is an idea whose time has come. As reported in Physical Review Letters, Raúl Bustos-Marún of the Free University of Berlin, Germany, and colleagues have developed a theoretical scheme to describe such motors, which allowed them to calculate their efficiency for the first time [1]. This work could be useful for motivating and designing future experiments, and exploring fundamental questions about how quantum machines work. Quantum motors could be used to perform tasks on length scales far smaller than those researchers can reach today. For example, one might spin a ring-shaped molecule like benzene in a controllable way.
The garden-variety electric motor in a car and the quantum motor of Ref. [1] are both driven by electric currents. But how they operate is fundamentally different. In standard electric motors, a torque on a current-carrying loop is produced by its interaction with a magnetic field. In the quantum motor, no magnets are present. Instead, what drives the motor is interference between the quantum mechanical waves that describe electrons in the current. To understand how this works, we need to explain the mechanism underlying a related device: the quantum electron pump.
Many motors are simply pumps run backwards. For example, the Archimedean screw, which dates to the 3rd century BC, uses (manual) work to elevate water. But run backwards, it functions as a water turbine, a machine from the 3rd century AD that uses the potential energy of water at a high elevation to do work. Similarly, a quantum pump functions as a tiny transistor that uses voltage gates to transport charge, while a quantum motor uses the transport of charge to manipulate the gates.
Excitement over quantum pumps began with a series of theoretical papers in 1998 [2,3] followed in 1999 by an experimental demonstration from Switkes et al. of a new type of working pump for electrons. The pumping action in a quantum pump exploits the fact that electrons are described by quantum-mechanical waves. Now, unlike familiar pumps that transport particles (a vacuum cleaner) or heat (a refrigerator), a pump that sucks up waves is an odd beast: if it were operating on waves of light, we could call it a “black torch.” If you think a little about how such a wave pump might work, you will recognize the usefulness of interference. Interference is a consequence of the fact that, unlike particles, waves do not choose one orbit but rather explore all available paths in space. Interference is then a sensitive probe of changes in the geometry of this. An example would be a periodic manipulation of the slits in the Young double-slit experiment, which would lead to a moving interference pattern. If the interference pattern can be forced to move in one direction, the device behaves as a wave pump.
This was the idea behind Switkes et al.’s experiment. Two metallic electron reservoirs were connected by a region whose landscape was shaped by voltage barriers (hurdles for electrons) and voltage sinks (electron traps). As the researchers cycled the landscape through different shapes, the interference patterns formed by the electron waves changed, leading to the transport of charge from one reservoir to another.
How can one tell a wave pump from a particle pump? The electrons at the Fermi surface of the reservoirs are moving at high speeds. If electrons were just particles, they would be moving too fast to notice that the pump is not idle. However, being waves, the head of the wave experiences slightly different conditions than its tail. The electron interferes with itself and can tell that the pump is not idle.
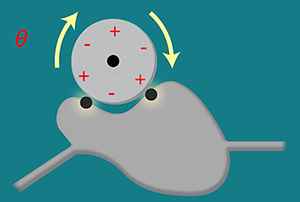
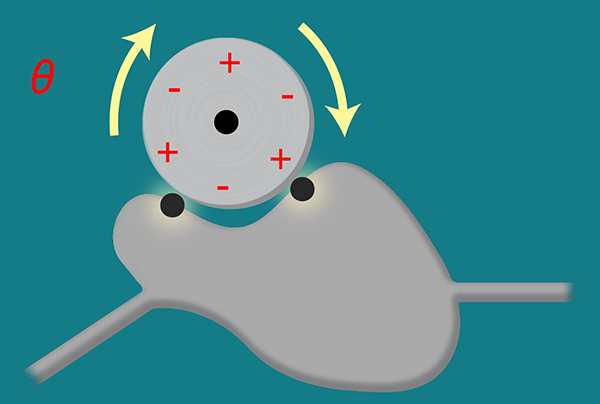
In their work, Bustos-Marún et al. consider the inversion of an electron pump: instead of an electron current responding to external controls, the current drives the motion of the old controls. In particular, the authors consider the possibility that these “controls” could be alternating charges pinned to a freely rotating “wheel” (see Fig. 1). They developed a mathematical model for electronic quantum motors by building on the original theory of quantum pumps [2]. (Both models rely on a formalism that describes the way electron waves scatter in a slowly changing potential [4].) Their model allows them to analyze how the pinned charges in the pinwheel in Fig. 1 would respond to the cycle of destructive and constructive interference patterns of the electron current.
The model allows them to compute the work that a current, driven by a difference in chemical potentials, performs on the pinwheel. By comparing the charge transported when the motor is frozen to the charge transported when it is running, they arrive at a definition of efficiency of motors and find an interesting relationship: If their theoretical motor operates at 100% efficiency, it will, when run backwards, function as a quantized pump (a device, called a Thouless pump, that transports an integer number of electrons in a cycle).
How far are we from being to able to make a quantum motor? Experiments on motors are likely to be harder than the Switkes et al. experiment [5] on pumps. This is because nanotechnology is not at the point that a freely rotating nanopinwheel can be constructed, let alone mounted on a minute transistor. Moreover, Switkes et al.’s experiment did not perfectly match all the predictions of the theory of quantum pumps, indicating the challenges to replicating a theoretical scheme in the lab.
References
- R. Bustos-Marún, G. Refael, and F. von Oppen, “Adiabatic Quantum Motors,” Phys. Rev. Lett. 111, 060802 (2013)
- P. W. Brouwer, “Scattering Approach to Parametric Pumping,” Phys. Rev. B 58, 10135 (1998)
- I. L. Aleiner and A. V. Andreev, “Adiabatic Charge Pumping in Almost Open Dots,” Phys. Rev. Lett. 81, 1286 (1998)
- M. Büttiker, H. Thomas, and A. Prêtre “Current Partition in Multiprobe Conductors in the Presence of Slowly Oscillating External Potentials,” Z. Phys. B 94, 133 (1994)
- M. Switkes, C. M. Marcus, K. Campman, and A. C. Gossard, “An Adiabatic Quantum Electron Pump,” Science 283, 1905 (1999)