Quantum Chaos on Display
In most systems encountered in our everyday life, small changes in the initial conditions can lead to widely diverging outcomes. Think, for example, of the drawing of lottery numbers. Even if great care was taken in the initial positioning of the balls, and the lottery machine was set in an almost identical rotation, we could hardly expect the same outcome at every draw. Although governed by deterministic laws, such a system is unpredictable. In classical physics, the phenomenon of extreme sensitivity to initial conditions is what defines chaos. Since classical mechanics is only an approximation of the more fundamental theory of quantum mechanics, one may expect to see analogous behavior in the quantum world. However, the laws of quantum mechanics do not permit a similar definition, since they do not lead to exponential sensitivity to the initial conditions. So how does classical chaos emerge from a quantum system? Are there any signatures of chaos in a quantum system whose classical counterpart is chaotic? In Physical Review A, Jonas Larson at Stockholm University, Sweden, and colleagues [1] propose that such questions—at the heart of the research field known as quantum chaos [2,3]—could be addressed experimentally in an ideal model system: an ultracold atomic gas in which an artificial spin-orbit (SO) coupling is induced by laser fields.
Over recent decades, researchers have learned some important things about the relationship between quantum mechanics and classical chaos. One of the most solid conclusions concerns the statistical properties of the energy levels of large quantum systems [3], such as heavy atomic nuclei. If a classically nonchaotic system is quantized, the resulting discrete energy values (eigenvalues) tend to cluster, while eigenvalues in quantum systems whose classical counterparts are chaotic typically repel each other and tend to be distributed more uniformly within the available energy range. These signatures of chaos have been experimentally observed in the energy levels obtained from atomic and molecular spectra.
Such energy-level statistics are primarily related to the static properties of a quantum system. Chaotic behavior, however, emerges in the first place in the dynamics of a system, i.e., in how it changes with time. From an experimental perspective, the observation of quantum dynamics is challenging, requiring exquisite control of system parameters and good isolation from the environment, in order to protect quantum mechanical wave functions from decoherence. As is often the case, the physics of cold atomic gases comes to the rescue, offering a highly controllable platform for the realization of theoretically predicted effects.
Dynamical models of quantum chaos have been previously demonstrated in beautiful experiments involving cold atoms in optical traps [4]. Chaudhury et al. [5] have recently realized a so-called “kicked quantum top.” The kicked top—a prototype model for chaotic behavior—can be thought of as a spinning top, in which chaos is induced by a sequence of periodic driving kicks. Chaudhury’s quantum top is made of an ensemble of cold cesium-133 atoms, whose angular momentum is kicked by laser and magnetic fields. The authors observed a good correspondence between the quantum and the classical system: In chaotic regimes, the quantum dynamics exhibited a more pronounced sensitivity with respect to perturbations in the Hamiltonian, reminiscent of the exponential sensitivity to initial conditions found in classical chaos.
The progress in the manipulation of cold atoms in turn provides inspiration for new research avenues for the field of quantum chaos. The latest rabbit pulled out of the cold-atom hat has been the demonstration of spin-orbit-coupled Bose-Einstein condensates [6]. In cold atoms, an effective spin-orbit coupling can be artificially engineered by using lasers that induce a position dependence for two internal states (the “spin”). Now, the work of Larson et al. shows that spin-orbit coupling could be used as a control knob that switches a cold-atom ensemble between regular and chaotic behavior.
Larson et al. analyze the dynamical behavior of a dilute spin-orbit coupled gas of atoms. To investigate the quantum-classical correspondence and to base their analysis on the firmer ground of classical chaos, the authors first address the classical dynamics of the system. Since the spin degree of freedom is inherently quantum mechanical, the system does not have a trivially identifiable classical counterpart. However, Larson et al. show that a classical counterpart in the usual sense can be found by describing the system within a Born-Oppenheimer approximation (in which the spin and orbital motions are separated). Furthermore, they show that the behavior of this classical counterpart can be switched from nonchaotic, if the spin orbit coupling is isotropic, to chaotic, if the coupling is directionally dependent (anisotropic). The authors go on to analyze the quantum dynamics, initiated by what is called a “quantum quench”: After preparing the system in its ground state in the optical trap, they imagine slightly moving the trap, thus creating a nonequilibrium condition that evolves with time. They then simulate the long-term dynamics of the perturbed system for the two spin-orbit coupling symmetries that correspond to a chaotic and nonchaotic classical counterpart, searching for the fingerprints of chaos.
The key chaos-related question addressed by the author is whether the quantum system thermalizes, e.g., relaxes to a state in which expectation values no longer change and which is distributed more or less evenly over the allowed energy manifold. In isolated classical systems, thermalization is associated to chaos: In the presence of chaos, the particles’ motions can explore the entirety of the phase space, which allows reaching a fully thermal redistribution. The details of quantum thermalization are still poorly understood, but by the correspondence principle, one would expect that the quantum counterparts of classically chaotic systems also show thermalization [7]. This is indeed what the authors find in their calculations. Thermalization of the quantum system is only observed when the classical counterpart is chaotic. The authors further calculate the expected timescales of such thermalization processes, and their findings support previous speculations that these are directly related to the rate by which initially close trajectories separate in the corresponding classical system. Thermalization thus seems to be a key signature of quantum chaos.
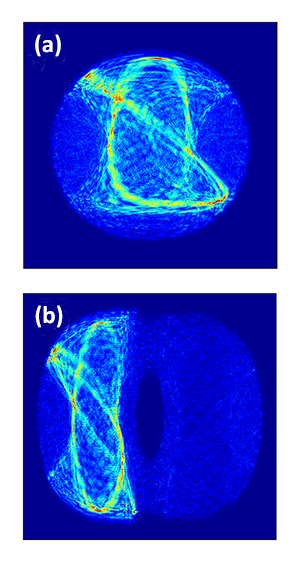
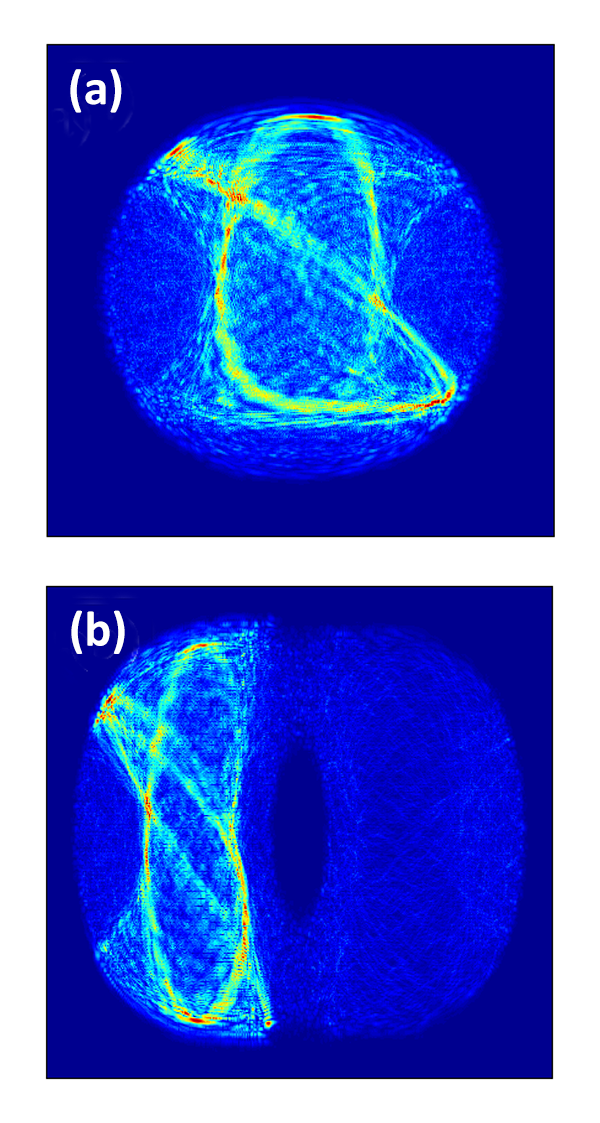
A compelling aspect of the work of Larson et al. is the predicted observation of so-called “quantum scars” [8,9]. In a classically chaotic system, dynamic trajectories—due to their instability to perturbations—eventually explore the whole space. One would thus expect that quantum trajectories, as smeared-out versions of their classical counterparts, would spread out in time all over the available space. However, in a classical system, there are specific initial conditions for which the system moves back and forth along a closed, periodic trajectory, hidden in the chaotic sea. Such closed trajectories leave high-density “scars” in some steady-state eigenfunctions of the corresponding quantum system (see Fig. 1). Larson et al. have argued that similar scars can be observed in the thermalized states of spin-orbit-coupled cold atoms after a long time evolution. In their theorized cold-atom experiment, the scarred distribution could be made directly visible, providing a spectacular demonstration of the quantum signatures of chaos.
The system proposed by Larson et al. would allow a comprehensive investigation of the physics of quantum chaos and the recent demonstrations of spin-orbit-coupled gases of bosons suggest that a realization of their ideas may soon be within reach. Their approach might then help address a key unresolved question: What drives—at the quantum mechanical level—the process of thermalization? If, e.g., an ensemble of molecules thermalizes, it must be because quantum mechanics tells them to. But how? Quantum chaos may provide one of the key missing pieces for solving this important puzzle.
References
- J. Larson, B. M. Anderson, and A. Altland, “Chaos-driven dynamics in spin-orbit-coupled atomic gases,” Phys. Rev. A 87, 013624 (2013)
- M. V. Berry, “Quantum Chaology,” Proc. R. Soc. London A 413, 183 (1987)
- F. Haake, Quantum Signatures of Chaos (Springer Verlag, Berlin, 2010)[Amazon][WorldCat]
- M. Raizen and D. A. Steck, “Cold Atom Experiments in Quantum Chaos,” Scholarpedia 6, 10468 (2011)
- S. Chaudhury, A. Smith, B. E. Anderson, S. Ghose, and P. S. Jessen, “Quantum Signatures of Chaos in a Kicked Top,” Nature 461, 768 (2009)
- Y. J. Lin, K. Jimenez-Garcia, and I. B. Spielman, “Spin-Orbit Coupled Bose-Einstein Condensates,” Nature 471, 83 (2011)
- M. Rigol, V. Dunjiko, and M. Olshanii, “Thermalization and its Mechanism for Generic Isolated Quantum Systems,” Nature 452, 854 (2008)
- E. J. Heller, “Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits,” Phys. Rev. Lett. 53, 1515 (1984)
- E. J. Heller and S. Tomsovic, “Postmodern Quantum Mechanics,” Phys. Today 46, No. 7, 38 (1993)