Subtle Atomic Shifts
Multiferroics are materials that combine electric and magnetic functionalities. Though still at the research stage, these materials have potential applications in spintronics and data storage, including high-speed memory with magnetically and electrically addressable states, magnetically tunable switches and sensors. All of these applications rely on a fundamental interaction between the electric and magnetic states of the material, called magnetoelectricity. Yet despite years of research, it has been unclear how this interaction occurs on the atomic level. In Physical Review B, Sanghyun Lee, from Seoul National University in Korea, and colleagues now report new insight into the dominant microscopic mechanism that drives magnetoelectricity in one of the most studied multiferroics, [1].
Discovered in the 1970s, multiferroics combine two (or more) types of ferroic ordering, most commonly, ferroelectricity and either ferromagnetism or antiferromagnetism [2]. In a ferroelectric crystal, each unit cell carries an electric polarization that arises from a relative shift of positive and negative ions. An applied electric field can reverse this polarization simply by moving the atoms. Similarly, the unit cell of a ferromagnetic crystal carries a magnetic moment from the net alignment of magnetic ions, and this moment can be rotated by an applied magnetic field. (An antiferromagnet is also magnetically ordered, but neighboring magnetic moments cancel out.) What makes multiferroics interesting and useful for applications is that the ferroelectric and magnetic orderings are coupled: a magnetic field can control the ferroelectric polarization, and an electric field can control the magnetic structure. This property is particularly interesting for making devices with switchable magnetic states: most multiferroics are insulators and in such materials it is more energy efficient to manipulate voltages to make electric fields than it is to generate currents to make magnetic fields. Numerous groups around the world are actively seeking new ways to cast multiferroics in thin-film form for the purpose of making new types of electronic devices [3].
One complication with developing an atomic-level picture of magnetoelectricity in multiferroics is that these systems belong to the class of “frustrated magnets,” meaning one magnetic ion cannot simultaneously satisfy all of its interactions with its magnetic neighbors. In such frustrated systems, the spins tend to arrange in complex patterns. For example, the spins may not all point along a single axis, or they can form spirals that have a different periodicity than the lattice itself. In such systems, a coupling between the magnetic order and ferroelectric order can occur because the magnetic interactions are more energetically favorable if the atoms make small changes in their positions. Two types of magnetic interaction drive these shifts: the symmetric superexchange Heisenberg interaction between two spins and ( ) and the antisymmetric Dzyaloshinskii–Moriya exchange interaction ( ). Here, is the Dzyaloshinskii vector and the interaction comes from a relativistic correction to the usual superexchange that has a strength proportional to the spin–orbit coupling constant.
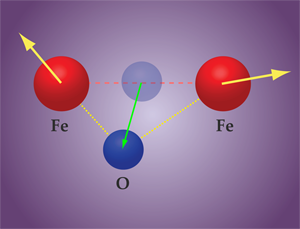
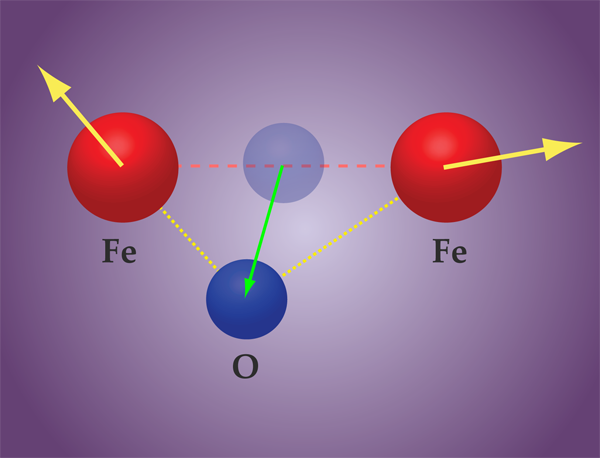
Researchers have debated which magnetic interaction plays a stronger role in creating magnetoelectricity in a multiferroic. In the inverse Dzyaloshinskii-Moriya (DM) scenario, the nonalignment of neighboring spins acts as a force that displaces oppositely charged ions and, in turn, generates an electric polarization. Figure 1 shows the effect in a magnetic material containing iron ( ) and oxygen ( ): the force pushes the bonding oxygen atom away from the - bond. The DM effect always induces an electric polarization that lies within the rotation plane of the spins and is perpendicular to the magnetic bond [4]. In the symmetric Heisenberg exchange striction model, a shift in bond distances or angles results in a more energetically favorable spin configuration from the point of view of symmetric exchange.
To see which of these effects is more prominent, Lee et al. performed a neutron scattering experiment to carefully study the relationship between the magnetic structure and the atomic positions in a single crystal of [1]. Among known multiferroics, is probably the most promising: its electric and antiferromagnetic order both occur at temperatures below rather high transition points ( kelvin and kelvin, respectively), making it suitable for room-temperature applications. The material also has a high electric polarization (over microcoulombs per centimeter squared). And for this kind of study, neutron scattering is an ideal probe. The experiment, which the authors performed at the Laue-Langevin Institute in Grenoble, France, uses the wave properties of neutrons to look at diffraction (Bragg) peaks associated with the crystalline and magnetic order in the material. Changes in the atomic positions lead to changes in the intensities of the diffraction peaks, which the authors can use to figure out how the positively charged Fe and bismuth ( ) atoms move with respect to the negatively charged oxygen ions above and below the antiferromagnetic ordering transition.
By measuring the atomic positions, Lee et al. were able to calculate the electric polarization of individual atoms. In , it turns out that the polarization produced by the inverse DM coupling below the magnetic transition enhances the existing polarization (which is already in place at this temperature). In contrast, the symmetric exchange striction induced polarization can be positive or negative: it can enhance or reduce the existing polarization. Lee et al. showed that a reduction in the polarization at was more prominent than the enhancement, meaning that the magnetostrictive magnetoelectric coupling induces a stronger electric polarization than the inverse DM effect does.
This is not the first experiment to cast doubt on the DM scenario. One clue came from studying excitations found in multiferroics called “electromagnons” [5]. These excitations are similar to the spin waves that occur in magnets, but should be considered as hybrid spin-lattice excitations that carry an electric dipole as result of the magnetoelectric coupling. Optical studies of these excitations in multiferroic materials, including [6], have shown that the selection rules for making the excitations are consistent with the magnetostriction model, but not the DM scenario.
We now have different experimental techniques pointing to exchange striction as the origin of magnetoelectric coupling in multiferroics. Confirmation that this mechanism is the leading one will nonetheless require further detailed and systematic studies of other multiferroics with different magnetic and crystal structures. In this pursuit, Lee et al.’s work has shown that a modern high-luminosity neutron source is an essential tool for solving fundamental problems in materials science. A related topic worth investigating is “magnonics,” which is the study of how electric and magnetic fields can be used to handle electromagnons. In any case, the example of multiferroics shows that magnetic frustration is a powerful source of unconventional magnetic order, which can induce exciting new physics and potentially lead to new applications.
Note (22 August 2013): The figure was revised.
References
- S. Lee et al., “Negative magnetostrictive magnetoelectric coupling of BiFeO,” Phys. Rev. B 88, 060103 (2013)
- S. W. Cheong and M. Mostovoy, “Multiferroics: A Magnetic Twist for Ferroelectricity,” Nature Mater. 6, 13 (2007)
- V. Garcia, S. Fusil, K. Bouzehouane, S. Enouz-Vedrenne, N. D. Mathur, A. Barthélémy, and M. Bibes, “Giant Tunnel Electroresistance for Non-Destructive Readout of Ferroelectric States,” Nature Mater. 460, 81 (2009)
- H. Katsura, A. V. Balatsky, and N. Nagaosa, “Dynamical Magnetoelectric Coupling in Helical Magnets,” Phys. Rev. Lett. 98, 027203 (2007)
- A. Pimenov, A. A. Mukhin, V. Yu. Ivanov, V. D. Travkin, A. M. Balbashov, and A. Loidl, “Possible Evidence for Electromagnons in Multiferroic Manganites,” Nature Phys. 2 97 (2006)
- M. Cazayous, Y. Gallais, A. Sacuto, R. de Sousa, D. Lebeugle, and D. Colson, “Possible Observation of Cycloidal Electromagnons in BiFeO3,” Phys Rev. Lett. 101, 037601 (2008)