Is the Lopsided Universe an Open Universe?

Marc Kamionkowski

Viewpoint

Is the Lopsided Universe an Open Universe?

Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD 21218, USA

September 9, 2013• Physics 6, 98

The recently confirmed sky-wide asymmetry in the cosmic microwave background might be explained by assuming the Universe is slightly curved just beyond the cosmic horizon.

Figure caption — **Figure 1:** (Top) In this full sky map, the CMB temperature fluctuations on large scales are more extreme on the right side of the sky. (Bottom) According to the open inflation model, our Universe was born via bubble nucleation inside a larger metauniverse, depicted here with two space dimensions. From the metauniverse perspective, the bubble forms at time $T_{0}$ and expands outward, as shown with red rings at times $T_{1}$ , $T_{2}$ , and $T_{3}$ . In the three-dimensional spacetime, this expansion forms a “bubble wall” that acts as the starting point ( $t_{0}$ ) of our Universe. Subsequent times ( $t_{1}$ , $t_{2}$ , $t_{3}$ ) are defined on hypersurfaces above the bubble wall. The yellow lines show the trajectories of constant positions in space inside this open Universe.

The density of matter and energy appears to vary more strongly on one side of the sky versus the other. That surprising assessment is based on corroborating evidence from two recent in-depth studies of the cosmic microwave background (CMB)—the thermal radiation left over from the big bang. To explain this hemispheric asymmetry, previous models [1] assumed the distribution of matter/energy fluctuations behaves differently beyond a particular distance scale, which is just a bit larger than the size of the observable Universe. However, the origin of this fundamental distance scale was left unexplained. Now, Andrew Liddle and Marina Cortês of the University of Edinburgh, UK, postulate [2] that this distance scale may represent the radius of curvature in a negatively curved (or “open”) Universe. In Physical Review Letters, the researchers show how a curvature-induced asymmetry can arise naturally if the Universe is open and was born via a process called bubble nucleation.

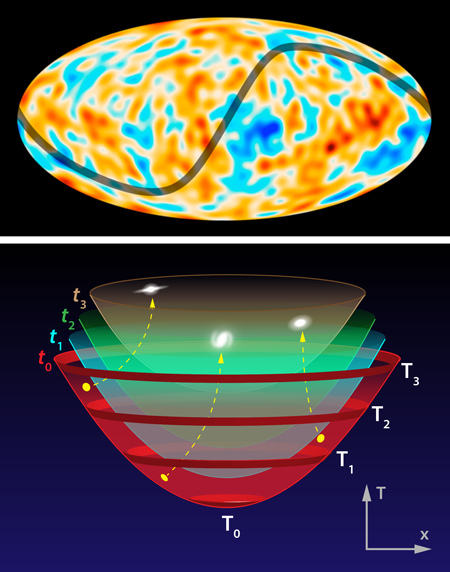
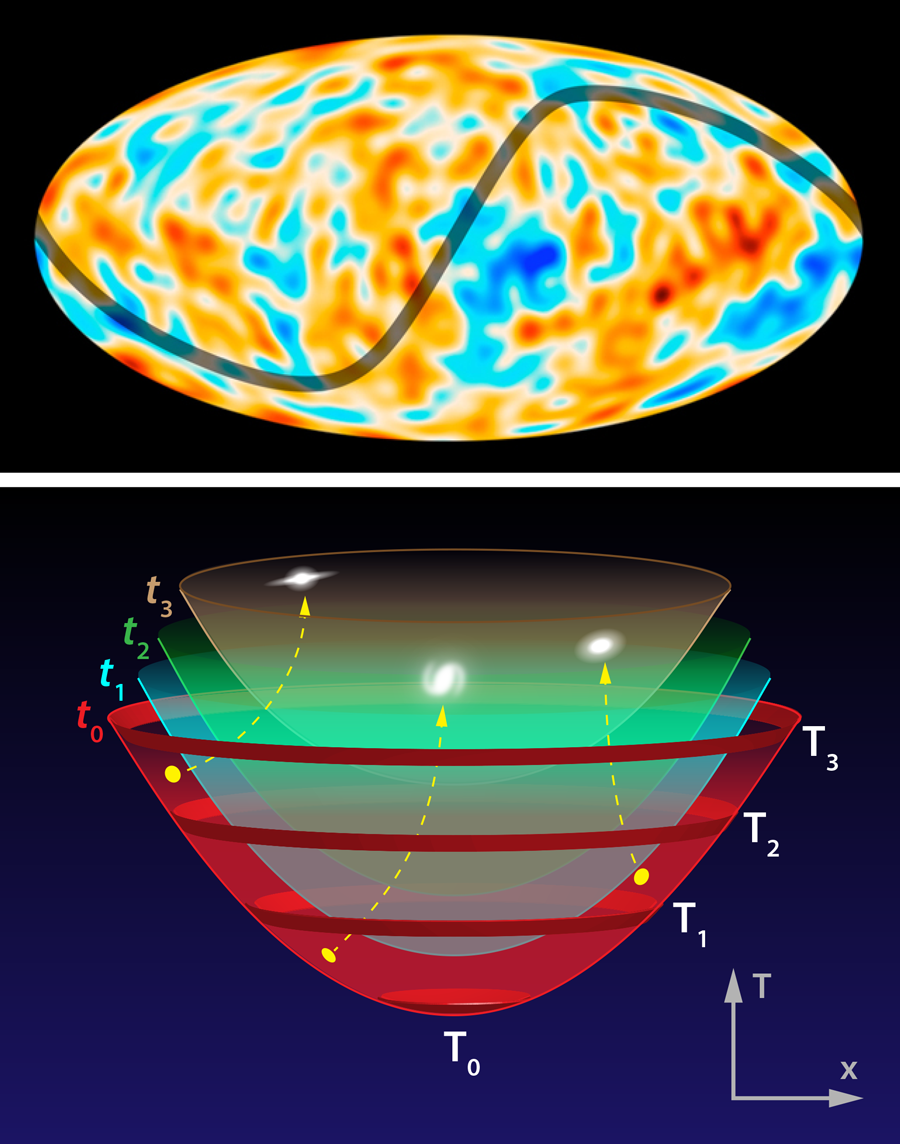
Cosmologists have learned much about our Universe from using the CMB as a cosmic temperature gauge. The spatial fluctuations in the microwave signal provide a window into the primordial density fluctuations that seeded galaxies and other cosmic structures. These fluctuations have been measured with exquisite precision by two recent space missions: the Planck satellite [3] and the Wilkinson Microwave Anisotropy Probe (WMAP) [4]. The data have confirmed many of the predictions of inflation, a hypothesized period of accelerated expansion occurring a tiny fraction of a second after the big bang. But some discrepancies, or “anomalies,” remain. In particular, the prediction of statistical homogeneity—the similarity of the distribution of primordial density fluctuations everywhere in space—has been called into question by the CMB measurements. Both the Planck Collaboration and the WMAP team have reported a difference in these fluctuations on two opposing hemispheres of the sky, roughly divided along the ecliptic plane (the plane defined by the orbit of the Earth around the Sun). The average temperature is the same in both hemispheres, but the variance (or spread) is roughly $10 %$ larger on one side of the sky compared to the other when the data are divided into patches that are $3^{\circ}$ wide or larger (see Fig. 1, top).

Before proceeding, it should be mentioned that the statistical significance of the result is still under debate. While the asymmetry is significant at the $≳ 3 σ$ level, some question whether it is simply a consequence of the “look-elsewhere” effect: i.e., we test for all kinds of anomalies in the CMB, and the investigated parameter space is so vast that it’s no surprise that, by chance, one of the parameters shows a positive result. Cosmological models make statistical predictions about the distribution of temperature fluctuations on an ensemble of CMB skies, but we have only one CMB sky to observe. Therefore, if the observed asymmetry is a statistical fluke, we are stuck with it because there is no way to increase the statistics on this particular measurement. But if the asymmetry is real and not just a statistical fluke, then it is extremely important. It may well be a remnant of the preinflationary Universe!

Several theorists have developed physical models for the asymmetry with the hope that these models will then make other predictions that can be tested empirically. These models must generate stronger temperature fluctuations on one side of the observable Universe, while still keeping the mean temperature the same on both sides to within $0.1 %$ . Moreover, the lopsided models must retain the very nearly Gaussian shape (to better than one part in $10^{4}$ ) in the distributions of primordial fluctuations at a particular angular scale.

One way to account for the asymmetry is to modify the inflationary model. The basic theory of inflation assumes that the rapid acceleration is driven by a quantum scalar field, called the inflaton. Perturbations in this field are typically thought to be the origin of the primordial fluctuations, but it is possible that the fluctuations came from a second scalar field, called the curvaton. Through this addition, the inflaton, which controls the total density of the Universe, can remain homogeneous, while a long-wavelength fluctuation in the curvaton can modulate the density-perturbation amplitude. In 2008, a group of theorists (myself included) developed a preliminary model in which a particular curvaton fluctuation could explain the CMB asymmetry [1].

Our model and those like it have simply pulled the curvaton fluctuation out of a hat, choosing its amplitude and wavelength so as to generate the observed asymmetry. By contrast, Liddle and Cortês suggest that the curvaton mode is directly related to the curvature scale in a marginally open Universe. An open, negatively curved Universe, where parallel lines diverge (like on a saddle), occurs when the total density is less than the so-called critical density, at which the gravitational potential energy of gravity matches the kinetic energy of expansion. Recent evidence suggests our Universe has a flat rather than curved geometry, but current measurements allow for a Universe in which the total density differs by as much as $1 %$ from the critical density. It is thus conceivable that the Universe appears flat but is actually curved with a characteristic radius that extends beyond our observable horizon by no more than an order of magnitude or so.

Liddle and Cortês propose that this superhorizon curvature radius sets the wavelength of the asymmetry-generating curvaton fluctuation. They then show that the amplitude of the curvaton fluctuation emerges naturally in “open inflation” models developed in the 1990s, in which our observable Universe forms like a bubble inside a larger metauniverse. This bubble is born, or nucleates, through a quantum tunneling event, in which the vacuum switches from one energy state to another. The bubble expands at a velocity that approaches the speed of light. One would not immediately guess that an open Universe, which has infinite volume, can be enclosed within a finite bubble. However, it is possible when one realizes that time is defined inside the bubble in a different way than outside (see Fig. 1, bottom). If we restrict ourselves to two space dimensions, then a specific time in our Universe is an infinite curved sheet, or hypersurface, in the spacetime of the larger metauniverse.

According to the open inflation model, the quantum tunneling event that gives birth to the bubble will also induce fluctuations in the bubble wall. These bubble-wall fluctuations imprint themselves in the curvaton fluctuations. Because of the curvature of an open Universe, the Fourier decomposition of these fluctuations is not the same as it would be in flat Euclidean space. For wavelengths larger than the curvature scale, the open-Universe generalization of Fourier modes must be augmented by a new set of “supercurvature” modes [5]. These supercurvature modes describe the density fluctuations that result from bubble-wall fluctuations [6].

Liddle and Cortês show that with suitable parameter choices, the open inflation model can generate a long-wavelength curvaton fluctuation with the amplitude required to account for the CMB asymmetry. The resulting Universe is consistent with the limits on the total density, as well as the Gaussianity in the fluctuation distribution.

The work of Liddle and Cortês is not complete, however. The asymmetry in their model is, like in Ref. [1], scale independent. That suggests that the two sides of the sky should have different density-fluctuation amplitudes for patches smaller than $3^{\circ}$ . But astronomical observations do not bear this out. Quasars, for example, appear in typically high-density regions that span about $1 / 100$ th of a degree, and their abundance differs by less than $1 %$ on both sides of the sky [7]. Additional work must be done to incorporate a scale-dependent asymmetry into these curvature-based models. One possibility is to have both the inflaton and the curvaton play roles in generating primordial perturbations [8,9].

Is there any way to test this new model? It makes many of the same predictions as previous models for Gaussianity, scale-dependence, and small-scale CMB temperature/polarization fluctuations [10]. Where it stands apart is in the prediction that the Universe should be very slightly open. The amount of curvature is small, but it might be detectable by the Planck collaboration as more and more of the data is analyzed. Otherwise, we may have to wait for a next-generation CMB satellite that would improve in sensitivity upon Planck.

References

A. L. Erickcek, M. Kamionkowski, and S. M. Carroll, “A Hemispherical Power Asymmetry From Inflation,” Phys. Rev. D 78, 123520 (2008)
A. R. Liddle and M. Cortês, “Cosmic Microwave Background Anomalies in an Open Universe,” Phys. Rev. Lett. 111, 111302 (2013)
P. A. R. Ade and et al., “Planck 2013 Results. XXIII. Isotropy and Statistics of the CMB,” arXiv:1303.5083
H. K. Eriksen, F. K. Hansen, A. J. Banday, K. M. Górski, and P. B. Lilje, “Asymmetries in the Cosmic Microwave Background Anisotropy Field,” Astrophys. J. 605, 14 (2004); “Erratum: “Asymmetries in the Cosmic Microwave Background Anisotropy Field (ApJ, 605, 14 [2004]),” Astrophys. J. 609, 1198 (2004)
D. H. Lyth and A. Woszczyna, “Large Scale Perturbations in the Open Universe,” Phys. Rev. D 52, 3338 (1995)
K. Yamamoto, M. Sasaki, and T. Tanaka, “Quantum Fluctuations And CMB Anisotropies In One-Bubble Open Inflation Models,” Phys. Rev. D 54, 5031 (1996)
C. M. Hirata, “Constraints on Cosmic Hemispherical Power Anomalies from Quasars,” J. Cosmol. Astropart. Phys. 2009, No. 9, 011 (2009)
A. L. Erickcek, C. M. Hirata, and M. Kamionkowski, “A Scale-Dependent Power Asymmetry From Isocurvature Perturbations,” Phys. Rev. D 80, 083507 (2009)
J. McDonald, “Isocurvature and Curvaton Perturbations with Red Power Spectrum and Large Hemispherical Asymmetry,” J. Cosmol. Astropart. Phys. 2013, No. 7, 043 (2013)
L. Dai, D. Jeong, M. Kamionkowski, and J. Chluba, “The Pesky Power Asymmetry,” Phys. Rev. D 87, 123005 (2013)

About the Author

Marc Kamionkowski is a theoretical physicist who specializes in cosmology. He earned a B.A. in physics (1987) at Washington University in St. Louis and a Ph.D. (1991) in physics at the University of Chicago, followed by postdoctoral study at the Institute for Advanced Study in Princeton (1991–1994) and a junior-faculty position at Columbia University (1994–1999). From 1999 to 2006 he was Professor, and from 2006 to 2011, the Robinson Professor, of Theoretical Physics and Astrophysics at the California Institute of Technology. In 2011 he joined the faculty at Johns Hopkins University as Professor of Physics and Astronomy.