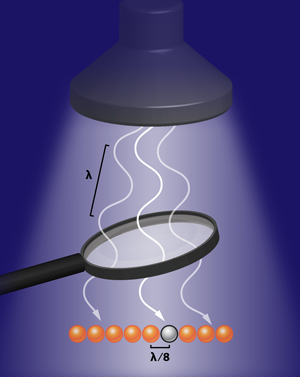
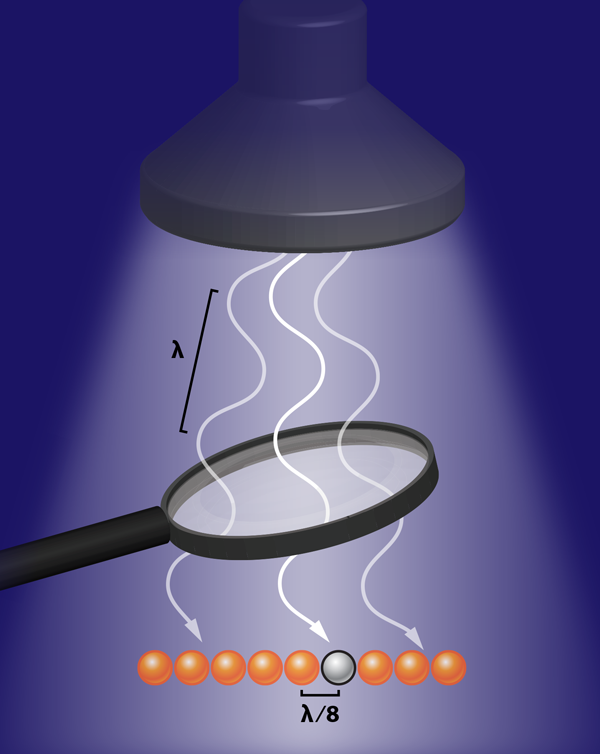
Localize and Conquer!

Mauro Paternostro

Viewpoint

Localize and Conquer!

Centre for Atomic, Molecular and Optical Physics, School of Mathematics and Physics, Queen's University Belfast, BT7 1NN Belfast, United Kingdom

September 11, 2013• Physics 6, 99

By illuminating atoms with two colors of light that drive interfering transitions, researchers selectively excite the atoms in a region much smaller than the light wavelength.

Figure caption — **Figure 1:** Carefully chosen illumination can excite atoms in a small region, without exciting atoms only one eighth of a wavelength away.

The ability to distinguish two objects in a microscope is fundamentally limited by optical diffraction, a principle first verified experimentally by Ernst Abbe [1]. This significantly affects our ability to optically target individual atoms and, in turn, limits the development of architectures for quantum information processing that depend on such precision targeting. Writing in Physical Review X, Jared Miles, of the University of Wisconsin at Madison, and his colleagues demonstrate experimentally a technique that, by cleverly exploiting the nonlinearity of a special light-matter interaction regime, allows them to create hyperfine excitations of ultracold $^{87} Rb$ atoms only within tiny spatial regions that are eight times smaller than the wavelength of the light used to illuminate them [2].

For a human-scale analogy, think of your mobile phone. Leave aside the fancy design and the tens of accessories that make these objects so useful. What remains is one basic property, which is central to the topic of this commentary: they are tiny. So much so that it is likely that most of us have thought, at least once, that the fingers of an average adult are definitely too big to hit only the button that we are interested in! Now, let us replace your fingers with your favorite imaging device (your camera, a telescope, or a microscope) and two nearby cell-phone buttons with two small objects that you would like to view. How distant should the two objects be in order for your camera to be able to fully resolve them? The answer is provided by a fundamental law of nature, the “diffraction-limit principle,” which limits such distance to half the wavelength of the light used to image the two objects.

The diffraction-limit principle has more far-reaching consequences than determining the resolution of a commercial camera, in particular, when quantum mechanics is involved. While remaining valid for objects of all length scales, the diffraction limit embodies a fundamental bound to our ability to resolve spatially separated microscopic or submicroscopic systems. In turn, this has significantly slowed the practical development of quantum technologies based on the manipulation of individual neutral atoms.

Let us address this point in a bit more detail. Among the architectures proposed so far for a quantum computing device [3], those based on trapped atomic systems (such as neutral atoms, for instance) are very promising because of their scalability to many elements, the possibility to build controllable and efficient data registers, and (for ultracold atomic samples) their intrinsic robustness to noise. Yet a key step in manipulating information in such a system is establishing strong interactions between neighboring atoms, which typically require interatomic distances below the diffraction limit to achieve strong coupling. Therefore, to both manipulate a pair of atoms and read out their state individually, one has to compromise on their separation and, in turn, reduce the speed and quality of the resulting two-atom evolution.

Addressing individual atoms is also essential for efficient initialization of the elements of a quantum computer and the readout of the computational result. For instance, in the so-called “one-way model” for quantum computation [4], information encoded in a large register of neutral atoms can be processed in any chosen way by means of suitable state initialization and the right sequence of single-atom measurements, both of which require addressing single atoms. The basic building blocks of this model have been demonstrated in a small-scale lattice of ultracold atoms [5]. However, its development, scaling, and employment for computational purposes have been hindered by the required distance between the atoms, which is too short for them to be individually addressed by optical means.

Building on a theoretical proposal by Agarwal and Kapale [6] and Gorshkov et al. [7], Miles and colleagues show experimentally that a clever use of the nonlinear regime of interaction between light and an atomic sample known as “electromagnetically induced transparency” (EIT) [8] is indeed effective in achieving subwavelength atomic localization.

In a nutshell, the idea works as follows: consider atoms with three energy levels that have a so-called $Λ$ configuration, which comprises two low-lying levels (which we name $1$ and $2$ ) and an excited one. The transition from level $1$ to the excited level is driven at a rate $Ω_{p}$ , proportional to the strength of a “probe” laser field, while the transition from level $2$ to the excited state is driven at a rate $Ω_{c}$ by a second “coupling” field. Both fields are necessary: without the coupling field, the probe would be absorbed by the atomic medium. However, owing to destructive quantum interference between the two transitions, when the coupling field is also present, the medium can be made fully transparent to any radiation within a (narrow) width of frequencies, thus establishing the EIT regime. In such conditions, the atoms are driven into a so-called “dark state” consisting of a quantum coherent superposition of levels $1$ and $2$ only, and the excited atomic state completely disappears from the dynamical equations. In the dark state, the probability that a single atom occupies level $2$ depends on the ratio $| Ω_{c} / Ω_{p} |$ : the smaller this ratio, the higher the chance of finding the atoms in level $2$ .

If the coupling light, and thus $Ω_{c}$ , is now made to vary with position, the dark state itself becomes sensitive to the local intensity of the coupling field. The trick is now evident: it is enough to employ a standing-wave coupling field to localize the population of level $2$ near the nodes where $Ω_{c}$ vanishes. By using a weak probe field, the region where the coupling field is even weaker can be made much shorter than the wavelength of the light. In their experiment, Miles and colleagues used a $30$ milliwatt coupling field resonant with the $780$ nanometer $D_{2}$ transition of $^{87} Rb$ and, by implementing the method sketched above, have been able to localize the atoms prepared in the dark level $2$ within a region as small as $129$ nanometers (see Fig.1). They verified this size by measuring how far the intensity minimum needed to be moved before it encountered unexcited atoms.

The creation of the dark state relies only on collective manipulation of the atoms in a sample, and it can be achieved by means of adiabatic preparation techniques [7] that make it inherently robust against light intensity fluctuations. The group at Madison is now working towards an even better localization, aiming at confinement of the order of $10$ nanometers, which might be possible by cranking up the field intensity to $100$ milliwatts. This requires considerable technical progress because such strong laser fields break down the three-level approximation upon which the whole scheme is based. Yet the outlook is promising, and the team aims at creating single and two-qubit gates with nanometer spatial resolution, as suggested by Gorshkov et al. [7]

References

E. Abbe, “A Contribution to the Theory of the Microscope and the Nature of Microscopic Vision,” Proc. Bristol Nat. Soc. 1, 200 (1874)
J. A. Miles, Z. J. Simmons, and D. D. Yavuz, “Subwavelength Localization of Atomic Excitation Using Electromagnetically Induced Transparency,” Phys. Rev. X 3, 031014 (2013)
M. A. Nielsen and I. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000)[Amazon][WorldCat]
H. Briegel, D. E. Browne, W. Dür, R. Raussendorf, and M. Van den Nest, “Measurement-Based Quantum Computation,” Nature Phys. 5, 19 (2009)
O. Mandel, M. Greiner, A. Widera, T. Rom, T. W. Hansch, and I. Bloch, “Controlled Collisions for Multi-Particle Entanglement of Optically Trapped Atoms,” Nature 425, 937 (2003)
G. S. Agarwal, and K. T. Kapale, “Subwavelength Atom Localization via Coherent Population Trapping,” J. Phys. B 39, 3437 (2006)
A. V. Gorshkov, L. Jiang, M. Greiner, P. Zoller, and M. D. Lukin, “Coherent Quantum Optical Control with Subwavelength Resolution,” Phys. Rev. Lett. 100, 093005 (2008)
M. Fleischhauer, A. Imamoglu, and J. P. Marangos, “Electromagnetically Induced Transparency: Optics in Coherent Media,” Rev. Mod. Phys. 77, 633 (2005)

About the Author

Mauro Paternostro received his Ph.D. from Queen’s University Belfast (QUB) for his work on theoretical quantum information processing. After having been a research fellow at the Institute for Quantum Optics and Quantum Information, University of Vienna, and at QUB, he was awarded in 2008 an EPSRC Career Acceleration Fellowship and appointed Lecturer at QUB, where he is currently a Reader. He co-leads the Quantum Technology group at QUB, where he works on foundations of quantum mechanics and quantum information processing. He is strongly interested and has significantly contributed to quantum optomechanics and the coherent manipulation of open mesoscopic quantum systems. Honors include a Leverhulme Trust Early Career Fellowship and an Alexander von Humboldt Fellowship for experienced researchers.