Particle Scattering Simplified

Lance J. Dixon

Viewpoint

Particle Scattering Simplified

SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94309, USA

October 20, 2014• Physics 7, 107

A new formula for the scattering of massless particles may simplify predictions and analyses of LHC experiments and shed new light on quantum gravity theories.

Figure caption — **Figure 1:** (Top) To model LHC and other particle physics experiments, researchers use Feynman diagrams—representing the interactions of subatomic particles. But calculating all possible Feynman diagrams is not feasible and the exact probabilities are approximated using perturbation theory. A first-order approximation is given by tree-level diagrams (treelike diagrams without any closed loops), while improved accuracy is obtained by including higher-order approximations (one loop, two loops, etc.). The sketched diagrams refer to the scattering of a quark ( $q$ ) and a gluon ( $g$ ) into a $W$ boson (carrier of the weak force) and another quark ( $q^{'}$ ). (Bottom) Cachazo, He, and Yuan [1] have derived two simplified formulas describing, with tree-level precision, the scattering matrix of $n$ gluons ( $A_{n}$ ) and gravitons ( $M_{n}$ ). The two formulas are almost identical, except for the factor highlighted by a red box, which is squared for the case of gravitons. This similarity might shed light on the quantum nature of gravity.

Virtually everything we have learned in the past century about the rules governing the behavior of subatomic particles has been gleaned from the debris of particle collisions at a series of increasingly more powerful accelerators. From Rutherford’s gold-foil experiment revealing the atomic nucleus, to the discovery of the Higgs boson at the Large Hadron Collider (LHC), the observation and interpretation of quantum scattering processes have been vital to the progress of particle physics.

Experiments such as those carried out at the LHC to study the Higgs boson or search for new, non-standard-model particles present enormous challenges. For instance, only about one in a trillion proton-proton collisions produces a detectable Higgs boson. Much more frequent are collisions in which more mundane standard-model particles are produced—a background that must be subtracted before claiming a discovery. Theory is thus crucial to plan, guide, and interpret these experiments.

To describe these processes, theorists calculate so-called “scattering amplitudes”: the complex numbers that, in quantum mechanics, get squared to provide probabilities for incoming particles to scatter into outgoing ones. These calculations can be prohibitively complicated, but a new—potentially simplifying—formula for finding the scattering amplitude of gluons (the carriers of the strong interaction between quarks) has now been presented by Freddy Cachazo, Song He, and Ellis Yuan (CHY) at the Perimeter Institute, the University of Waterloo, both in Canada, and the Institute for Advanced Study, New Jersey [1]. The work also derives a similar formula for gravitons (the hypothetical carriers of the gravitational force), which might help shed new light on quantum gravity theories.

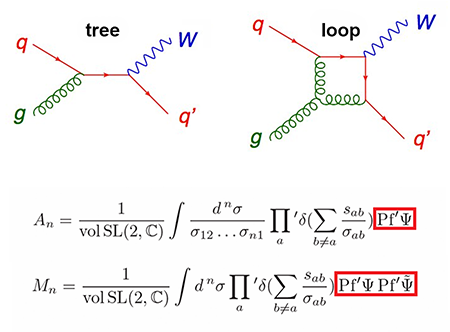
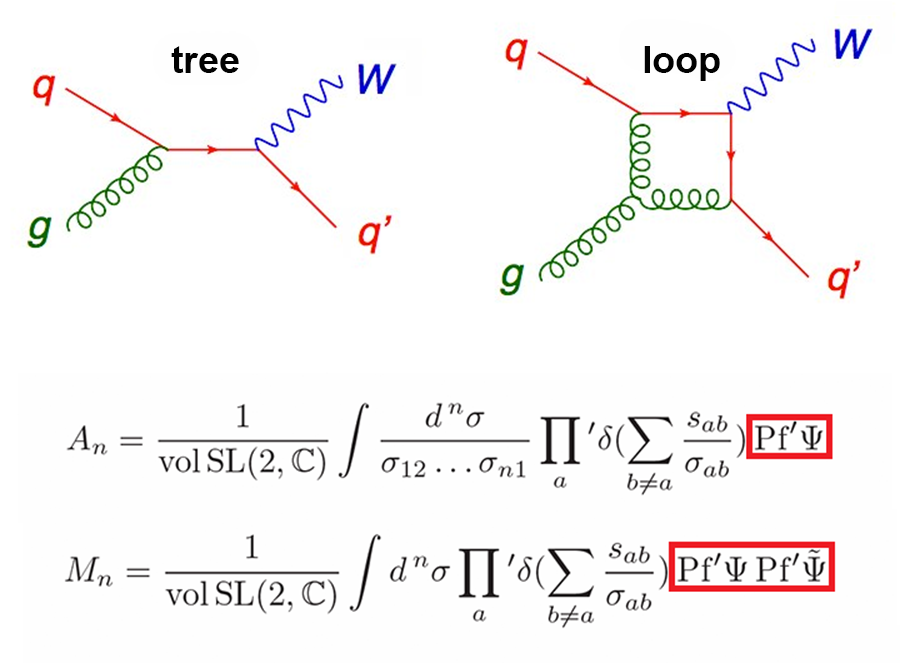
The challenges involved in providing accurate theoretical predictions for LHC experiments are daunting. Theorists are faced with working through thousands, or even hundreds of thousands, of Feynman diagrams—representations of the mathematical expressions describing the interactions of subatomic particles (see Fig. 1, top). The contributions of all diagrams to the scattering amplitude are summed up and then squared to get the probability of a given outcome. This process must be repeated for all relevant energies and angles of the scattered particles.

But calculating all possible Feynman diagrams is not feasible. Using perturbation theory, the exact probabilities can be expanded as a power series in a small parameter (for QCD, the coupling constant $α_{S}$ ). Higher orders in the perturbative expansion give more accurate predictions. The leading term in the expansion is called tree level because one uses Feynman diagrams with a treelike topology, with no closed loops. The next approximations include one-loop corrections (all diagrams with one closed loop), then two loops, etc., (see Fig 1, top). Even with the aid of powerful computers, the computations are often still impractically slow for processes with many final-state particles, especially when loop-level precision is required (as turns out to be the case for Higgs production at the LHC, for which the leading approximation is wrong by a factor of $2$ ).

Thirty years ago, theorists began to realize that Feynman diagrams might not be the best way to compute scattering amplitudes. Their results were often very simple and contained striking recurring patterns that were not immediately evident in a Feynman-diagram representation. Since then, a growing band of “amplitude explorers” has been uncovering further patterns, using them to find new ways to compute ever more complex amplitudes. (For more on this story, see my 2013 post on Sean Carroll’s blog.) The CHY formula falls squarely in this line of research. Describing the scattering of an arbitrary number $n$ of gluons or gravitons, it reveals a number of new features.

One surprising feature is how the CHY formula is related to string theory. In string theory, particles are replaced by one-dimensional strings. As they scatter, strings trace out many possible two-dimensional surfaces—to calculate the probability of a certain outcome, one has to sum over all possible surfaces. A similarity with particle scattering emerges at low energies: Strings can vibrate in various modes, with high harmonics behaving like ultraheavy-mass particles, and the lowest harmonics acting like massless particles (such as gluons) and scattering just like gluons. The low-energy limit of string theory (when there is not sufficient energy to excite ultraheavy-particle-like resonances) has been used for many years to understand features of particle scattering.

The surprising thing is that the CHY formula looks like the scattering of strings at very high (above the Planck scale) energies. In 1987, Gross and Mende [2] showed that also in a high-energy limit, string scattering simplifies vastly. The scattering is classical, and as a consequence, the two-dimensional surfaces do not fluctuate and are pinned to discrete locations. CHY’s formula for particle scattering contains exactly these pinned locations. This correspondence of particle scattering with high-energy string scattering is profound and mysterious and may provide another avenue by which tools from string theory could help tackle particle scattering problems.

The CHY formula has already triggered further work: inspired by its connection to high-energy string scattering, Mason and Skinner have recently constructed a new “ambitwistor” string theory [3]. This theory is an extension of Witten’s “twistor” string theory [4], based on the idea of doing string theory in twistor space (a spacetime representation introduced by Penrose in the 1960s as a possible path to quantum gravity [5]). Both twistor and ambitwistor string theories are different from the usual string theory in lacking ultraheavy stringy resonances. While they both reproduce gluon scattering amplitudes at tree level (at all energies), only the more recent ambitwistor string leads to the CHY formula. Witten’s twistor string theory has led to many new perspectives on particle scattering. The new ambitwistor string is likely to have a similar impact.

What are the other implications of CHY’s formulas? For applications to LHC processes, the crucial question is whether they can be extended to loop-level amplitudes. A variety of efficient methods for tree amplitudes already exists; the real computational challenges begin at one loop, getting more severe at two loops. The formalism of ambitwistor strings might help extend CHY’s formula to the loop level: one-loop amplitudes have already been computed for ambitwistor strings [6]. But it still has to be determined whether ambitwistor string theory can really compute loop amplitudes for gluons. Should loop-level extensions succeed, the theory could address LHC processes that are currently beyond the state of the art. For example, the ongoing search for supersymmetric particles at the LHC, requiring an excellent understanding of a broad array of processes with complicated final states, would greatly benefit from loop-level extensions.

But the CHY relations might have a more fundamental impact on quantum gravity. While the force carriers in the standard model, such as gluons, have spin 1, the graviton has spin 2. This difference makes gravity fundamentally different and its quantum nature more elusive. Making gravity look more “gluonic” could help us understand its quantum properties. CHY’s formula for graviton scattering is almost identical to the gluon formula, with the main difference that one factor in the formula is squared (see Fig. 1, bottom). In 2008, Bern, Carrasco, and Johansson (BCJ) [7] found a square-type relation for particle scattering. BCJ formulas have been derived, in special cases, for up to four loops [8,9], contributing to test certain aspects of quantum gravity (see 17 August 2009 Viewpoint). However, there is still no general recipe for extending these formulas to the necessary loop levels. Perhaps the new CHY relations, by making BCJ’s squaring property manifest within a stringlike formula, could lead to a strategy for finding BCJ solutions at all loop orders, making them suitable for tackling quantum gravity.

This research is published in Physical Review Letters.

References

Freddy Cachazo, Song He, and Ellis Ye Yuan, “Scattering of Massless Particles in Arbitrary Dimensions,” Phys. Rev. Lett. 113, 171601 (2014)
D. J. Gross and P. F. Mende, “The High-Energy Behavior of String Scattering Amplitudes,” Phys. Lett. B 197, 129 (1987); “String Theory Beyond the Planck Scale,” Nucl. Phys. B 303, 407 (1988)
L. Mason and D. Skinner, “Ambitwistor Strings and the Scattering Equations,” J. High Energy Phys. 1407, 048 (2014)
E. Witten, “Perturbative Gauge Theory as a String Theory in Twistor Space,” Commun. Math. Phys. 252, 189 (2004)
R. Penrose, “Twistor Algebra,” J. Math. Phys. 8, 345 (1967)
T. Adamo, E. Casali, and D. Skinner, “Ambitwistor Strings and the Scattering Equations at One Loop,” J. High Energy Phys. 1404, 104 (2014)
Z. Bern, J. J. M. Carrasco, and H. Johansson, “New Relations for Gauge-Theory Amplitudes,” Phys. Rev. D 78, 085011 (2008)
Z. Bern, J. J. M. Carrasco, and H. Johansson, “Perturbative Quantum Gravity as a Double Copy of Gauge Theory,” Phys. Rev. Lett. 105, 061602 (2010)
Z. Bern, J. J. M. Carrasco, L. J. Dixon, H. Johansson, and R. Roiban, “Simplifying Multiloop Integrands and Ultraviolet Divergences of Gauge Theory and Gravity Amplitudes,” Phys. Rev. D 85, 105014 (2012); Z. Bern, S. Davies, and T. Dennen, “Enhanced Ultraviolet Cancellations in $N = 5$ Supergravity at Four Loop,” arXiv:1409.3089

About the Author

Lance Dixon is professor and chair of the Particle Physics and Astrophysics Department at SLAC National Accelerator Laboratory, Stanford University http://www.slac.stanford.edu/~lance/. He received his Ph.D. in 1986 from Princeton University and has been at SLAC since 1988. He studies elementary particle theory and its applications to collider physics. In 2008 he was recognized as an Outstanding Referee by the American Physical Society, and in 2014 he was a co-recipient of the J. J. Sakurai Prize of the APS for his work on scattering amplitudes.