Arrow of Time Emerges in a Gravitational System
The fundamental laws of physics, we believe, do not depend on the direction of time. Why, then, is the future so different from the past? The origin of this “arrow of time” has puzzled physicists and philosophers for more than a century, and it remains one of the fundamental conceptual problems of modern physics [1]. Although a preferred direction of time can occur in models of physical systems, this typically happens only if one inserts very special initial conditions. Julian Barbour at the University of Oxford and his colleagues [2] have now shown this tinkering isn’t necessary to produce an arrow of time in a system of masses interacting via Newtonian gravity. They demonstrate that the evolution of this surprisingly simple system almost always contains a unique moment of lowest “complexity,” a point they identify as a “past” from which two distinct (and more complex) “futures” emerge.
The work of Barbour and his colleagues is the latest in a long history of attempts to explain the arrow of time. One possibility, of course, is that we don’t know the right laws of physics—perhaps the correct fundamental laws do determine a preferred direction of time [3]. Alternatively, if the laws of nature do not pick out a preferred “future,” perhaps boundary conditions do. For example, most cosmological models assume, explicitly or implicitly, that the big bang was a moment of exceptionally low entropy.
Indeed, most physicists accept the view that the direction of time is the same as the direction of increasing entropy. But this is, at best, an incomplete picture, failing to explain why there should have been a rare condition of low entropy in the past. More than a century ago, Boltzmann suggested that our visible Universe might merely be a temporary, low-entropy statistical fluctuation, affecting a small portion of a much larger equilibrium system [4]. In that case, the direction of time would simply be the one that takes us back towards equilibrium. But most contemporary physicists find this explanation unsatisfying: a random fluctuation containing “us” would have been far more likely to produce a single galaxy, a planet, or just a “brain” rather than a whole universe [5,6]. Moreover, according to the “Loschmidt irreversibility paradox,” if one posits such a moment of low entropy, entropy should increase both to the future and to the past, giving two separate arrows of time [7].
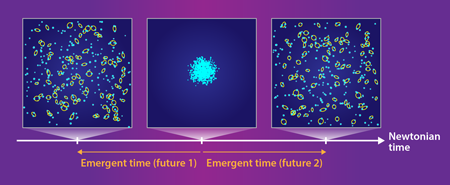
In their gravitational model, Barbour and his colleagues find a state of “low complexity” that is analogous to Boltzmann’s low-entropy fluctuation. But in their case, no rare statistical fluctuation is necessary to explain this state; instead, it arises naturally out of simple physical laws that have no explicit dependence on the direction of time. The authors study one of the simplest possible systems: a collection of N point particles interacting through Newtonian gravity. Their only assumptions are that the total energy (potential plus kinetic) and the total angular momentum of the system are zero. From earlier numerical simulations and analytic analysis, it is known that in the distant future, such a system tends to break up into weakly interacting subsystems—typically, pairs of masses in Keplerian orbits [8]. Starting with such a dispersed system and running time backwards, one might expect that it would coalesce in the past into a state of high density. Barbour and his coauthors show analytically that this expectation is right: for almost every initial configuration of masses, there is a unique moment of minimum size and maximum uniformity. From this point, the system expands outward, approximately symmetrically in both directions of time (Fig. 1). The system is therefore globally symmetric in time, as the equations dictate, and yet has a local arrow of time.
As a key step in their argument, the authors analyze the evolution of the masses in “shape space,” a space of observables that describe the shape of the system but are independent of its size and orientation. Three bodies, for instance, form a triangle, and their shape space is the space of similar triangles. Shape space contains a natural dimensionless measure of complexity, denoted CS, which is determined by the moment of inertia and the total Newtonian gravitational potential. CS describes the degree of nonuniformity and clustering; it has a minimum at the moment of minimum size and grows approximately monotonically from that minimum in both directions of time. Barbour and his colleagues provide a fairly simple and intuitive explanation for this behavior by showing that the dynamics of the N-body system in shape space has an effective friction term, which provides a sort of dissipation even though the underlying equations of motion are symmetric in time.
The idea of time proceeding in two directions, towards two futures, from a moment of minimum complexity is not itself new. It has appeared, for example, in cosmological models of eternal inflation [9]. But the emergence of this behavior in a system as simple as the one Barbour and his colleagues consider is unexpected. The constraints of vanishing energy and angular momentum were based on a Machian philosophical view; namely, that only relational observables should be relevant to physics. But these choices also appear to match our Universe; vanishing energy, for instance, is an indication of spatial flatness. It is worth emphasizing, however, that the model in this paper is Newtonian—it is not yet clear whether it can be extended to a more realistic general relativistic description of gravity, though the authors suggest this might be possible by using shape dynamics [10], a modified scale-invariant form of general relativity.
Have Barbour and his colleagues solved the problem of the arrow of time? Probably not yet. We’re still left with the mystery that the arrows of time we see in different physical phenomena all point in the same direction. Electromagnetic waves are retarded, not advanced; radioactive nuclei decay, they don’t reassemble; gravitating systems clump, they don’t disperse; we remember the past, not the future. A good deal of work would be required to show that these disparate arrows all match the direction determined from a purely gravitational model.
Nevertheless, the results of Barbour and his colleagues provide an intriguing new viewpoint. Standard approaches to the arrow of time typically require a rare statistical fluctuation, or, often, the smuggling in of assumptions about initial conditions. Their work offers evidence that ordinary gravitational dynamics may itself be enough to produce the simple “initial” point that can give time a direction.
References
- H. D. Zeh, The Physical Basis of the Direction of Time (Springer-Verlag, Berlin, 2007)[Amazon][WorldCat]
- Julian Barbour, Tim Koslowski, and Flavio Mercati, “Identification of a Gravitational Arrow of Time,” Phys. Rev. Lett. 113, 181101 (2014)
- The violation of time-reversal invariance by the weak interactions doesn’t count, since the interactions are still charge-parity-time (CPT) invariant
- L. Boltzmann, “On Certain Questions of the Theory of Gases,” Nature 51, 413 (1895)
- R. Feynman, The Character of Physical Law (MIT Unversity Press, Cambridge, 1967)[Amazon][WorldCat]
- A. Albrecht, “Cosmic Inflation and the Arrow of Time,” arXiv:astro-ph/0210527
- J. Loschmidt, “Uber den Zustand des Warmegleichgewichtes eines Systems von Korpern mit Rücksicht auf die Schwerkraft,” Wien. Ber. 73, 128 (1876)
- C. Marchal and D. Saari, “On the Final Evolution of the N-body Problem,” J. Diff. Eq. 20, 150 (1976)
- S. M. Carroll and J. Chen, “Spontaneous Inflation and the Origin of the Arrow of Time,” arXiv:hep-th/0410270
- H. Gomes, S. Gryb, and T. Koslowski, “Einstein Gravity as a 3D Conformally Invariant Theory,” Class. Quantum Grav. 28, 045005 (2011)