Trapped Ions Make Impeccable Qubits

Jungsang Kim

Viewpoint

Trapped Ions Make Impeccable Qubits

Department of Electrical and Computer Engineering, Duke University, Durham, NC 27708, USA

November 24, 2014• Physics 7, 119

Qubits based on trapped ions can be prepared and manipulated with record-breaking accuracy, offering a promising scalable platform for quantum computing.

Figure caption — **Figure 1:** Qubits made of a trapped $^{43} {Ca}^{+}$ ion. RF and dc electrodes provide a trapping field for the ions, which are cooled by laser beams (blue) to microkelvin temperatures. A combination of laser pumping and microwave signals can deterministically prepare the qubit in a $| 0 〉$ or $| 1 〉$ state, and the state can be read out by monitoring its fluorescence (only $| 1 〉$ states result in the fluorescence, similar to that shown in the inset). Further logical gate operations can be carried out by applying various combinations of microwave pulses. The scheme yields preparation and readout errors of less than $0.07 %$ and logic-gate errors of less than $10^{- 6}$ .

The realization, two decades ago, that quantum mechanics can be a powerful resource to speed up important computational tasks [1] led to intense research efforts to find adequate physical systems for quantum computation. One of the hurdles to a viable technology is the requirement to prepare, manipulate, and measure quantum bits (qubits) with near perfect accuracy: Imperfect control leads to errors that can accumulate over the computation process. Techniques like quantum error correction and fault-tolerant designs can, in principle, overcome these errors. But these strategies can be successful only if the error probabilities are lower than a threshold value. They also increase the complexity of the required quantum hardware, since they require additional qubits. Recent calculations [2] suggest that an error probability of less than $1 %$ would enable fault-tolerant codes, and that lower error probabilities dramatically decrease the number of qubits required for such codes.

The quality of qubit manipulation in a number of physical systems has dramatically improved in the past few years [3,4], raising hopes that a quantum computer, at a large enough scale to carry out meaningful computations, might be within reach. Now, Thomas Harty at the University of Oxford, UK, and colleagues [5] are reporting an important contribution to this goal with the demonstration that qubits consisting of trapped $^{43} {Ca}^{+}$ ions can be manipulated with record high fidelities (in quantum information theory, fidelity is a measure of the “closeness” of two quantum states). Their experiments suggest trapped-ion schemes could potentially provide the basic fundamental building blocks of a universal quantum computer.

Trapped atomic ions are one of the leading candidate systems to construct a robust quantum computer: they provide a stable and well-isolated quantum system and the strong Coulomb forces between the ions can be used to realize logical gate operations by coupling different qubits. In the last decade, researchers have demonstrated trapped-ion qubits with long coherence times [6], high-fidelity state preparation and readout [7], and single- and two-qubit logic gate operations with low error rates [3,8]. Yet each of these properties was demonstrated individually in different systems. The work of Harty and colleagues now poses a combined improvement on all of these fronts in a single experimental system.

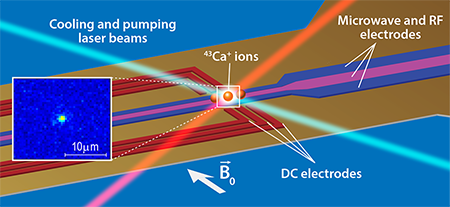
In the authors’ scheme (see Fig. 1), a $^{43} {Ca}^{+}$ ion is confined by radiofrequency electric fields (a so-called “Paul trap”) on the surface of a sapphire substrate. Electrodes connected to the structure provide the signals necessary for trapping the ions and driving changes to the qubit states. The choice of the $^{43} {Ca}^{+}$ was crucial to the authors’ results: With a modest applied magnetic field ( $146$ gauss), the energy-level separation between the two hyperfine ground-state sublevels of the ion is sufficiently large to become insensitive to small magnetic field fluctuations, abundant in a laboratory environment, that affected the performance of previous trapped-ion schemes. The two hyperfine states of $^{43} {Ca}^{+}$ are thus ideal for representing the $| 0 〉$ and $| 1 〉$ qubit states (analogous to “ $0$ ” and “ $1$ ” in classical computing systems). A crucial property of a qubit is its coherence time (how long a quantum superposition of $| 0 〉$ and $| 1 〉$ states can be maintained). Unlike previous experiments with $^{40} {Ca}^{+}$ ions, here the hyperfine levels’ stability led to a measured coherence time of about $50$ seconds, marking a record for an atomic-ion qubit unshielded from fluctuating background magnetic fields.

To “prepare” the ion’s electron in a well-defined initial state, the authors use laser-pumping techniques that are well established for atomic systems. They first drive the electron to one of the hyperfine ground states of $^{43} {Ca}^{+}$ by shining a laser beam resonant with the atomic transition. From such a ground state, either the $| 0 〉$ or the $| 1 〉$ qubit state can be prepared using adequate microwave pulses applied to the ion through the on-chip microwave electrodes. In order to “read” the qubit states with high accuracy, the researchers exploit the fact that, when excited by a sequence of optical pulses, only one of the two qubit states would fluoresce. If the qubit was a $| 0 〉$ , optical excitation would bring it to a metastable state, which would not emit fluorescence upon application of a resonant laser beam. If instead the qubit was a $| 1 〉$ , the ion would not be transferred to the metastable state and resonant laser excitation would induce a fluorescence signal that can be imaged by a photon detector (see inset of Fig. 1). The authors repeated the qubit preparation and readout $150, 000$ times, reporting an average error rate of only $0.07 %$ .

To carry out logic-gate operations, the qubit state can be coherently manipulated by exposing the ion to a 3.2-gigahertz microwave pulse that toggles the qubit between its two levels. The authors show that the phase and duration of the microwave pulse can be precisely controlled to achieve the desired operations with near-perfect accuracy. Following a gate-testing protocol known as “randomized benchmarking,” the authors use the microwave electrodes to drive a long sequence of single-qubit gate operations, comparing the final qubit state with the expected outcome. They report an average error probability of $1 \times 10^{- 6}$ for a single-qubit gate operation, which is more than an order of magnitude better than previous demonstrations [8]. These results, combined with the high-fidelity two-qubit gate operation reported by the same authors in a separate paper [9], make a convincing demonstration of a universal set of qubit operations that represent a high-fidelity record in any physical platform so far investigated.

The reported combined accuracy in preparation, readout, and logical-gate operation satisfies the important benchmark of an error rate lower than the $1 %$ threshold, beating it by over an order of magnitude. Along with the impressive recent progress made in superconducting qubits [4], these results show that scientists seem to be homing in on achieving the qubit quality necessary for constructing and operating a large-scale, fault-tolerant quantum information processing system. The next set of challenges lies in the ability to integrate all of these functionalities into a single experimental setup and to scale up the system to a larger number of qubits [10]. At such a pace of technology development, quantum computers, which seemed a remote possibility only a decade ago, might become a reality sooner than most of us anticipated.

This research is published in Physical Review Letters.

References

P. W. Shor, “Algorithms for Quantum Computation: Discrete Logarithms and Factoring,” in Proceedings of the 35th Annual Symposium on Foundations of Computer Science (IEEE Computer Society Press, Los Alamitos, 1994); L. K. Grover, “Quantum Mechanics Helps in Searching for a Needle in a Haystack,” Phys. Rev. Lett. 79, 325 (1997)
A. G. Fowler, M. Mariantoni, J. M. Martinis, and A. N. Cleland, “Towards Practical Large-Scale Quantum Computation,” Phys. Rev. A 86, 032324 (2012); A. M. Steane, “Overhead And Noise Threshold of Fault-Tolerant Quantum Error Correction,” 68, 042322 (2003)
J. Benhelm, G. Kirchmair, C. F. Roos, and R. Blatt, “Towards Fault-Tolerant Quantum Computing with Trapped Ions,” Nature Phys. 4, 463 (2008)
R. Barends et al., “Superconducting Quantum Circuits at the Surface Code Threshold for Fault Tolerance,” Nature 508, 500 (2014)
T. P. Harty, D. T. C. Allcock, C. J. Ballance, L. Guidoni, H. A. Janacek, N. M. Linke, D. N. Stacey, and D. M. Lucas, “High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit,” Phys. Rev. Lett. 113, 220501 (2014)
C. Langer et al., “Long-Lived Qubit Memory Using Atomic Ions,” Phys. Rev. Lett. 95, 060502 (2005)
A. H. Myerson, D. J. Szwer, S. C. Webster, D. T. C. Allcock, M. J. Curtis, G. Imreh, J. A. Sherman, D. N. Stacey, A. M. Steane, and D. M. Lucas, “High-Fidelity Readout of Trapped-Ion Qubits,” Phys. Rev. Lett. 100, 200502 (2008); R. Noek, G. Vrijsen, D. Gaultney, E. Mount, T. Kim, P. Maunz, and J. Kim, “High Speed, High Fidelity Detection of an Atomic Hyperfine Qubit,” Opt. Lett. 38, 4735 (2013)
K. R. Brown, A. C. Wilson, Y. Colombe, C. Ospelkaus, A. M. Meier, E. Knill, D. Leibfried, and D. J. Wineland, “Single-Qubit-Gate Error below $10^{- 4}$ in a Trapped Ion,” Phys. Rev. A 84, 030303 (2011)
C. J. Balance, T. P. Harty, N. M. Linke, and D. M. Lucas, “High-Fidelity Two-Qubit Quantum Logic Gate Using Trapped $^{43}$ Ca $^{+}$ Ions,”arXiv:1406.5473v1 (2014)
C. Monroe and J. Kim, “Scaling the Ion Trap Quantum Processor,” Science 339, 1164 (2013)

About the Author

Jungsang Kim is a professor of Electrical and Computer Engineering, Physics, and Computer Science at Duke University in North Carolina. He leads the Multifunctional Integrated Systems Technology group, concentrating on experimental implementation of novel computing and sensing systems such as scalable modular quantum computers and quantum networks using trapped ions, high-performance single-photon detectors and free-space quantum key distribution systems, and gigapixel-scale cameras. Jungsang Kim received his Ph.D. in physics from Stanford University and worked as a Member of Technical Staff and a Technical Manager at Bell Laboratories in Murray Hill, New Jersey.