How Rocks Break
The cracking of stone and rock can bring down a bridge, a cliff face, or—if it happens deep in the earth during an earthquake—an entire city. In Physical Review Letters and Physical Review E, a team of researchers presents a model of fracture at the microscale in a porous material such as sedimentary rock that captures much of the complex behavior observed in experiments. Like real sandstone, the virtual material was made of particles of a wide range of sizes stuck together in a 3D network. The results suggest that there may be microscopic changes in the material some time before a catastrophic break develops, even while experimental measurements show no obvious signs of trouble.
Many rocks are conglomerates of tiny grains cemented together, with small gaps or pores between them. The grains may have a wide range of sizes, with differing degrees of adhesion, so the mechanical properties are hard to describe in theoretical models that are simple enough to investigate, yet realistic enough to relate to the real world. For example, models based on networks of springs or rigid beams are too simplistic and idealized to compare with experiments.
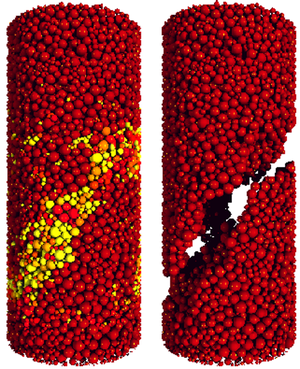
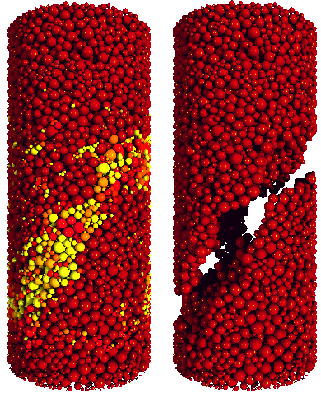
To overcome some of these limitations, Ferenc Kun of the University of Debrecen in Hungary and his co-workers built up a virtual porous solid in much the same way that real sedimentary rocks are formed: by allowing microscopic spheres of different sizes to settle into a layer and become stuck to one another, as they describe in Physical Review Letters. In this sticking process, the particles became connected by a network of “beams,” mimicking the cemented matrix that forms between grains in materials like sandstone. Unlike the material in many previous models, Kun says, “ours is three-dimensional and based directly on the microstructure observed in real sandstone.”
The researchers then simulated breaking their model rock, containing about 20,000 particles, by slowly moving the top layer of particles downward, compressing the layers below toward the breaking point. During the compression they found that cracks spread through the material in cascading avalanches of beam ruptures. Before the whole column of cemented particles broke apart catastrophically, there were a total of over 2000 “bursts” at erratic intervals, separated by quiescent periods when no beams broke.
The researchers compared their simulation results with indirect measurements of microcracking deduced from acoustic signals—sounds produced by microcracks in a material under stress. In a previous study, Kun and coworkers interpreted such observations with a simpler model in which “chains” of touching grains were approximated as continuous fibers [1].
With the new, more realistic model, Kun and colleagues have made a more detailed comparison with the acoustic data, as they describe in Physical Review Letters and in more detail in Physical Review E. Like the simulated cracking, the acoustic data consist of a series of short bursts. The researchers can plot the size of a burst vs. the probability of a burst of that size, producing a curve that slopes down to the right, since the largest bursts are the rarest. On logarithmic axes, this plot produced a straight line, indicating that the burst size and probability are related by a so-called power law: the probability depends on size raised to some exponent. The researchers found that their simulations agreed with the acoustic data for both the average value of the exponent and for the way in which the exponent decreases as catastrophic failure approaches.
“This is the first model to my knowledge that looks realistic and has a microstructure that evolves in a way that resembles actual experiments,” says Mikko Alava of Aalto University in Finland. “As a result, the [simulated] crackling noise of fracture has many features that more simple models do not have.” He adds that the model’s ability to reveal “the evolution of the internal force-carrying network is an important step forward.”
A material close to breaking apart exhibits some changes in its mechanical properties, such as a deviation from the usual rule that a solid deforms in direct proportion to the force applied to it. But the team says that the run-up to breakage can begin sooner than this—according to their model, damage can build up in the material before such macroscopic measures indicate anything unusual. “Our simulations reveal microscopic details of the failure process not readily accessible by experimental means,” says Kun.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- R. C. Hidalgo, C. U. Grosse, F. Kun, H. W. Reinhardt, and H. J. Herrmann, “Evolution of Percolating Force Chains in Compressed Granular Media,” Phys. Rev. Lett. 89, 205501 (2002)