Quantum Superrotor

Kenji Ohmori

Viewpoint

Quantum Superrotor

Kenji Ohmori

Institute for Molecular Science, National Institutes of Natural Sciences, Myodaiji, Okazaki 444-8585, Japan

March 19, 2014• Physics 7, 29

Molecules that rotate at very high rates exhibit surprising quantum coherence properties.

Figure caption — **Figure 1:** (Top) Optical centrifuge pulse (red) for making molecules rotate to form superrotors. Its linear polarization rotates, pulling the molecule with it. The unidirectional molecular rotation thus created is observed directly by coherent Raman scattering induced by the probe pulse (blue). (Bottom) Milner and colleagues have found that superrotors have interesting quantum coherence properties. Imagine the molecule as a dancer—slow rotation allows decoherence (the green dancer in the left; a fuzzy image) while fast rotation maintains coherence (the green dancer in the right; sharper image) against environmental influences (other dancers).

The rotational motion of an isolated molecule is among the simplest manifestations of angular momentum. More generally, angular momentum governs many important physical phenomena such as nuclear collisions, chemical reactions of atoms and molecules, and the emergence of superconductivity and magnetism in condensed matter. Molecular rotation can also be coupled easily to other internal degrees of freedom such as vibrational and electronic states. This efficient coupling offers opportunities for active control of quantum dynamics for fundamental studies and also for guiding chemical reactions toward desired outcomes.

As an example of this kind of control, a collaboration led by Valery Milner at the University of British Columbia, Canada, now reports in Physical Review Letters that they have used a laser pulse to turn diatomic molecules of oxygen and nitrogen into “superrotors”—molecules that rotate faster than $10^{13} hertz$ [1]. The energy of this superrotation is comparable to that of the chemical bond between the two atoms within the molecule and would require a temperature of $50, 000 kelvin$ to be realized in thermal equilibrium.

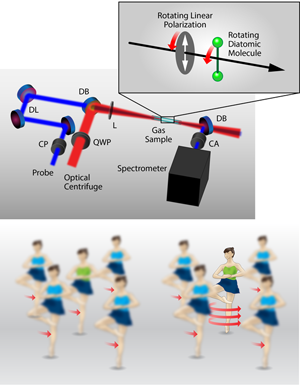
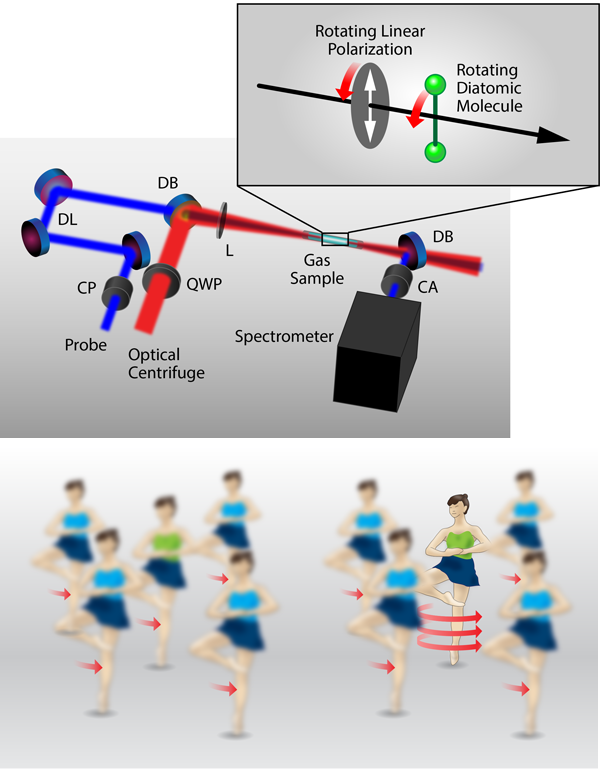
To drive these high rotational speeds, the UBC researchers used a sophisticated custom-tailored laser pulse whose duration is several tens of picoseconds. The polarization of this laser pulse is rotated unidirectionally and accelerated gradually within the pulse duration, forcing the molecule to follow (see Fig. 1). Milner and colleagues find that superrotors created in this way have a quantum coherence that is far more robust against collisions compared to the molecules in thermal equilibrium at room temperature.

This kind of optical manipulation of the amplitudes and phases of wave functions of matter is referred to as “coherent control” [2]. The concept was developed in the 1980s for controlling the dynamics of isolated molecules in the gas phase in processes such as ionization and dissociation induced by coherent laser light [3,4]. Since then it has attracted the attention of researchers studying a variety of physical systems, ranging from an isolated atom to many-body systems such as bulk solids and photosynthetic molecules.

One motivation arises from possible applications of coherent control in the development of novel quantum technologies such as quantum information processing and bond-selective chemistry. The latter is particularly attractive as a way of precisely breaking or forming specific chemical bonds of a molecule. Another important motivation is to better understand the wave nature of matter, and this knowledge is available only when we can control quantum systems actively. Coherent control of an isolated molecule in the gas phase has been one of the major targets, as it is the simplest system equipped with both electronic and nuclear degrees of freedom. In their work, Milner and colleagues have successfully controlled the rotational state of an isolated molecule in the gas phase.

Interest in spinning up a molecule into a superrotor was first raised by a research group in Canada [5]. They proposed a scheme in which a superrotor could be generated with a short laser pulse whose linear polarization axis rotates. This short laser pulse polarizes the molecule, so that its induced dipole follows the rotating laser polarization, a scheme called an “optical centrifuge.” The same group used an optical centrifuge to study a diatomic molecule, ${Cl}_{2}$ , experimentally, and they indirectly showed the generation of superrotors by observing the $Cl$ atoms that dissociate while in high rotational states [6]. However, there could be other possible sources of those fragments such as dissociation due to the electronic repulsion between two $Cl$ atoms within the molecule, even without any molecular rotation. It has therefore been necessary to verify the generation of a superrotor by its direct observation and to investigate its physical properties.

Researchers have made several advances in their ability to control the coherence of molecular rotation. Two independent groups, one in Israel and one in Japan, have created and observed unidirectional molecular rotation [7,8]. Milner and co-workers have demonstrated another approach to this unidirectional rotation of a molecule, as they report in their paper. Moreover, they have utilized this new approach to create and observe superrotors directly.

In their work, Milner and colleagues use the optical centrifuge to create the superrotation of $N_{2}$ and $O_{2}$ molecules. They create an ultrashort frequency-dispersed laser pulse, with its higher and lower frequency halves spatially separated. Independent phase modulation of the two spectral halves ensures that the frequencies of the two components increase and decrease linearly in $\sim 50$ picoseconds. These spectral components are circularly polarized in opposite directions, and when they are recombined they interfere with each other to create a linearly polarized pulse. When this is done, the polarization of this recombined laser pulse rotates unidirectionally with a difference frequency between the spectral components. As the difference frequency increases in time, the speed of the rotation becomes faster. The $N_{2}$ or $O_{2}$ molecule is irradiated with this recombined “centrifuge” laser pulse, so that its bond axis follows this unidirectional rotation of the laser polarization.

One important trick the authors use is to cut the high- and low-frequency tails of the spectral components, so that the amplitude of the laser field terminates suddenly at a certain point in time. The molecule follows the rotation of the laser polarization until this point and is released suddenly from the laser field to rotate freely like a boomerang. The other important trick is that they have employed a method known as coherent Raman scattering, which is induced by another short laser pulse to probe the molecular rotation. This allows the authors to directly observe, in real time, quantum coherence among multiple rotational eigenstates superposed coherently by the centrifuge pulse, in other words, a rotational wave packet. In addition, the Raman probe reveals the direction of the molecular rotation.

This ultrafast Raman probe was essential in allowing the authors to track the temporal evolution of the quantum coherence of the rotational wave packets during and after the centrifuge pulse. Remarkably, the quantum coherence lasts longer for the rotational quantum number $N = 50$ than for $N = 20$ by a factor of about $5$ , surviving as long as $1$ nanosecond at room temperature and atmospheric pressure. Milner and co-workers have thus verified that the quantum coherence of a superrotor is stable against collisions.

Studying why the coherence of the superrotor is more robust than that of a slow rotor may provide guidelines for the development of methods to decouple a quantum system from its environment. One possible reason for the quantum robustness of the superrotor may be its larger level spacing than that of a slow rotor; if so, researchers should be able to find a correlation between level spacing and coherence time.

The superrotor may also be useful for investigating many-body interactions. Theorists have predicted that the angular momenta of unidirectional molecular rotations could be converted to the angular momentum of a macroscopic vortex gas flow of an ensemble of those molecules [9]. The ultrahigh and unidirectional angular momenta of superrotors could allow us to see these vortices clearly. Coherent control started in isolated systems almost $30$ years ago, and is now moving on to many-body interacting systems [10]. The superrotor could offer many opportunities for us to look into those fundamental physics more deeply.

References

Aleksey Korobenko, Alexander A. Milner, and Valery Milner, “Direct Observation, Study, and Control of Molecular Superrotors,” Phys. Rev. Lett. 112, 113004 (2014)
K. Ohmori, “Wave-Packet and Coherent Control Dynamics,” Annu. Rev. Phys. Chem. 60, 487 (2009)
M. Shapiro, J. W. Hepburn, and P. Brumer, “Simplified Laser Control of Unimolecular Reactions: Simultaneous ( $ω_{1}, ω_{3}$ ) Excitation,” Chem. Phys. Lett. 149, 451 (1988)
D. J. Tannor, R. Kosloff, and S. A. Rice, “Coherent Pulse Sequence Induced Control of Selectivity of Reactions: Exact Quantum Mechanical Calculations,” J. Chem. Phys. 85, 5805 (1986)
J. Karczmarek, J. Wright, P. Corkum, and M. Ivanov, “Optical Centrifuge for Molecules,” Phys. Rev. Lett. 82, 3420 (1999)
D. M. Villeneuve, S. A. Aseyev, P. Dietrich, M. Spanner, M. Y. Ivanov, and P. B. Corkum, “Forced Molecular Rotation in an Optical Centrifuge,” Phys. Rev. Lett. 85, 542 (2000)
K. Kitano, H. Hasegawa, and Y. Ohshima, “Ultrafast Angular Momentum Orientation by Linearly Polarized Laser Fields,” Phys. Rev. Lett. 103, 223002 (2009)
O. Korech, U. Steinitz, R. J. Gordon, I. S. Averbukh, and Y. Prior, “Observing Molecular Spinning via the Rotational Doppler Effect,” Nature Photon. 7, 711 (2013)
U. Steinitz, Y. Prior, and I. S. Averbukh, “Laser-Induced Gas Vortices,” Phys. Rev. Lett. 109, 033001 (2012)
H. Katsuki et al., “All-Optical Control and Visualization of Ultrafast Two-Dimensional Atomic Motions in a Single Crystal of Bismuth,” Nature Commun. 4, 2801 (2013)

About the Author

Kenji Ohmori is a Professor at the Institute for Molecular Science (IMS) of the National Institutes of Natural Sciences in Okazaki, Japan, where he is also the Chairman of the Department of Photo-Molecular Science. After receiving his Ph.D. from The University of Tokyo in 1992, he was a Research Associate and an Associate Professor at Tohoku University. In 2003 he was appointed a Full Professor at IMS. His research interests focus on exploring the quantum-classical boundary and developing quantum technology based on the wave nature of matter. He is currently leading a JST-CREST project in which he combines an ensemble of ultracold Rydberg atoms and ultrafast coherent control to look into the dynamics in the transition from a delocalized wave function to a localized particle. He has been honored with the Japan Academy Medal (2007), JSPS Prize (2007), is a Fellow of the American Physical Society (2009), and has received the Humboldt Research Award (2012).