A Macroscopic Tractor Beam with Acoustic Waves
Among the many examples of how science fiction and fantasy have inspired real science, an interesting one is the “tractor beam,” first conceived by the chemical engineer and writer Edward E. Smith in the 1930s in his novel Spacehounds of IPC. Smith’s hypothetical device was a beam capable of pulling any macroscopic object from a distance. In the case of a light beam, however, this is counterintuitive, because we have known since Maxwell developed his electromagnetic theory that, owing to linear momentum, light exerts radiation pressure on matter in the direction of propagation. But at the microscopic level, an optical tractor beam has indeed been demonstrated: researchers have developed special optical beams that can pull nanoparticles opposite to the propagation direction [1]. Now, a step towards a device that works on macroscopic objects has been demonstrated by a group of researchers led by Michael MacDonald of the University of Dundee, Scotland, and Gabriel Spalding of Illinois Wesleyan University in Bloomington. They were able to scale the tractor beam up to handle centimeter-size objects, about 6 orders of magnitude larger than those manipulated by previous schemes, as reported in Physical Review Letters [2].
Optical versions of the tractor beam have their origin in the work of Arthur Ashkin in the 1970s, who discovered that light not only pushes microscopic matter along the propagation direction, but it also pulls neutral transparent objects towards the highest intensity regions [3]. This latter component of the optical force, identified by Ashkin as a “negative radiation pressure,” originates from the presence of strong intensity gradients. It is a conservative contribution, since it is derived from an energy potential, which acts as a restoring force capable of trapping objects in a localized region. This is the basis of optical tweezers and a myriad of micromanipulation techniques that have led to spectacular advances in the physical sciences and beyond. Nevertheless, the original concept of creating a negative radiation pressure with nonconservative forces (i.e., forces that change mechanical energy in the system when pushing or pulling a particle) is appealing. The reason is that such forces do not require tailored intensity gradients, which are difficult to produce with acoustic systems in comparison with optical systems. This in turn would add new flexibility to manipulation techniques, as well as providing fundamental information about matter-wave interactions.
Researchers in acoustics made the first theoretical advances in this direction. Partly inspired by developments in optical traps, they studied analogous acoustic systems and noticed that a nonconservative force opposite to the propagation direction could arise under certain circumstances [4,5]. These ideas led to the use of positive nonconservative acoustic forces to, for instance, transfer angular momentum and exert torques on macroscopic objects [6], as it was done previously with light [7]. The tractor beam idea was soon revisited in optics as well, first from a theoretical perspective [8–10], and then finally demonstrated with light beams acting on submicron-sized particles [1].
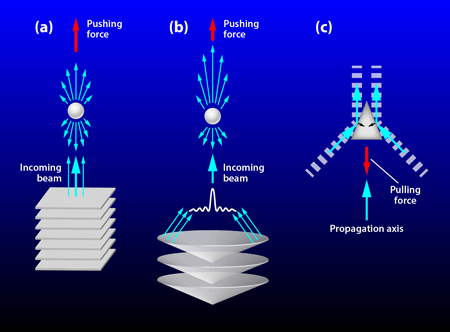
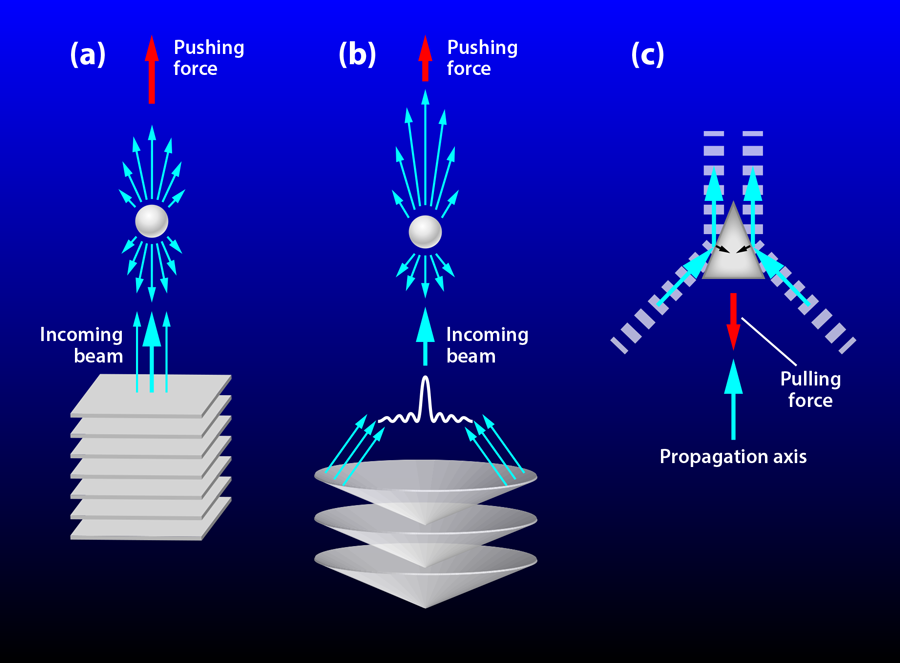
The work by MacDonald, Spalding, and co-workers now considerably extends the size of objects that can be manipulated with a tractor beam. This ability is due to some key concepts. Whereas the positive radiation pressure acting on an object is the result of the backscattered radiation, there are situations in which forward scattering can dominate; this is the heart of negative radiation pressure. Of course, the scattering direction is determined by the direction of the incident wave on an object. A plane wave, for instance, can never give rise to scattered waves whose propagation vectors have larger components along the original propagation axis than that of the incident wave [Fig. 1(a)]. Consider, in comparison, a wave field propagating along a main axis but constituted by a superposition of waves whose individual wave vectors subtend large angles with respect to the main propagation axis; this is known as a nonparaxial beam. A particular example is the Bessel beam, whose component wave vectors lie on the surface of a cone [4,5,9,10].
If a nonparaxial Bessel beam impinges on a target, part of the diffracted radiation may indeed have larger wave vector components along the propagation axis than those of the incident waves, giving rise to strong forward scattering. The net effect might be either a decreasing of the positive radiation pressure (pushing force) [(Fig. 1(b)] or even a negative radiation pressure (pulling force), depending on the shape of the object, its size, and its interaction with the wave field. Furthermore, if the object and the field are properly designed, the effect can be maximized, which is precisely what the authors did. In contrast with the optical domain, in which light’s linear momentum changes as a consequence of several processes such as reflection, refraction, and absorption, sound waves, because of the large differences in the sound speed commonly found between different media, are mainly reflected and absorbed. Therefore, the authors designed a scheme aimed at minimizing the forward force due to the absorbed radiation: they built two targets in the form of hollow isosceles triangular prisms [Fig. 1(c)] with different apex angles, whose sides had large acoustic reflectivity, and with an acoustic absorber on the base. In addition, the acoustic field impinging on the target was sculpted as a rectilinear analog of a nonparaxial Bessel beam, with only two wave-vector components.
In order to generate the tailored acoustic field, the team used a square matrix array of about 1000 transducers, operating at ultrasound frequency ( 550 kilohertz), placed at the bottom of a water-filled chamber. Each one can be individually addressed, not only with on-off states, but also by programming up to eight discrete phase values. This device allows the researchers to imprint a spatial modulation on the emitted acoustic field. In this case, the generated patterns behave, in the region of interest, as a pair of plane waves whose wave vectors are symmetrically inclined towards the array centerline, where the target was suspended from a force balance. The two waves intersect at a certain height over the array plane, having a hollow core underneath; the height of the intersection point can be readjusted by changing the emission pattern from the array.
By varying the vertical position of the target, the researchers were able to obtain a detailed map of the acoustic force as a function of the distance from the object to the source plane, which was measured in terms of changes in weight of the target. Based on a theoretical analysis, two contributions of the force were clearly identified; a negative (pulling) force due to the reflection in the walls of the prisms, and a positive (pushing) one, owed to the absorbed radiation at the base. The qualitative behavior of the total force and its order of magnitude (millinewtons) agreed well with the experiments. The equilibrium position, where the two contributions of the force are exactly balanced, can be controlled by reconfiguring the acoustic field. All the measurements were done for different configurations of the acoustic pattern and for each of the two targets, whose volumes are of the order of tens of cubic centimeters.
Although the intensity gradients may play a role in the force towards the low-pressure regions, the careful design of the experiment for maximizing the forward scattering, the ability to control the equilibrium position, and the fair comparison with simulations guarantee that the main role is indeed played by the scattering force. Therefore, this is the first demonstration of a nonconservative pulling force in the acoustics realm, which complements previous demonstrations in optics.
In addition, the authors point out the potential impact that the control of acoustic forces and the generation of structured ultrasound fields may have in modern biomedical techniques. In therapeutic treatments involving focused high-intensity fields, for example, the precise control of energy deposition could be greatly improved with the use of complex beams.
Interaction between matter and waves always seems to surprise scientists in new ways. The more we advance in the study and generation of structured wave fields and novel materials, the higher the possibility of finding new effects and applications.
References
- O. Brzobohaty, Karásek M. Siler, L. Chvátal, T. Cizmar, and P. Zemánek, ”Experimental Demonstration of Optical Transport, Sorting and Self-Arrangment Using a ‘Tractor Beam’,” Nature Photon. 7, 123 (2013)
- Christine E. M. Démoré, Patrick M. Dahl, Zhengyi Yang, Peter Glynne-Jones, Andreas Melzer, Sandy Cochran, Michael P. MacDonald, and Gabriel C. Spalding, “Acoustic Tractor Beam,” Phys. Rev. Lett. 112, 174302 (2014)
- A. Ashkin, “Acceleration and Trapping of Particles by Radiation Pressure,” Phys. Rev. Lett. 24, 156 (1970)
- P. L. Marston, “Axial Radiation Force of a Bessel Beam on a Sphere and Direction Reversal of the Force,” J. Acoust. Soc. Am. 120, 3518 (2006)
- F. G. Mitri, “Negative Axial Radiation Force on a Fluid and Elastic Spheres Illuminated by a High-Order Bessel Beam of Progressive Waves,” J. Phys. A 42, 245202 (2009)
- K. Volke-Sepúlveda, A. Santillán and R. Boullosa, “Transfer of Angular Momentum to Matter from Acoustical Vortices in Free Space,” Phys. Rev. Lett. 100, 024302 (2008)
- H. He, M. Friese, N. Heckenberg, and H. Rubinsztain-Dunlop, “Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity,” Phys. Rev. Lett. 75, 826 (1995)
- S. Sukhov and A. Dogariu, ”Negative Nonconservative Forces: Optical ‘Tractor Beams’ for Arbitrary Objects,” Phys. Rev. Lett. 107, 203602 (2011)
- J. Chen, J. Ng, Z. Lin, and C. T. Chan, “Optical Pulling Force,” Nature Photon. 5, 531 (2011)
- A. Novitsky, C.-W. Qiu, and H. Wang, “Single Gradientless Light Beam Drags Particles as Tractor Beams,” Phys. Rev. Lett. 107, 203601 (2011)