Hiking Trails in Attosecond Landscapes
Short-pulse lasers allow the most accurate measurement of fast phenomena such as the dynamics of atoms and even electrons. Unfortunately, pulses in the visible region of the spectrum cannot be shorter than the period of one optical cycle: a couple of femtoseconds (one femtosecond is a millionth of a billionth of a second). However, this limit can be overcome when the laser field is very strong, so that its interaction with matter becomes extremely nonlinear, enabling one to zoom in and initiate processes that evolve during a fraction of an optical cycle [1]. This breakthrough, known as high-harmonic generation or HHG, lets researchers produce electromagnetic pulses with durations of attoseconds (thousandths of a femtosecond) and wavelengths in the extreme-ultraviolet or x-ray regime. In Physical Review X, a collaboration lead by Andrius Baltuška of the Technical University of Vienna, Austria, demonstrates an important advance in HHG, showing that carefully chosen combinations of three synchronized optical beams can produce higher frequencies and photon flux [2]. Controlling the generation of these pulses is essential for the observation and manipulation of extremely fast phenomena, such as multielectron processes.
To what extent can we tailor attosecond pulses and what are the main knobs and control parameters for doing so? Addressing this question requires a careful look into their generation mechanism. Attosecond pulses are produced during the electron-ion collisions induced by a strong laser field, usually referred to as “re-collisions.” Within one optical period, an electron is removed from the atom, accelerated by the strong laser field, and re-collides with the parent ion. The re-collision process can lead to the emission of attosecond extreme-ultraviolet (XUV) pulses. The optical properties of the emitted pulses—their spectral bandwidth, temporal shape, and strength—are determined by the electric field of the laser. However, the time variation of this laser field is usually dictated by the basic sinusoidal oscillation of a single cycle.
The generation of the attosecond pulses can be viewed as an extremely accurate time-resolved measurement of electronic dynamics. In this picture, tunnel ionization serves as the “pump,” launching the electron’s motion, while the recollision serves as a “probe,” effectively mapping the evolved wave function onto the emitted radiation. Although this picture has been applied successfully to small molecular systems, its extension to more complex systems poses a significant challenge. The dynamics can evolve through numerous routes, for example, multiple ionization channels, that are strongly coupled by the fundamental laser field. As long as one is constrained by the sinusoidal shape of the optical cycle, the rich, multidimensional information that describes the dynamics remains elusive.
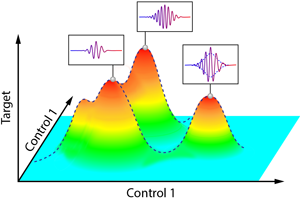
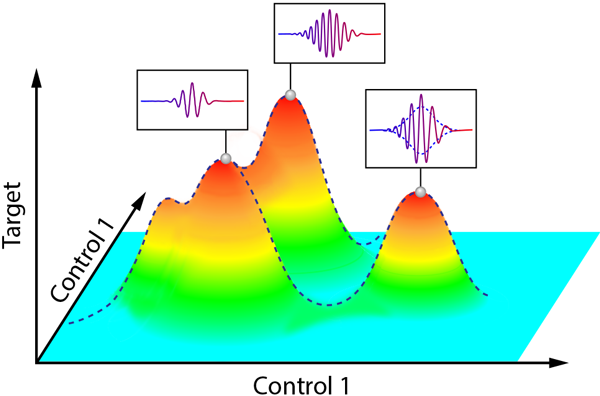
Recent pioneering studies have overcome this limitation by shaping the temporal profile of the laser pulse within the optical cycle [3,4]. Sculpturing the electric field on an attosecond time scale opens the door for novel control schemes that aim to manipulate the electronic degrees of freedom. One powerful example is demonstrated by Baltuška and co-workers: the shaping of the driving optical cycle in order to control the properties of the resulting attosecond pulses. They address the following question: “What subcycle shape provides the highest maximum (cutoff) frequency or photon flux?” Answering this question requires a search in a multidimensional landscape, shaped by the subcycle nature of the interaction itself (see Fig. 1).
Historically, similar questions were asked regarding the “coherent control” of molecular or solid-state systems on much longer time scales (femtoseconds or picoseconds) [5]. One successful example is the tailoring of the temporal shape of femtosecond optical pulses. This was done, in the visible or infrared regime, by manipulating the phase across the pulse’s spectrum. As long as the interacting field is relatively weak, it was demonstrated that the shape of the optical pulse can dictate the quantum state of small molecular systems by selecting their vibrational modes, ionization probability, or dissociation paths. However, the extension of these schemes to attosecond pulses is very challenging because of their high frequency and their very broad spectrum, tens or hundreds of times larger in width than optical pulses.
The authors apply a completely different approach, manipulating the attosecond pulses during the generation process itself. Previously, a similar approach was demonstrated in a limited form, combining two colors or manipulating the absolute carrier envelope phase to shape the spectrum of a single attosecond pulse [6], reduce its spectral bandwidth [7,8], or enhance its total intensity [9,10]. Following the pioneering work [3,4], the authors [2] go a step further: they demonstrate subcycle shaping of the generating light based on the synthesis of three discrete spectral bands covering 1.6 octaves (a factor of 3 in frequency). The independent manipulation of the three spectral bands gives them multidimensional control of the electron’s time of birth, time of return, and the intervening trajectory in the continuum. Following a theoretical proposal [11], they search for the “perfect waveform” that will optimize the cutoff frequency. The authors approximate such an ideal waveform by combining three colors generated with precise relative phase from a single source. The result is an extension of the measured cutoff frequency and an enhancement by 2 orders of magnitude of the photon flux. Furthermore, multidimensional control over the basic parameters of recollision allows an accurate manipulation of the spectral shape of the attosecond pulses.
Attosecond pulse shaping is in its pioneering stage, opening many new exciting pathways to manipulate quantum processes with attosecond resolution. While Baltuška and his colleagues demonstrated an important step along this route, we can already look forward to future advances. Rapid progress in laser technology should allow this scheme to be extended to more frequency bands, thus increasing the number of “knobs” available for control. In parallel, progress in attosecond sources offers the exciting possibility of seeding this control mechanism with external attosecond pulses, increasing the temporal resolution by which the subcycle recollision process is shaped. Can subcycle pulse shaping be used to manipulate electronic wave functions, similar to what has been done for molecular wave functions through femtosecond pulses? Can we tailor multielectron phenomena such as Auger decay or select specific reaction pathways to implement charge-directed reactivity? These open questions define some of the most important challenges in attosecond science.
References
- P. B. Corkum and F. Krausz, “Attosecond Science,” Nature Phys. 3, 381 (2007)
- S. Haessler et al., “Optimization of Quantum Trajectories Driven by Strong-Field Waveforms,” Phys. Rev. X 4, 021028 (2014)
- A. Wirth et al., “Synthesized Light Transients,” Science 334, 195 (2011)
- S.-W. Huang et al., “High-Energy Pulse Synthesis with Sub-Cycle Waveform Control For Strong-Field Physics,” Nature Photon. 5, 475 (2011)
- M. Shapiro and P. Brumer, Quantum Control of Molecular Processes (Wiley-VCH, Weinheim, 2012), 2nd ed[Amazon][WorldCat]
- F. Krausz and M. Ivanov, “Attosecond Physics,” Rev. Mod. Phys. 81, 163 (2009)
- O. Raz, O. Pedatzur, B. D. Bruner, and N. Dudovich, “Spectral Caustics in Attosecond Science,” Nature Photon. 6, 170 (2012)
- R. Bartels, S. Backus, E. Zeek, L. Misoguti, G. Vdovin, I. P. Christov, M. M. Murnane, and H. C. Kapteyn, “Shaped-Pulse Optimization of Coherent Emission of High-Harmonic Soft X-Rays,” Nature 406, 164 (2000)
- I. Jong Kim et al., “Highly Efficient High-Harmonic Generation in an Orthogonally Polarized Two-Color Laser Field,” Phys. Rev. Lett. 94, 243901 (2005)
- F. Brizuela et al., “Efficient High-Order Harmonic Generation Boosted By Below-Threshold Harmonics,” Sci. Rep. 3, 1410 (2013)
- L. E. Chipperfield, J. S. Robinson, J. W. G. Tisch, and J. P. Marangos, “Ideal Waveform to Generate the Maximum Possible Electron Recollision Energy for any Given Oscillation Period,” Phys. Rev. Lett. 102, 063003 (2009)