Scalable Imaging of Superresolution

Jonathan C.F. Matthews

Viewpoint

Scalable Imaging of Superresolution

Centre for Quantum Photonics, H. H. Wills Physics Laboratory, Tyndall Avenue, Bristol BS8 1TL, United Kingdom

June 2, 2014• Physics 7, 59

Researchers have demonstrated a viable approach to efficiently observing superresolved spatial interference fringes that could improve the precision of imaging and lithography systems.

Figure caption — **Figure 1:** (a) Superresolution and supersensitivity. Examples of interference fringes of (i) a single-photon interference fringe (dot-dash line, $sin ϕ$ ), (ii) interference fringe at twice the resolution from a two-photon NOON state (solid line, $sin 2 ϕ$ ), and (iii) interference fringe obtained from classical light at twice the resolution, with reduced visibility (dashed line, $\frac{1}{2} sin 2 ϕ$ ). Example schematics of two-photon and classical-light interferometers. (b) Illustration of an $n$ -photon Fock state in a diffraction limited beam falling on an array of detectors smaller than the beam. The optical centroid measurement uses postprocessing to harness all of the photon detection events to scalably detect the Fock state. Without this—even with photon-number-resolving single-photon detectors that are smaller than a diffraction limited spot—one cannot efficiently detect the Fock state $| n 〉$ .

Early on, a physics student learns that interference fringes in optics form the basis for constructing sensitive measurement apparatus, for imaging systems, and lithography processes. According to classical optics, the period of oscillation of interference fringes of light with wavelength $λ$ are bound by the classical model of light to the diffraction limit $\sim λ / 2$ . Fourteen years ago, researchers proposed a form of imaging that uses entangled quantum states of light to produce spatial interference patterns with better resolution than what is possible with a classical model of optics [1]. The goal is to use supersensitive interference patterns to provide more information about a measured quantity such as distance, mechanical deviation, or refractive index, and in the case of spatial interference, defeat the diffraction limit.

While a range of subdiffraction imaging techniques exist, such as near-field scanning optical microscopy, there is tremendous interest in the prospect of alternative methods to spatially resolve optical interference patterns below the diffraction limit, using conventional focusing techniques. Critically, the proposal of using entangled states of light enables just this, with, in principle, a linear increase in the frequency of the resulting interference with the number of photons comprising each quantum state. Without considering state generation or detection techniques, this would appear to yield a scalable (i.e., an efficient) increase in resolution—this is an exciting prospect. However, until recently, this line of research had been stalled by the rather major problem of how to efficiently observe such interference patterns. In a paper in Physical Review Letters, Rozema and colleagues [2] report an advance in quantum imaging by showing it is possible to efficiently observe the increasingly superresolved interference patterns produced by entangled states. They test the approach using a series of entangled states known as NOON states.

Many proposals for quantum-enhanced metrology and for quantum-enhanced imaging rely on NOON states. In general, these states are multiparticle states of $N$ indistinguishable particles (in optics, photons), in a quantum superposition in which the photons are localized in each of two separate optical modes $a$ , $b$ (such as path or polarization). This is denoted as $(| N 〉_{a} | 0 〉_{b}) + (| 0 〉_{a} | N 〉_{b}) / \sqrt{2}$ .

Their main beneficial feature is that when they pass through a process (such as inside an interferometer) that causes a relative phase shift of $ϕ$ between the two modes, they pick up an $N$ -fold phase shift. This in turn means that recombination of the two optical modes reveals an interference fringe that oscillates $N$ times faster than could be achieved with classical light, such as a laser of the same wavelength. This superresolved interference was first reported as the modulation of coincidental photon detection rate in an interferometer, in 1990 for $N = 2$ photons [3,4]. Since then, researchers have increased $N$ to $5$ photons [5], where in each $N > 2$ case, postselection methods are employed to observe the behavior of NOON states (in the absence of generating NOON states exactly, without unwanted photons occupying the same modes). Proof-of-principle demonstrations are emerging to show how NOON states can possibly be used for biosensing [6] and entanglement-enhanced microscopy [7,8].

The choice of how to generate NOON states by the authors may likely prove to be the workhorse for imaging with NOON states of increasing size over the next few years. Cable and Dowling [9] calculated that they can be generated exactly if one uses a scalable number of resources, but this is very similar to those required for linear optical quantum computing. Another approach that generates approximate NOON states with high fidelity appears simpler, using the quantum interference of a laser beam and a $2$ -mode squeezed state (that is the state that is generated from spontaneous parametric down-conversion) when carefully overlapped at a beam splitter [10]. This is the method Rozema and colleagues [2] employ to generate $2$ -, $3$ -, and $4$ -photon superresolved interference patterns and is proving to be a promising approach for readily accessing high-photon-number supersensitive fringes (used also in preceding Refs. [5,8]).

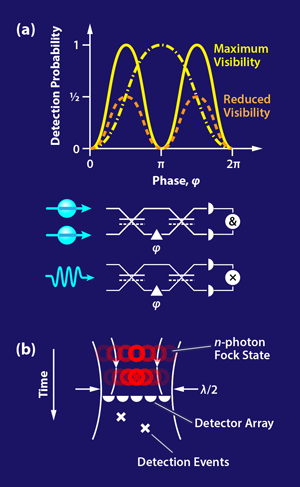
Superresolution can also be achieved using classical light [11] [see Fig. 1(a)], but this comes at the cost of rapidly degraded interference patterns. This reduces their practical utility, in particular in potentially noisy low-photon-flux scenarios. Rozema and colleagues [2] explore this in the context of their spatial interference scenario and show that the visibility of classically superresolved fringes degrades exponentially, while the visibility of the entangled light fringes remains constant with increasing photon number for $N = 2, 3, 4$ , demonstrating a clear quantum advantage. This is an important step in demonstrating scalability and indicates that as $N$ increases further, even more advantage can be gained.

However, an obstacle to use NOON states with large $N$ is that their resulting spatial interference patterns become exponentially difficult detect, and so all of the effort of generating NOON states for imaging might have seemed rather pointless—proposals of how to image spatially super resolved interference from NOON states rely on detecting $n$ -photon states called Fock states ( $| n 〉$ ), which until recently appeared to perform exponentially badly with increasing $n$ . Thanks to a proposal of Tsang [12] (see 22 June 2009 Viewpoint) and the first proof-of-principle experiment from the Boyd group for $N = 2$ [13], Rozema and colleagues [2] have demonstrated the converse; it is possible and practical to detect and image the superresolved interference patterns of increasing NOON states.

Essentially, the problem of detecting large $N$ NOON state spatial interference patterns comes down to the fact that while $n$ photons might be localized in an optical mode, this mode is spatially diffraction limited and so cannot be focused to spot sizes smaller than $\sim λ / 2$ [see Fig. 1(b)]. For detectors of size $r < λ / 2$ that are smaller than the spot size of the mode, photons in the Fock state appear to the detectors in superposition spatially across this mode—detecting each photon collapses this wave function and so the photon can only appear at one detector, with probability defined by the mode profile, but we can approximate as $2 r / λ$ . Therefore the probability to detect the state $| n 〉$ at one detector is equivalent to $(2 r / λ)^{n}$ —a likelihood that very quickly drops (exponentially with $n$ ) to zero. Relying on this clearly negates the benefits of using NOON states of increasing size to obtain high-visibility superresolution. The proposal of Tsang [12] applied by Rozema and colleagues [2] to observe $N = 2, 3, 4$ NOON states was to combine the detection events registered by all detectors in an array and perform some postprocessing to compute the centroid of the detection events. This is sufficient to reveal the superresolved interference and, importantly, scales favorably for practical applications.

Despite the achievement of Rozema et al., the job is by no means done. Namely, this scheme is affected by the collection and detection efficiency of single-photon detectors. The probability of $n$ photons detected by separate detectors scales like $p^{n}$ , where $p$ is now the quantum efficiency of each detector—this highlights the need for highly efficient single-photon detectors. Thankfully, several detector options are emerging in the form of transition edge sensors [14] and superconducting nanowire single-photon detectors [15]. While this demonstration does indicate great promise for the performance of NOON states with increasing photon number, the behavior of NOON states of more than five entangled photons is yet to be demonstrated, requiring brighter photon sources than available now. And NOON states themselves are particularly susceptible to degradation in performance in the presence of loss [16]—this is being addressed with loss-tolerant approaches to quantum metrology. But while there are indeed many challenges ahead, efficient detection of increasingly superresolved spatial interference fringes certainly provides the imaging community with new and exciting quantum-enhanced techniques.

References

A. N. Boto, P. Kok, D. S. Abrams, S. L. Braunstein, C. P. Williams, and J. P. Dowling, “Quantum Interferometric Optical Lithography: Exploiting Entanglement to Beat the Diffraction Limit,” Phys. Rev. Lett. 85, 2733 (2000)
Lee A. Rozema, James D. Bateman, Dylan H. Mahler, Ryo Okamoto, Amir Feizpour, Alex Hayat, and Aephraim M. Steinberg, “Scalable Spatial Superresolution Using Entangled Photons,” Phys. Rev. Lett. 112, 223602 (2014)
Z. Y. Ou, X. Y. Zou, L. J. Wang, and L. Mandel, “Experiment on Nonclassical Fourth-Order Interference,” Phys. Rev. A 42, 2957 (1990)
J. G. Rarity, P. R. Tapster, E. Jakeman, T. Larchuk, R. A. Campos, M. C. Teich, and B. E. A. Saleh, “Two-Photon Interference in a Mach-Zehnder Interferometer,” Phys. Rev. Lett. 65, 1348 (1990)
I. Afek, O. Ambar, and Y. Silberberg, “High-NOON States by Mixing Quantum and Classical Light,” Science 328, 879 (2010)
A. Crespi, M. Lobino, J. C. F. Matthews, C. R. Neal, R. Ramponi, R. Osellame, and J. L. O’Brien, “Measuring Protein Concentration with Entangled Photons,” Appl. Phys. Lett. 100, 233704 (2012)
T. Ono, R. Okamoto, and S. Takeuchi, Nature Commun. 4, 2426 (2013)
Y. Israel, S. Rosen, and Y. Silberberg, “Supersensitive Polarization Microscopy Using NOON States of Light,” Phys. Rev. Lett. 112, 103604 (2014)
H. Cable and J. P. Dowling, “Efficient Generation of Large Number-Path Entanglement Using Only Linear Optics and Feed-Forward,” Phys. Rev. Lett. 99, 163604 (2007)
H. F. Hofmann and T. Ono, “High-Photon-Number Path Entanglement in the Interference of Spontaneously Down-Converted Photon Pairs with Coherent Laser Light,” Phys. Rev. A 76, 031806 (2007)
K. J. Resch, K. L. Pregnell, R. Prevedel, A. Gilchrist, G. J. Pryde, J. L. O’Brien, and A. G. White, “Time-Reversal and Super-Resolving Phase Measurements,” Phys. Rev. Lett. 98, 223601 (2007)
M. Tsang, ”Quantum Imaging beyond the Diffraction Limit by Optical Centroid Measurements,” Phys. Rev. Lett. 102, 253601 (2009)
H. Shin, K. W. Chan, H. J. Chang, and R. W. Boyd, “Quantum Spatial Superresolution by Optical Centroid Measurements,” Phys. Rev. Lett. 107, 083603 ((2011))
A. E. Lita, A. Miller, and S. W. Nam, Opt. Express 16, “Counting Near-Infrared Single-Photons with $95 %$ Efficiency,” 3032 (2008)
W.H.P. Pernice, C. Schuck, O. Minaeva, M. Li, G.N. Goltsman, A.V. Sergienko, and H.X. Tang, “High-Speed and High-Efficiency Travelling Wave Single-Photon Detectors Embedded in Nanophotonic Circuits,” Nature Commun. 3, 1325 (2012)
J. P. Dowling, ”The Lowdown on High-N00N States,” Contemp. Phys. 49, 125 (2008)

About the Author

Jonathan Matthews is a Leverhulme Trust Early Career Research Fellow at the Centre for Quantum Photonics, University of Bristol, UK. Originally a mathematics graduate, he received his physics Ph.D. in 2011 at the University of Bristol, for implementing integrated quantum photonic circuitry for multiphoton demonstrations of quantum technology. His research interests include quantum metrology, analog quantum simulations, and quantum computing componentry. He now leads the quantum metrology research at the Centre for Quantum Photonics.