Pure Photons for Quantum Communications

Monika Schleier-Smith; Haruka Tanji-Suzuki

Viewpoint

Pure Photons for Quantum Communications

Monika Schleier-Smith

Department of Physics, Stanford University, Stanford, CA 94305, USA

Haruka Tanji-Suzuki

Photon Science Center, The University of Tokyo, Tokyo 113-8656, Japan

January 21, 2014• Physics 7, 6

Researchers characterize a single-photon source, proving it emits nonclassical states of light that may be useful for quantum communication schemes.

Figure caption — **Figure 1:** (Top) Experimental setup for single-photon generation and tomographic characterization. A “write” laser pulse stores an excitation in a quantum memory made of a cloud of cold rubidium atoms. A “read” pulse converts this excitation into an emitted single photon that is characterized by interferometric measurements. (Bottom) Tomographic reconstruction reveals that the Wigner function of the single photon dips to negative values (blue), proving that the quantum state of light is nonclassical.

The visionaries of quantum information foresee an era where illicit eavesdropping on fiber-optic communications will be prohibited by the fundamental laws of quantum mechanics. If each qubit of information is conveyed by a single, indivisible photon, then it cannot be intercepted without attracting the notice of the intended recipient. Yet in practice, photons do not ordinarily travel alone: a laser pulse containing on average one photon sometimes contains two and often contains none. Hence considerable effort has been directed towards developing devices capable of producing precisely one photon at the push of a button. Typically, the performance of single-photon sources is benchmarked by the suppression of two-photon events. But a more complete characterization of the emitted light field is necessary to assess the potential of such sources for long-distance quantum communications. A new experiment by Erwan Bimbard and colleagues at the Institute of Optics of the Paris-Sud University, reported in Physical Review Letters [1], shows that a cloud of cold rubidium atoms can be triggered to efficiently emit single photons of unprecedented purity, as certified by a stringent test of nonclassicality.

Tests of nonclassicality are vital to the development of quantum technologies. Perhaps the most famous are those used to prove entanglement between qubits (e.g., violations of Bell’s inequalities). Bimbard et al. subject their device to a test inspired by a different paradigm for encoding quantum information, wherein discrete qubits are supplanted by continuous variables: the two quadrature components $x$ and $p$ of the light’s oscillating electric field $E = x cos ω t + p sin ω t$ . Just like the position and momentum of a particle, $x$ and $p$ are noncommuting observables that cannot be determined simultaneously to arbitrary precision. Consequently, it is not always possible to write down a joint probability distribution $P (x, p)$ for measurements of $x$ and $p$ . The closest analog allowed by quantum mechanics is the so-called “Wigner function” $W (x, p)$ , defined so that integrating over all possible values of $p$ yields the probability distribution for measurement outcomes of $x$ and vice versa. This Wigner “quasiprobability,” unlike a true probability distribution, can take on negative values—a striking signature of nonclassicality. Bimbard et al. show that the output of their single-photon source exhibits negativity of the Wigner function and therefore defies description by any classical model.

Why subject a single-photon source—a device designed for transmitting discrete qubits over quantum networks—to a test designed for continuous variables? One reason is that the technical requirements for mapping out the Wigner function are closely aligned with those for long-distance quantum communication. The Wigner function is a complete description of the quantum state of a single mode of the electromagnetic field, with a designated spatial profile, frequency, and polarization. Any chance of loss from the designated mode—or, equivalently, any unpredictability in the characteristics of the light field—contaminates the single-photon state with a contribution from the zero-photon state, whose Wigner function is everywhere positive. Observing Wigner negativity thus requires efficient channeling of a single photon into a predetermined field mode. This same requirement is also a key ingredient in the design of quantum repeaters [2]: two adjacent nodes in a quantum network can be entangled if induced to emit photons that can be coupled into a common mode of light.

To deliver photons into a well-defined field mode, the authors adopt a scheme from a landmark proposal [2] for building quantum repeaters out of atomic ensembles. A sufficiently long, optically dense cloud of atoms can scatter light in a highly directional manner if the fields scattered by all atoms interfere constructively along the extent of the cloud. Bimbard et al. exploit this phenomenon, using a cloud of ten thousand rubidium atoms, laser-cooled to achieve a high density and to minimize Doppler broadening. Following the example of Ref. [3], they position the atoms between two mirrors forming an optical resonator, so that any light emitted by the ensemble recirculates through it $\sim 100$ times, enhancing the length of interaction and the directionality of emission. Beyond serving as a directional light source, the atomic ensemble constitutes a quantum memory, capable of storing information in the atoms’ internal states. Such stored information can then be transmitted over a quantum network by controllably converting atomic excitations into emitted photons.

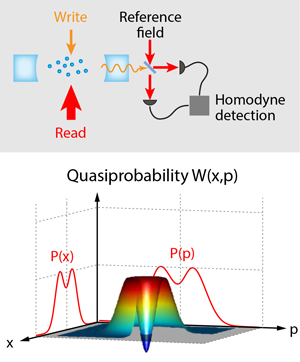
To prepare for the generation of a single photon, the researchers first write into the quantum memory a single excitation, shared collectively among all atoms in a quantum superposition state (see Fig.1). They do this by driving the atoms with a series of very weak laser pulses, so that one out of every thousand tries (on average) produces a change in the internal state of one atom. In the process, one photon is scattered into the cavity mode, and detecting this photon heralds the successful initialization of the quantum memory. A second, much stronger laser pulse triggers the conversion of the atomic excitation into a single “read” photon. The read photon, in contrast to the heralding photon, is generated deterministically, at a time set by the trigger pulse.

To reconstruct the Wigner function of the read photon, Bimbard et al. employ a method akin to medical tomography. Just as one may reconstruct a full three-dimensional model of the brain from images integrated along various lines of sight, so can one obtain the Wigner quasiprobability distribution from a set of its line-of-sight integrals [4]. The latter are ordinary probability distributions for measurements of components of the light field, e.g., $\int W (x, p) d p = P (x)$ . Such measurements can be performed by combining the light of interest (the read photon) with a much stronger reference beam and detecting the interference between the two fields. Varying the phase of the reference beam is then equivalent to varying the imaging axis in the brain scanner. Yet whereas a brain scan will never indicate a negative tissue density, the reconstructed Wigner function indeed reaches negative values (see Fig.1). The diagnosis is clear: the read field violates the laws of classical physics.

Bimbard et al.’s is not the first measurement of the single-photon Wigner function [5,6]. What is new is the high-fidelity transfer of a nonclassical state from an atomic quantum memory onto a light field, sufficient to preserve the Wigner negativity. On the one hand, this represents a milestone in the efficiency and purity of single-photon generation, vital for linking storage nodes in quantum networks by flying optical qubits. Yet an even greater impact may be in advancing the competing paradigm of encoding quantum information in continuous variables. Here, Wigner negativity is a computational resource [7] that could enable operations such as error correction [8] and entanglement distillation [9], essential to combating the noise and losses inevitable in telecommunications.

An important next step will be to improve the duty cycle of the atom-light interface. In the current experiment, it takes more than ten milliseconds to prepare an excitation that lives for less than a microsecond. Technical improvements—such as confining the atoms in an optical lattice to minimize motional decoherence [10]—will be required to increase the duty factor. Applications would also benefit from an ability to generate a greater diversity of quantum states, including superpositions of higher photon numbers. The key to doing so may lie in engineering interactions between the atoms to extend their role beyond that of a passive storage medium to that of a versatile quantum information processor.

References

Erwan Bimbard, Rajiv Boddeda, Nicolas Vitrant, Andrey Grankin, Valentina Parigi, Jovica Stanojevic, Alexei Ourjoumtsev, and Philippe Grangier, “Homodyne Tomography of a Single Photon Retrieved on Demand from a Cavity-Enhanced Cold Atom Memory,” Phys. Rev. Lett. 112, 033601 (2014)
L. M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, “Long-distance quantum communication with atomic ensembles and linear optics,” Nature 414, 413 (2001)
J. Simon, H. Tanji, J. K. Thompson, and V. Vuletić, “Interfacing Collective Atomic Excitations and Single Photons,” Phys. Rev. Lett. 98, 183601 (2007)
K. Vogel and H. Risken, “Determination of Quasiprobability Distributions in Terms of Probability Distributions for the Rotated Quadrature Phase,” Phys. Rev. A 40, 2847 (1989)
A. I. Lvovsky, H. Hansen, T. Aichele, O. Benson, J. Mlynek, and S. Schiller, “Quantum State Reconstruction of the Single-Photon Fock State,” Phys. Rev. Lett. 87, 050402 (2001)
J.-I. Yoshikawa, K. Makino, S. Kurata, P. van Loock, and A. Furusawa, “Creation, Storage, and On-Demand Release of Optical Quantum States with a Negative Wigner Function,” Phys. Rev. X 3, 041028 (2013)
A. Mari and J. Eisert, “Positive Wigner Functions Render Classical Simulation of Quantum Computation Efficient,” Phys. Rev. Lett. 109, 230503 (2012)
J. Niset, J. Fiurášek, and N. J. Cerf, “No-Go Theorem for Gaussian Quantum Error Correction,” Phys. Rev. Lett. 102, 120501 (2009)
J. Eisert, S. Scheel, and M. B. Plenio, “Distilling Gaussian States with Gaussian Operations is Impossible,” Phys. Rev. Lett. 89, 137903 (2002)
Y. O. Dudin, A. G. Radnaev, R. Zhao, J. Z. Blumoff, T. A. B. Kennedy, and A.Kuzmich, “Entanglement of Light-Shift Compensated Atomic Spin Waves with Telecom Light,” Phys. Rev. Lett. 105, 260502 (2010)

About the Authors

Monika Schleier-Smith is Assistant Professor of Physics at Stanford University. She received her Ph.D. in 2011 from the Massachusetts Institute of Technology and subsequently pursued postdoctoral research at the LMU Munich and Max Planck Institute of Quantum Optics. She is interested in elucidating connections between quantum information, quantum metrology, and many-body physics through experiments with ultracold atoms.

Haruka Tanji-Suzuki received her Ph.D. from Harvard University in 2011, studying strong photon-photon interaction mediated by atoms. After working on superconducting atom chip experiments at NTT Basic Research Laboratories (Japan) as a postdoc, she joined the Photon Science Center of the University of Tokyo and became a project research associate. Her current research interests include cavity quantum electrodynamics and quantum measurements using cold atoms.