A New Approach to the Matching Problem
Combinatorial optimization problems—of which the most famous is the traveling salesman problem—have traditionally belonged to the realms of computer science and mathematics, but in the last several decades, important contributions have also come from statistical physics. Physicists have developed a set of powerful mathematical tools to analyze models of systems with disorder and frustration, and it turns out that these methods can successfully be applied to optimization problems too [1]. In Physical Review E, Sergio Caracciolo at the University of Milan, Italy, and his colleagues used a new method inspired by problem solving in physics to investigate a classic problem in combinatorial optimization, called the Euclidean bipartite matching problem. They managed to compute the scaling function of the optimization problem; namely, how the cost of the optimal solution scales with the size and dimension of the system [2]. This function is an infinite series and while previous approaches have been able to figure out the first (leading) terms in the series, Carraciolo et al. are the first to be able to calculate the next (subleading) terms in the series. Their novel approach explores a connection between the discrete matching problem and a continuous optimization problem from the 18th century.
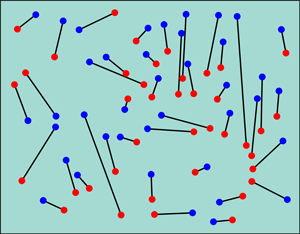
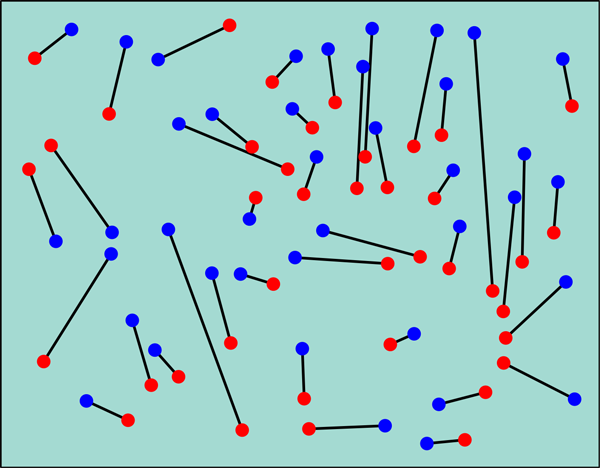
The Euclidean bipartite matching problem is best illustrated by an example. You are a sales manager for a company, and you have n salespeople on the road to meet customers. Your salespeople are currently located in n cities, and you want to relocate them to n new cities such that the total distance traveled by your sales force is minimized. You draw all 2n cities on a map and color the current locations of salespeople red and the new destinations blue. Your task is then to match the cities in red-blue pairs such that the sum of the red-blue distances in your matching is minimized (Fig. 1). The term bipartite in this matching problem refers to the fact that we are matching elements from two disjunctive sets (“red” and “blue” cities). In the general bipartite matching problem we are looking for a permutation π that minimizes the cost function E(π)=n-1∑ni=1wi,π(i), where wij denotes the cost of matching red element i with blue element j. In the Euclidean matching problem, wij is the geometrical distance between red city i and blue city j.
As algorithms go, the general bipartite matching problem is “easy” since we know efficient algorithms that can find solutions in polynomial time. But algorithms look at the problem case by case, they don’t tell us much about generic properties of optimal matchings. A simple example is the relation between the size n of the problem and the cost value of the optimal matching. For large values of n this scaling relation becomes independent of particular instances and represents a generic feature of the matching problem. In the case of the Euclidean matching problem, we expect that, given a red point, the nearest blue points can be found in a volume of order O(n-1) around it. Hence their distances from the red point are of order O(n-1/d) where d is the spatial dimension. Assuming that in an optimal matching, each red point is matched to one of its nearest neighbors, the optimal cost should scale like O(n-1/d). This is in fact the dominant (leading order) term of the scaling function for large values of n, at least for d>2 [3]. Carraciolo et al. go beyond this result by computing the subleading term of the scaling function.
The established mathematical tools of statistical physics work best if the costs wij can be considered independent random variables. But in the random Euclidean matching problem considered by Carraciolo et al., the random positions of the points in d-dimensional space are independent and the resulting distances wij are correlated random variables. Therefore Carraciolo et al. had to look for an alternative approach and they found one that is both simple and surprising [2]: they discard the discrete nature of the matching problem and resort to a continuous generalization for which an analytical expression for the minimum cost can be computed.
Again, an example will help to understand this continuous problem. Imagine that instead of sending salespeople from red to blue cities we want to move piles of sand to fill in holes (Fig. 2). The total volume of sand equals the total volume of holes, but the amount of sand varies from pile to pile, and the volume of the holes varies, too. The task is to minimize the total distance that is traveled by all the grains of sand. This problem is known as the Monge-Kantorovich transportation problem. It was introduced by Gaspard Monge in 1781 [4] as the problem of “excavation and embankments” (les déblais et les remblais).
Both piles of sand and holes are no longer characterized by points in space but by continuous distributions. And sand from one pile can go to different holes. The Monge-Kantorovich problem is a continuous generalization of the Euclidean bipartite matching problem, and, as such, it seems to be harder to analyze than the discrete version. But surprisingly, this is not the case.
The solution of the Monge-Kantorovich problem is trivial in the limiting case in which there is only one hole that spans the whole area, with constant depth, and sand that is uniformly distributed over the hole: we simply let each grain of sand fall down where it is. Caracciolo et al. start from this simple solution and consider the case of small deviations from the uniform distribution for both sand and holes. The continuous nature of the problem allows them to derive an analytical expression for the expected transportation cost in terms of the small deviations from the uniform distribution. (The approach is similar to the one used to analyze small transverse distortions of a continuous elastic membrane.) The mathematics involved is basically vector analysis, the Poisson equation, and Fourier transformation—very familiar grounds for physicists.
The authors then claim that in the large n limit, the discrete Euclidean matching problem is similar to the case of small deviations from the uniform distribution in the Monge-Kantorovich problem. This is a reasonable assumption since the cities in the random Euclidean matching problem are finite samples of the uniform distribution. The authors don’t specify the similarity in technical terms or even prove it. Rather, they boldly apply the formula from the continuous solution to the discrete case to obtain the asymptotic scaling of the random Euclidean bipartite matching problem in d dimensional space. Their approach reproduces the known leading order of the scaling function in all dimensions d and it also yields the complete subleading term for d>2 and the previously unknown constants in the leading order term for d=1 and d=2.
Switching from discrete to continuous variables is a common pattern in computer science to design powerful algorithms for optimization problems [5]. Caracciolo et al. demonstrate that this idea can also be used to analyze random instances of combinatorial optimization problems. Their results improve our knowledge about the scaling of the Euclidean matching problem. It remains to be seen whether their method can be extended to other optimization problems.
References
- M. Mezard, G. Parisi, and M. A. Virasoro, Spin glass theory and beyond, World Scientific Lecture Notes in Physics, Vol. 9.(World Scientific, Singapore, 1987)[Amazon][WorldCat]
- S. Caracciolo, C. Lucibello, G. Parisi, and G. Sicuro, “Scaling hypothesis for the Euclidean bipartite matching problem,” Phys. Rev. E 90, 012118 (2014)
- M. Talagrand, “Matching Random Samples in Many Dimensions,” Ann. Appl. Prob. 2, 846 1992
- G. Monge, in Histoire de l’Académie royale des sciences avec les mémoires de mathématique et de physique tirés de registres de cette Académie (1781) pp. 666-704
- C. Moore and S. Mertens, The Nature of Computation (Oxford University Press, Oxford, 2011)[Amazon][WorldCat]