Cool Physics with Warm Ions
Quantum computers are a hot topic in physics [1]. This is a bit ironic since most proposed ways to construct a quantum computer require cooling systems to nearly absolute zero because of the sensitivity of quantum algorithms to thermal fluctuations. Trapped ions have been one of the most successful platforms for quantum computing studies, due in part to laser cooling techniques that can conveniently cool ions to temperatures of a few microkelvin. However, as researchers contemplate more complex experiments involving ever-larger numbers of ions, the cooling process becomes more of a challenge as the number of degrees of freedom that need to be controlled grows quickly. A potential solution to this problem involves using ultrafast lasers, which can manipulate the quantum state of an ion so quickly that its temperature is irrelevant. Chris Monroe and colleagues [2] now demonstrate this utility by using fast pulses to implement precise quantum control of the state of a trapped ion over a wide range of temperatures, from 5 microkelvin (𝜇K) to 0.5 kelvin (K).
The need for low temperatures in quantum computing can be easily understood. Quantum computers work by putting a large collection of particles such as ions into specified collective quantum states, and this capability is what a quantum algorithm uses to obtain advantages over a classical analog. Such operations are only possible if the particles are in a well-defined state to begin with. In practice, that state might as well be the ground state, which would correspond to having the particles at nearly absolute zero temperature. Even with laser cooling techniques it is not easy to cool the motion of an ion sufficiently. However, the quantum states used for computing are typically internal states like spin states, and the relatively large energy splitting between spin states means that the spin temperature need not be so cold. The motion of the ions is still relevant, however, because it affects the Coulomb interactions between ions. Such interactions provide the coupling needed to form the collective quantum states required for quantum computing [3]. Therefore, thermal fluctuations in the motion will introduce uncertainty into the spin state and can spoil the computing algorithm. To avoid this, it is usually necessary for the ions to be cooled to a few microkelvin or lower [4].
The cooling requirement can be relaxed if the laser pulses used to control the ions are very short, since the ions are then effectively “frozen” during a pulse [5]. Standard pulsed-laser technology can produce pulses that are sufficiently short. In their study, Monroe and co-workers used pulses lasting 10 picoseconds to drive a spin-dependent kick, in which the pulse flips the spin of the ion at the same time as it delivers a momentum kick. The sign of the momentum kick depends on whether the spin flips from “up” to “down” or from “down” to “up,” so this procedure couples the ion’s spin and motional states and can thus provide a controlled interaction between the spins of different ions. The accuracy of this operation is over 99%, and thanks to the fast pulse it is essentially independent of the ion’s initial velocity.
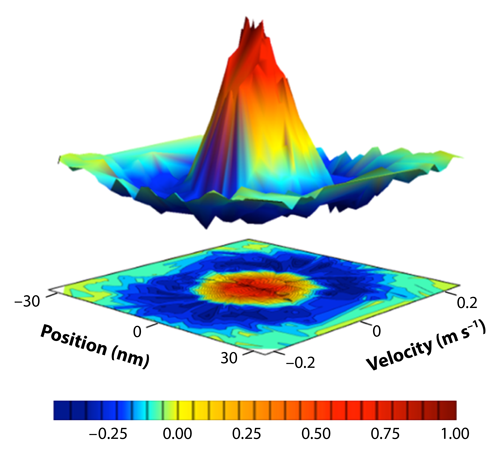
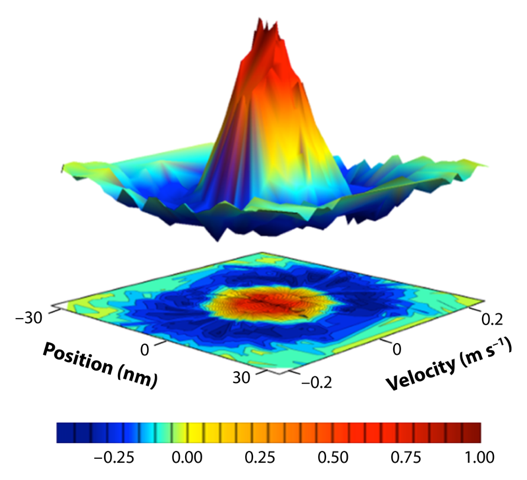
The authors here employed the spin-dependent kick to characterize the motion of the ion. By applying the operation to an ion in a quantum superposition of spin states, they produced a superposition of “kicked” and “unkicked” motional states. Each of these motional states evolves with a different quantum phase, and the difference in phases depends on the initial velocity of the ion. By later reversing the kicks and recombining the two parts of the superposition, the authors could determine the phase difference and thus the initial velocity. Because the initial velocity is itself a quantum variable, it has a quantum probability distribution function (Fig. 1), so it was necessary to repeat the experiment with a range of kick strengths and phase evolution times in order to map out this function. The process for doing this is known as quantum tomography and is relatively well understood [6]. In the past, quantum tomography has been limited to use with very cold ions, because the spin-dependent kick operation degraded at higher ion temperatures. Monroe and co-workers overcame this limitation with their pulsed-laser technique. The highest temperature measured was about 0.5K, and the authors estimate that temperatures of 100K or higher would be measurable without significant technological challenges. The lowest temperature was about 5𝜇K, near the limit of conventional laser cooling.
The velocity distribution measurements provide a precise estimate of the ion’s temperature when it is in thermal equilibrium. The method was also used to characterize a nonequilibrium state at an energy corresponding to about 50𝜇K, with the distribution shown in the figure. The accurate results obtained in all cases demonstrate that the pulsed-laser method is a powerful tool for state characterization. In the bigger picture, it illustrates that complex quantum manipulations such as spin-dependent kicks are not restricted to very cold ions. This ability relieves a significant constraint on future development of quantum computing methods.
That said, there are still important issues that must be resolved. Monroe and colleagues have convincingly shown that they can implement an accurate spin-dependent kick on a single ion regardless of temperature, but as noted, quantum computing requires the further step of coupling the spins of different ions. Although methods have been proposed to use pulsed lasers to entangle warm ions [7, 8], they have not yet been demonstrated. The authors’ results are a promising step in this direction, but whether a high-temperature quantum computer is possible remains uncertain.
This research is published in Physical Review Letters.
References
- T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe, and J. L. O’Brien, “Quantum Computers,” Nature 464, 45 (2010).
- K. G. Johnson, B. Neyenhuis, J. Misrahi, J. D. Wong-Campos, and C. Monroe, “Sensing Atomic Motion from the Zero Point to Room Temperature with Ultrafast Atom Interferometery,” Phys. Rev. Lett. 115, 213001 (2015).
- J. I. Cirac and P. Zoller, “Quantum Computations with Cold Trapped Ions,” Phys. Rev. Lett. 74, 4091 (1995).
- J. Eschner, G. Morigi, F. Schmidt-Kaler, and R. Blatt, “Laser Cooling of Trapped Ions,” J. Opt. Soc. Am. B 20, 1003 (2003).
- J. F. Poyatos, J. I. Cirac, R. Blatt, and P. Zoller, “Trapped Ions in the Strong-Excitation Regime: Ion Interferometry and Nonclassical States,” Phys. Rev. A 54, 1532 (1996).
- K. Banaszek, M. Cramer, and D. Gross, “Focus on Quantum Tomography,” New J. Phys. 15, 125020 (2013).
- J. J. García-Ripoll, P. Zoller, and J. I. Cirac, “Speed Optimized Two-Qubit Gates with Laser Coherent Control Techniques for Ion Trap Quantum Computing,” Phys. Rev. Lett. 91, 157901 (2003).
- L.-M. Duan, “Scaling Ion Trap Quantum Computation through Fast Quantum Gates,” Phys. Rev. Lett. 93, 100502 (2004).