History is Written by the Survivors
In the theory of evolution, fitness is not merely about survival; a species also has to reproduce. Bacteria that express a drug-resistant trait may outlive an exposure, but if this trait slows the growth of the cells, they may not be able to divide quickly, putting them at a disadvantage once the drug is removed. The fittest organisms therefore adopt traits that allow a trade-off between survival of an environmental stress and an ability to reproduce [1]. Evolutionary biologists quantify this fitness with a mathematical “reproductive function,” which depends on a selected trait (such as age) and whose height gives the probability that a species with that trait will survive and reproduce. This function can, for example, provide a useful metric in drug trials, and it could help evaluate the effects of environmental stresses—such as changing food supply or human intervention—on plants and animals. But determining it entails following thousands of individuals and monitoring their every reproduction and death event for extended periods of time. Guillaume Lambert from the University of Chicago and Edo Kussell from New York University demonstrate with experiments on bacteria that the same information can be obtained from a single surviving-cell lineage, the chain of offspring from an ancestor to a surviving cell [2]. This approach would make it possible to quickly assess, with far fewer measurements, the effects of an environmental stress in experimental trials.
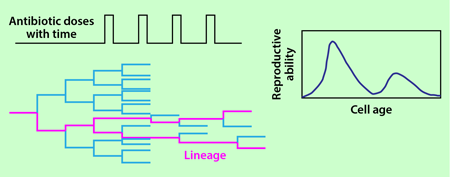
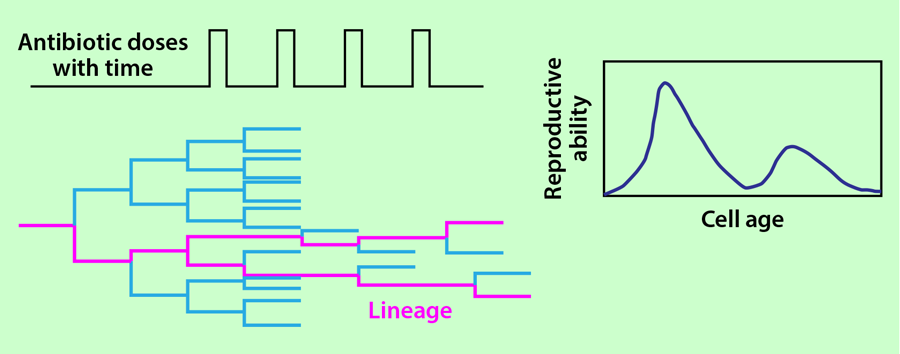
Lambert and Kussell rely on a theoretical framework, first introduced by Kussell and his colleagues in a previous publication [3], that makes a mathematical link between the age-dependent reproduction function for a population and that for a surviving lineage. Here’s the basic idea: The population size at time is simply the sum of the statistical weights of all possible lineages of length , known in physics as the “path integral.” The statistical weight of each lineage is determined by its growth rate. Under selection pressure, the surviving population is that which maximizes the integral and it’s therefore made of the optimal lineages with the maximal growth rate. In other words, the surviving population is dominated by the optimal lineages. As a result, the distribution of a selected trait (such as age) in the population is similar to that exhibited by the optimal lineage. Now, as the probability of a selected trait changes, so too will the growth rate of the population: this is because reproductive ability depends on the trait. The same is true in the optimal lineage. Hence, by measuring the population growth rate, and the selected trait distribution along one optimal lineage, one should be able to calculate the reproductive ability of cells as a function of the selected trait (the reproductive function). This is what Lambert and Kussell demonstrate experimentally for the case that an environmental stress selects for age in bacteria.
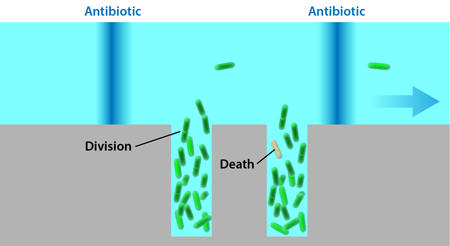
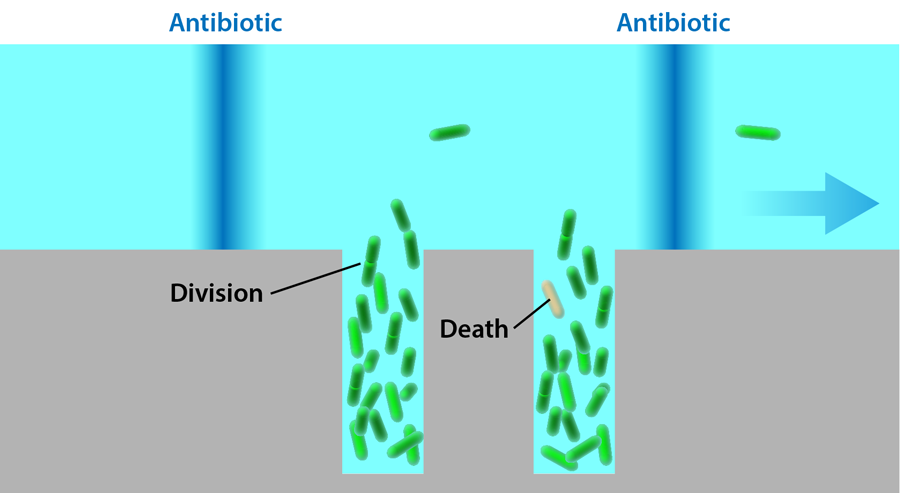
Lambert and Kussell study bacteria growing in a solution exposed to a cyclic dose of the antibiotic carbenicillin. The probability of cells dying when exposed to this drug increases with cell age, so the bacteria experience a life-history-dependent stress that isn’t constant, and its effects would normally be difficult to quantify without characterizing a large population for extended periods of time. The bacteria carry a plasmid that allows them to express a green fluorescent protein, which makes it possible to image their shapes and positions in a microscope. The cells are grown in a monolayer inside a flat rectangular microfluidic chamber, 7.5 micrometers wide and 50 micrometers long. One end of this chamber is left open and exposed to a perpendicular channel, through which nutrients flow. This setup, known as a microchemostat (Fig. 1), has been used in several different forms in the past [4,5] and allows precise control over the environment while maintaining the bacteria in each chamber at a fixed number. (When new cells are created, they push other cells into the flow channel, keeping the number of the cells inside the rectangular traps constant.)
The growth of the bacteria in a monolayer allows the researchers to monitor all of the cells simultaneously and detect every division and death event in the population. Fixed doses of carbenicillin are delivered to the bacteria for 20 minutes at 90-minute intervals through the flow channel. Each cell’s age is defined as the time since it formed in a division and is reset to zero when it divides again. The reproductive ability of cells at age is calculated as twice the division rate at which cells of that age divide, multiplied by the probability of the cell to survive to that age.
Lambert and Kussell collected data from 18 different populations grown in this setup and calculated the average reproductive ability of the cells as a function of their age after 25 cycles of antibiotic treatment. In each population, they also selected a single lineage that survived the 25 cycles of antibiotic treatment and calculated the age distribution in the lineages (Fig. 2). This distribution was then used to infer the reproductive ability of the cell as a function of its age following the theory of Kussell et al. [3]. The authors show that the reproductive functions calculated from all the individuals in the population and from a single lineage have an excellent degree of overlap.
One limitation of this approach is that a lineage would need to be followed for a very long time if the environmental change was slow. Also, which lineage to follow isn’t known at the start of the experiment, so all of the organisms have to be followed until the experiment is complete. But having a theoretical framework that establishes a link between lineage and population statistics can have ample applications. With a significantly smaller number of measurements, scientists could deduce quantitative information about the influence of selective environmental pressures on the fitness of microorganisms. For example, it can be used in drug trials to determine the survival probability of bacteria under different conditions or patterns of drug application. These results imply also that if an organism’s lineage can be traced far enough back in time, one can deduce important quantitative information about the environmental conditions that influenced its evolution. Marine biologists could, for example, use this method to analyze how fishing practices affect certain fish populations or traits in the population, such as size. In addition, the quantitative aspect of these measurements will enable us to develop theoretical models that can be tested experimentally and help us better understand and characterize evolutionary processes and their consequences.
This research is published in Physical Review X.
References
- S. Leibler and E. Kussell, “Individual Histories and Selection in Heterogeneous Populations,” Proc. Natl. Acad. Sci. U. S. A. 107, 13183 (2010)
- Guillaume Lambert and Edo Kussell, “Quantifying Selective Pressures Driving Bacterial Evolution Using Lineage Analysis,” Phys. Rev. X 5, 011016 (2015)
- Y. Wakamoto, A. Y. Grosberg, and E. Kussell, “Optimal Lineage Principle for Age-Structured Populations,” Evolution 66, 115 (2012)
- P. Wang, L. Robert, J. Pelletier, W. L. Dang, F. Taddei, A. Wright, and S. Jun, “Robust Growth of Escherichia coli,” Curr. Biol. 20, 1099 (2010)
- J. E. Keymer, P. Galajda, C. Muldoon, S. Park, and R. H. Austin, “Bacterial Metapopulations in Nanofabricated Landscapes,” Proc. Natl. Acad. Sci. U. S. A. 103, 17290 (2006)