A Boost for Superconducting Logic

Jason Robinson

Viewpoint

A Boost for Superconducting Logic

Jason Robinson

Department of Materials Science & Metallurgy, University of Cambridge, 27 Charles Babbage Road, CB2 0FS, United Kingdom

May 26, 2015• Physics 8, 49

A new choice of materials leads to more practically useful superconducting spin valves.

Figure caption — **Figure 1:** In the superconducting spin valves engineered by Aarts and colleagues, the relative alignment of two ferromagnets ( ${CrO}_{2}$ , in purple; Ni, in orange) determines the transition temperature $(T_{c})$ of a superconductor layer (MoGe, in grey). (Top) When the magnetizations are parallel (or antiparallel), only electron pairs with antiparallel spins (“singlet pairs”) can leak into the Ni layer, and these pairs cannot enter ${CrO}_{2}$ because this material is fully spin polarized. (Bottom) When the magnetizations are misaligned, singlet pairs can transform into equal-spin triplet pairs, which can, in turn, leak into the ${CrO}_{2}$ . This extra leakage suppresses superconductivity further, and lowers $T_{c}$ . The suppressions is greatest when the misalignment angle is $90^{\circ}$ .

The key component of state-of-the-art magnetic memories and sensors is a device called a spin valve, whose electrical resistance depends on the relative alignment of the magnetizations of two thin ferromagnetic elements. Researchers are interested in developing superconducting analogs of the spin valve to be used in “cryogenic memory” technologies that consume little power and dissipate little heat. In this case, changing the relative alignment of the two ferromagnets shifts the transition temperature $(T_{c})$ of an adjacent thin superconducting layer—an effect that can be used to turn the superconducting state on (or off) and lower (or raise) the device’s total resistance. But so far, the $T_{c}$ shifts observed in experiments have been too small for practical use. Jan Aarts and his colleagues at Leiden University in the Netherlands demonstrate superconducting spin valves in which $T_{c}$ changes by nearly $1 K$ [1], an order of magnitude increase compared to previous schemes.

In ferromagnetic metals, an internal exchange field generates an imbalance in the number of electrons with “up” and “down” spins. An electrical current that passes through a ferromagnet will therefore carry a net spin, in addition to charge, with the majority of spins (the majority state) pointing parallel to the magnetization and the minority (the minority state) antiparallel. Such spin-polarized currents are utilized for logic and sensor applications, and finding efficient and practical ways to generate and control them is a major goal of spintronics.

The most famous spintronic device is the spin valve. In its simplest form, the spin valve is a ferromagnet/normal metal/ferromagnet ( $F / N / F$ ) multilayer. Electrons in the majority spin state scatter less when the two $F$ layers are parallel than when they are antiparallel, so the parallel configuration has a lower resistance. This “giant magnetoresistance” (GMR) effect was recognized with the 2007 Nobel prize in physics and is the basis for read heads in magnetic hard drives.

Even predating the discovery of GMR, Pierre de Gennes [2]—and later other theorists [3–5]—proposed the superconducting spin valve. This layered structure consists of either a thin superconducting layer ( $S$ ) between two ferromagnets ( $F / S / F$ ) [2–4] or a superconducting layer stacked on top of two ferromagnets ( $F / F / S$ ) [5]. Even though the charge carriers in most superconductors are pairs of electrons with opposite spin (spin singlets) and do not carry a net spin, the $T_{c}$ of the superconductor in a spin valve can depend on the magnetization alignment of the ferromagnetic layers. This results from the so-called superconductor proximity effect, which involves the leakage of paired electrons from the $S$ layer into the neighboring $F$ layers, suppressing superconductivity so that it occurs at a lower $T_{c}$ .

In 2002, Gu et al. demonstrated this superconducting spin-valve effect using $F / S / F$ devices [6], but the measured difference in $T_{c}$ ( $Δ T_{c}$ ) between the configuration with the $F$ layers antiparallel and parallel was less than $10$ millikelvin (mK), which is comparable to the width of the transition and far too small for practical superconducting switches. Quasiclassical theory, however, predicts larger values of $Δ T_{c}$ that can be a significant fraction of $T_{c}$ . Despite extensive experimental research on the superconducting spin-valve effect, researchers have yet to achieve values of $Δ T_{c} / T_{c}$ that are large enough for practical applications.

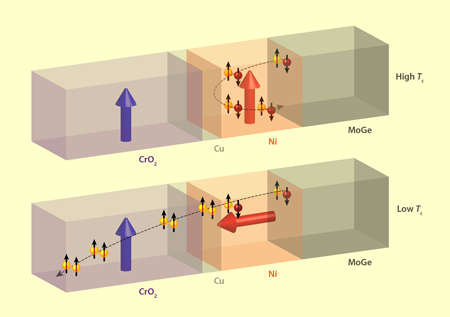
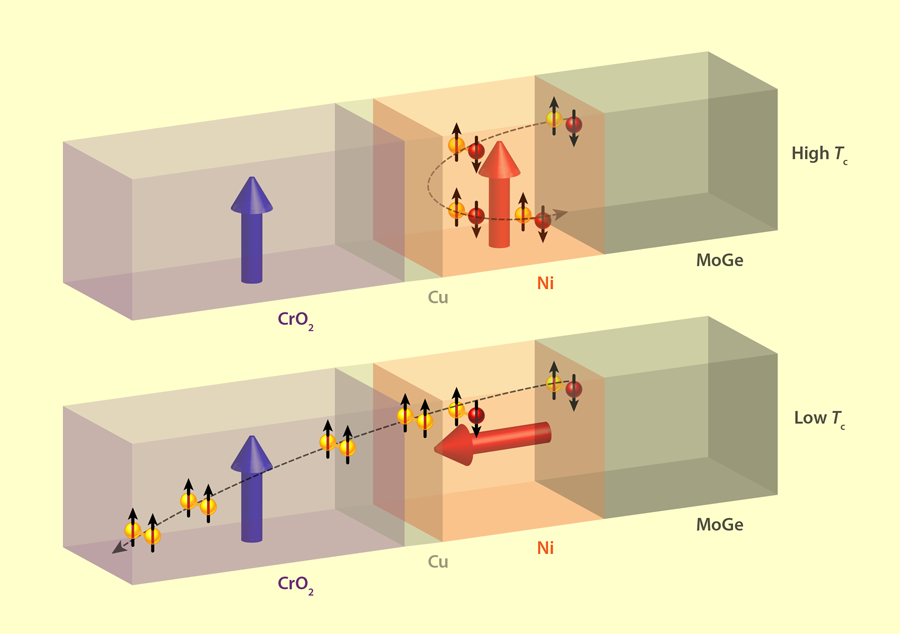
In their devices (Fig.1), Aarts and his colleagues take advantage of a particular kind of superconductor proximity effect that involves the conversion of singlet pairs to triplet pairs with parallel spins (equal-spin triplet pairs). Singlet to triplet pair conversion occurs when the paired electrons in a superconductor encounter an interface with an inhomogenous magnetic field [7,8]. On encountering a ferromagnetic exchange field, singlet pairs gain a net momentum (spin mixing), which results first in the creation of zero-spin triplets, that is, pairs with a zero-spin projection along the magnetization axis. Unlike singlet pairs, zero-spin triplets can exist in different forms as their spin projection depends on the orientation of the magnetization-quantization axes. And if the zero-spin triplet pairs encounter a second ferromagnetic layer that is misaligned with the ferromagnetic layer where they were formed, the different triplet components can transform into each other. This spin-rotation process favors the generation of equal-spin triplet pairs and enhances the proximity effect that suppresses superconductivity and reduces $T_{c}$ . In 2010, theorists proposed the effect could be used to engineer a spin-valve effect in $F / F / S$ structures [9]. With the two $F$ layers misaligned by $90^{\circ}$ , the magnetization would be maximally inhomogenous, causing $T_{c}$ to drastically dip relative to its value when the $F$ layers were aligned parallel or antiparallel.

Although this behavior had been experimentally observed in $F / F / S$ devices using metallic ferromagnets [10,11], the largest reported suppression of $T_{c}$ was only about $120 mK$ [11]. Aarts and his colleagues achieved a much larger suppression because of a clever choice of material for one of the $F$ layers. Their devices consist of ${CrO}_{2} /Cu/Ni/MoGe$ layers (Fig.1) where ${CrO}_{2}$ and Ni are ferromagnetic layers sandwiching a nonmagnetic spacer (Cu), and MoGe is a singlet superconductor with a $T_{c}$ of $\sim 6$ K. Unlike metallic ferromagnets, which are only partially spin polarized, ${CrO}_{2}$ is a half-metallic ferromagnet whose electrons at the Fermi energy are 100% spin polarized. This means that scattering processes that “flip” the spin of an electron don’t occur in ${CrO}_{2}$ . As a result, spin-polarized triplet pairs can travel much further away from the superconducting layer than is possible in metallic ferromagnets. This enhances the superconductor proximity effect and leads to larger differences in $T_{c}$ between aligned and misaligned ferromagnetic states. Using a magnetic field to rotate the Ni ferromagnetic layer, the researchers were able to shift $T_{c}$ by $1$ K.

The discovery that half-metallic ferromagnets are the secret to a large suppression in $T_{c}$ is an exciting opportunity for the development of magnetization-controlled superconducting switches. This is because the $T_{c}$ varies over a wide temperature range, meaning that the resistance state of the device is highly stable to temperature fluctuations. Triplet superconducting spin-valves can perform almost the equivalent logical functions as GMR devices (albeit at lower temperatures), but with potentially much greater energy efficiency as dissipation is minimised by the presence of superconductivity. The results from Aarts and colleagues therefore motivate the study of more complex devices that combine nonequilibrium spin transport and superconducting phase coherence. Such devices could be used to control the magnetic state of superconducting spin valves, and potentially the flow of heat, but electrically, instead of with magnetic fields.

This research is published in Physical Review X.

References

A. Singh, S. Voltan, K. Lahabi, and J. Aarts, “Colossal Proximity Effect in a Superconducting Triplet Spin Valve Based on the Half-Metallic Ferromagnet CrO $_{2}$ ,” Phys. Rev. X 5, 021019 (2015)
P. G. De Gennes, “Coupling between Ferromagnets through a Superconducting Layer,” Phys. Lett. 23, 10 (1966)
L. R. Tagirov, “Low-Field Superconducting Spin Switch Based on a Superconductor/Ferromagnet Multilayer,” Phys. Rev. Lett. 83, 2058 (1999)
A. I. Buzdin, A. V. Vedyayev, and N. V. Ryzhanova, “Spin-Orientation-Dependent Superconductivity in $F / S / F$ Structures,” Eur. Phys. Lett. 48, 686 (1999)
S. Oh, D. Youm, and M. R. Beasley, “A Superconductive Magnetoresistive Memory Element Using Controlled Exchange Interaction,” Appl. Phys. Lett. 71, 2376 (1997)
J. Y. Gu, C.-Y. You, J. S. Jiang, J. Pearson, Ya. B. Bazaliy, and S. D. Bader, “Magnetization-Orientation Dependence of the Superconducting Transition Temperature in the Ferromagnet-Superconductor-Ferromagnet System: CuNi/Nb/CuNi,” Phys. Rev. Lett. 89, 267001 (2002)
F. S. Bergeret, A. F. Volkov, and K. B. Efetov, “Long-Range Proximity Effects in Superconductor-Ferromagnet Structures,” Phys. Rev. Lett. 86, 4096 (2001)
J. Linder and J. W. A. Robinson, “Superconducting Spintronics,” Nature Phys. 11, 307 (2015)
Ya. V. Fominov, A. A. Golubov, T. Yu. Karminskaya, M. Yu. Kupriyanov, R. G. Deminov, and L. R. Tagirov, “Superconducting Triplet Spin Valve,” JETP Lett. 91, 308 (2010)
P.V. Leksin, N.N. Garif’yanov, I. A. Garifullin, Ya. V. Fominov, J. Schumann, Y. Krupskaya, V. Kataev, O. G. Schmidt, and B. Büchner, “Evidence for Triplet Superconductivity in a Superconductor-Ferromagnet Spin Valve,” Phys. Rev. Lett. 109, 057005 (2012)
X. L. Wang, A. Di Bernardo, N. Banerjee, A. Wells, F. S. Bergeret, M. G. Blamire, and J. W. A. Robinson, “Giant Triplet Proximity Effect in Superconducting Pseudo Spin Valves with Engineered Anisotropy,” Phys. Rev. B 89, 140508 (2014)

About the Author

Jason Robinson is a University Lecturer in the Department of Materials Science and Metallurgy in the University of Cambridge and is a University Research Fellow of the Royal Society. He received his Ph.D. in 2007 at the University of Cambridge. His research group explores spin transport in nanoscale devices and in thin film heterostructures, which include interface coupling of materials with radically different properties such as magnetism and superconductivity.