Polarizing Nuclear Spins in Silicon Carbide

Paola Cappellaro

Viewpoint

Polarizing Nuclear Spins in Silicon Carbide

Research Laboratory of Electronics and Department of Nuclear Science and Engineering,Massachusetts Institute of Technology, Cambridge, MA 02139, USA

June 17, 2015• Physics 8, 56

An optical technique polarizes the spin of nuclei in silicon carbide, offering a potential new route to nuclear spin-based quantum memory.

Figure caption — **Figure 1:** (Left) The crystal structure of silicon carbide (silicon in gold, carbon in silver) supports different types of defects, called color centers. The one shown here consists of a silicon vacancy and a carbon vacancy. The color center attracts electrons (shown in green), which have a strong hyperfine interaction with nearby silicon nuclei, whose spins are initially nonpolarized. (Right) After optical illumination, the electronic spin in the color center is polarized. With careful tuning of an external magnetic field, this polarization flows into the nearby nuclear spin.

Quantum computers and other quantum information processing (QIP) devices—such as simulators, sensors, and communication channels—hold the promise to deliver performances not attainable by classical systems. Unfortunately, the qubits used to store information are usually fragile and difficult to manipulate and engineer, thus forestalling advances in the field. Many qubit candidates suffer from short coherence times due to interactions with the environment. In this regard, spin- $1 / 2$ nuclei are an attractive qubit system, as they are quite insensitive to external degrees of freedom that cause decoherence. However, this insensitivity also makes it challenging to initialize and manipulate nuclear spins. An international team of researchers led by David Awschalom of the University of Chicago, Illinois, has managed to polarize nuclear spins in silicon carbide ( $SiC$ ) using optical light [1]. This is not the first time this sort of spin control has been demonstrated, but compared to previous materials, SiC has many practical advantages, such as being inexpensive to grow and fabricate into tiny structures. The results are therefore an important step in making nuclear spins a viable contender for scalable quantum computation.

Nuclear spins were one of the first systems used to demonstrate that quantum computation could be achieved in practice [2], taking advantage of the good control techniques developed in nuclear magnetic resonance (NMR). However, nuclear spins have several drawbacks. For one, individual nuclear spins cannot be spatially addressed and detected with conventional inductive techniques used in NMR, so spins are addressed by their frequencies, which only offers a limited number of distinct qubits. In addition, nuclear spins are typically found in a thermal mixture state, whereas a well-defined pure state is desirable as the initial state for many QIP applications. Because of these reasons, NMR-based QIP—despite many early achievements—is considered less promising for scalable quantum computation than other quantum systems.

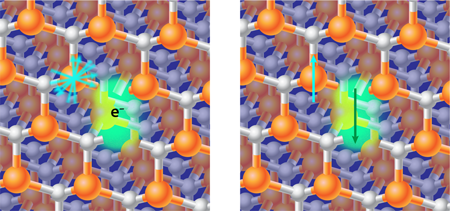
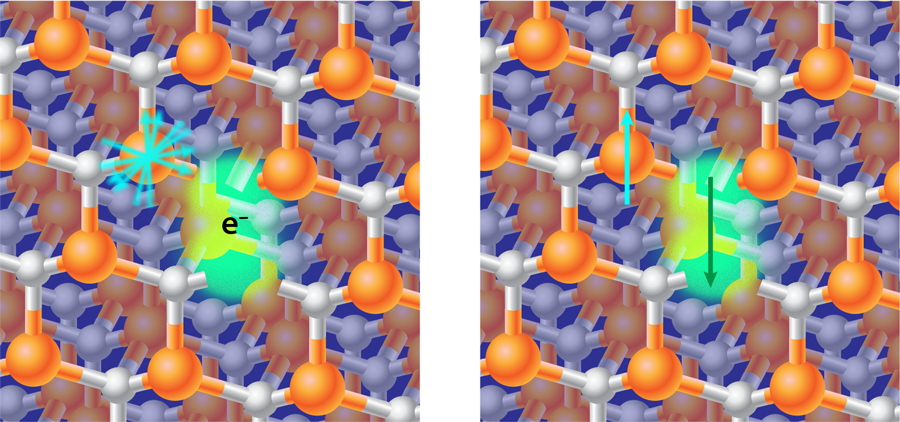
The experiment of Awschalom and co-workers could help to ease some doubts about the viability of nuclear spins in QIP applications [1]. The team managed to polarize silicon nuclear spins in $SiC$ to a level of about $99 %$ , which corresponds to an effective spin temperature of 5 microkelvin (the sample as a whole remains at room temperature). To achieve this result, the researchers exploited the strong hyperfine interaction of these nuclear spins to defects in the crystal lattice called “color centers.” Color centers are point defects in the crystal structure (see Fig. 1) that can trap electrons or holes. The electronic ground state can absorb and reemit visible light, thus giving a color to the otherwise transparent material. These color centers also possess an electronic spin that interacts with external magnetic fields via the Zeeman effect and with the nearby nuclear spins through the hyperfine interaction.

The researchers started with $SiC$ wafers intentionally grown with color centers. They placed their samples in a magnetic field and illuminated them with infrared light, which polarized the color center electronic spins. This polarization corresponds to cooling the spins to their ground state. Normally, the polarization of electronic spins would have little effect on the nuclear spins because of their different Zeeman energy. A change (or flip) in the electron spin couldn’t energetically be compensated for by a nuclear spin flip. However, the authors were able to allow these spin flip-flops by tuning the external magnetic field. For field values of around $400$ gauss, the Zeeman energy of the electronic spins is counterbalanced by their intrinsic zero-field energy, so that spin flips for electrons and nuclei have nearly the same energy. This allows a flow of polarization from the cold electronic spins to the hot nuclear spins. The researchers could thus achieve very high polarization and prepare the nuclear spins in their ground state with an accuracy of $\sim 99.5 %$ .

Polarizing nuclear spins by arranging thermal contact with electronic spins is often used to increase the sensitivity of ensemble NMR experiments [3]. The well-established technique, which is referred to as dynamic nuclear polarization, usually requires low temperatures and microwave driving, but optical polarization of nuclear ensembles has also been achieved in the past [4]. Only recently, however, have researchers managed to achieve high local polarization of nuclear spins. Like the current study, these works have taken advantage of electronic spin defects in silicon, antimony, and diamond [5]. These systems offer the ability to initialize, control, and read out individual nuclear spins. The nuclear spin qubits can thus be exploited as long-lived quantum memory, with coherence times greater than $1$ second for single carbon nuclei in diamond, $30$ seconds for single phosphorous nuclei in silicon, and $39$ minutes for an ensemble of phosphorous nuclei in silicon [6]. These record-breaking coherence times, together with the ability to implement precise and efficient control on individual nuclear spins, open a new realm of possibilities for quantum technologies. Quantum registers based on nuclear spins have already been used to perform small algorithms that can test fundamental questions in quantum mechanics, implement quantum error correction, or improve the performance of quantum sensors [7].

Awschalom and co-workers have built on these results to bring quantum devices one step closer to a practical and convenient realization by using a host material, silicon carbide, that is device-friendly. $SiC$ can be grown into high-quality single crystals by large-scale production and is popular in electronics applications where high temperature or high power is required [8]. Compared to diamond, a material that has recently been proposed as a host for electronic-nuclear spin qubits, $SiC$ is more amenable to nanofabrication. Indeed, it has been used in micro- and nanoelectromechanical systems, while $SiC$ nanostructures (quantum dots, photonic crystals, nanopillars, etc.) have elicited much interest for their potential use in photonic applications and optoelectronics [9]. Fast progress has also been made to characterize the numerous optically active paramagnetic defects that can occur in $SiC$ [10].

$SiC$ is thus fast positioning itself as one of the most promising materials for quantum devices, combining the ability to engineer nanostructures with the presence of paramagnetic quantum spin defects. Importantly, the work by Awschalom and colleagues demonstrates another key ingredient, the presence of an intrinsic memory associated with the nuclear spin. While there are still many challenges to quantum technologies, silicon carbide and its nuclear spins are poised to play an important role in overcoming them and bringing practical devices to reality.

This research is published in Physical Review Letters.

References

Abram L. Falk, Paul V. Klimov, Viktor Ivády, Krisztián Szász, David J. Christle, William F. Koehl, Ádám Gali, and David D. Awschalom, “Optical Polarization of Nuclear Spins in Silicon Carbide,” Phys. Rev. Lett. 114, 247603 (2015)
D. G. Cory, A. F. Fahmy, and T. F. Havel, “Ensemble Quantum Computing by NMR Spectroscopy,” Proc. Natl. Acad. Sci. U.S.A. 94, 1634 (1997); I. L. Chuang, L. M. K. Vandersypen, X. Zhou, D. W. Leung, and S. Lloyd, “Experimental Realization of a Quantum Algorithm,” Nature 393, 143 (1998)
A. Abragam and M. Goldman, “Principles of Dynamic Nuclear Polarization,” Rep. Prog. Phys. 41, 395 (1978)
M. A. Bouchiat, T. R. Carver, and C. M. Varnum, “Nuclear Polarization in He $^{3}$ Gas Induced by Optical Pumping and Dipolar Exchange,” Phys. Rev. Lett. 5, 373 (1960)
A. Yang, M. Steger, T. Sekiguchi, M. L. W. Thewalt, T. D. Ladd, K. M. Itoh, H. Riemann, N. V. Abrosimov, P. Becker, and H.-J. Pohl, “Simultaneous Subsecond Hyperpolarization of the Nuclear and Electron Spins of Phosphorus in Silicon by Optical Pumping of Exciton Transitions,” Phys. Rev. Lett. 102, 257401 (2009); R. Fischer, C. O. Bretschneider, P. London, D. Budker, D. Gershoni, and L. Frydman, ”Bulk Nuclear Polarization Enhanced at Room Temperature by Optical Pumping,” Phys. Rev. Lett. 111, 057601 (2013)
P. C. Maurer et al., “Room-Temperature Quantum Bit Memory Exceeding One Second,” Science 336, 1283 (2012); J. T. Muhonen et al., “Storing Quantum Information for 30 seconds in a Nanoelectronic Device,” Nature Nanotech. 9, 986 (2014); K. Saeedi, S. Simmons, J. Z. Salvail1, P. Dluhy, H. Riemann, N.V. Abrosimov, P. Becker, H.-J. Pohl, J. J. L. Morton, and M. L. W. Thewalt, “Room-Temperature Quantum Bit Storage Exceeding 39 Minutes Using Ionized Donors in Silicon-28,” Science 342, 830 (2013)
R. E. George, L. M. Robledo, O. J. E. Maroney, M.S. Blok, H. Bernien, M. L. Markham, D. J. Twitchen, J. J. L. Mortone, G. A. D. Briggs, and R. Hanson, “Opening Up Three Quantum Boxes Causes Classically Undetectable Wavefunction Collapse,” Proc. Natl. Acad. Sci. U.S.A. 110, 3777 (2013); G. Waldherr et al., “Quantum Error Correction in a Solid-State Hybrid Spin Register,” Nature 506, 204 (2014); A. Ajoy, U. Bissbort, M. D. Lukin, R. L. Walsworth, and P. Cappellaro, “Atomic-Scale Nuclear Spin Imaging Using Quantum-Assisted Sensors in Diamond,” Phys. Rev. X 5, 011001 (2015)
D. Nakamura, I. Gunjishima, S. Yamaguchi, T. Ito, A. Okamoto, H. Kondo, S. Onda, and K. Takatori, “Ultrahigh-Quality Silicon Carbide Single Crystals,” Nature 430, 1009 (2004)
C. A. Zorman and R. J. Parro, “Micro- and Nanomechanical Structures for Silicon Carbide MEMS and NEMS,” Phys. Status Solidi (b) 245, 1404 (2008); B.-S. Song, S. Yamada, T. Asano, and S. Noda, “Demonstration of two-dimensional photonic crystals based on silicon carbide,” Opt. Express 19, 11084 (2011)
S. Castelletto, B. C. Johnson, and A. Boretti, “Quantum Effects in Silicon Carbide Hold Promise for Novel Integrated Devices and Sensors,” Adv. Opt. Mater. 1, 609 (2013)

About the Author

Paola Cappellaro is the Esther and Harold Edgerton Associate Professor of Nuclear Science and Engineering at the Massachusetts Institute of Technology, where she leads the Quantum Engineering Group. She received her Ph.D. in 2006 from MIT and held a postdoctoral fellowship at Harvard University in the Institute for Theoretical Atomic, Molecular and Optical Physics. Her research focuses on understanding and exploiting quantum systems, in particular isolated spin defects, for applications in quantum information processing, sensing and imaging.