Watching Quasicrystals Grow
The initial discovery in 1984 [1] that certain metallic alloys can possess rotational symmetries forbidden in crystals, such as the symmetry of the regular icosahedron, raised a host of questions about these so-called quasicrystalline materials, or quasicrystals for short. Can the forbidden symmetries of quasicrystals be reconciled with their ability to form x-ray diffraction patterns with sharp spots? Can quasicrystals form faceted polyhedral shapes? Are they thermodynamically stable? These questions and many more have largely been answered over the subsequent decades, and in 2011 Daniel Shechtman was awarded the Nobel Prize in chemistry for the discovery of quasicrystals [2]. However, because quasicrystals have long-range but nonperiodic order, one of the most perplexing questions about them continues to be, “How do quasicrystals grow?” Theoretical models and computer simulations have made important advances on this front [3–6], but experimental answers to this question have been elusive. Using in situ high-resolution transmission electron microscopy (HRTEM), Keiichi Edagawa and colleagues [7] at the University of Tokyo and Tohoku University have now successfully observed—at the atomic scale—quasicrystals in the act of growing.
For centuries, crystals have been understood, indeed defined, to be composed of a single building block, or “unit cell,” that is copied and stacked together to form the entire three-dimensional crystal structure. The unit cell has been the foundational concept of crystallography from which models and theoretical frameworks have been developed to understand crystals and all of their properties. In particular, our comprehension of the ability of crystals to diffract x rays has—since the pioneering work of Walter Friedrich, Paul Knipping, and Max von Laue in 1912 [8]—been dependent on the long-range, periodic translational symmetry generated by the stacking of unit cells.
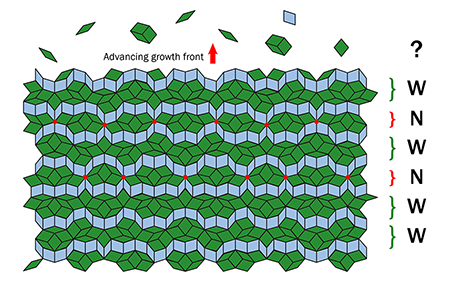
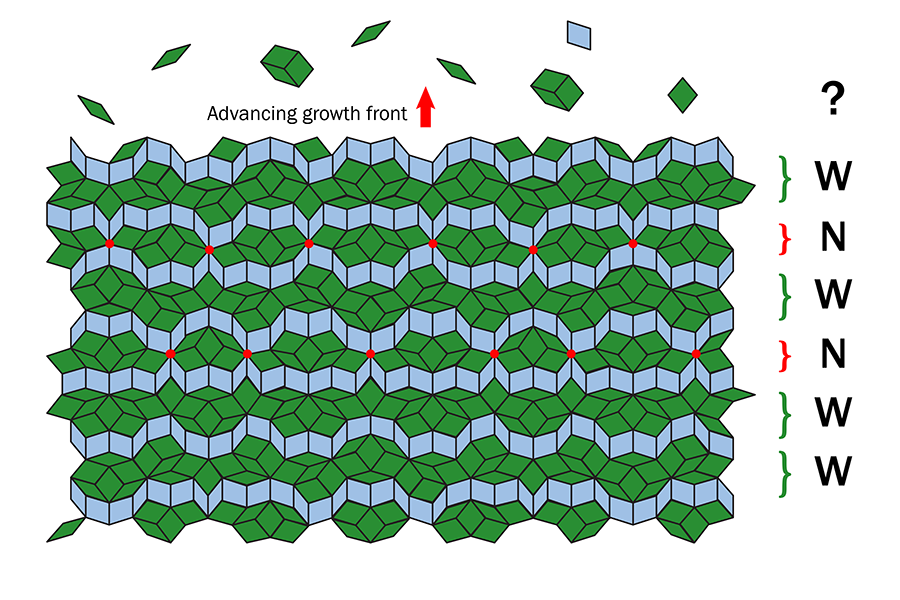
The structures of quasicrystals, on the other hand, can be modeled based on the famous Penrose tilings—nonperiodic arrangements that have not just one but two unit cells. But there is a dilemma in our understanding of quasicrystal formation. Crystals are built from the repetition of a single unit cell, so only local interactions between atoms are necessary to understand how they might grow. The long-range but nonperiodic order of perfect quasicrystals seems, however, to be significantly more difficult to build, tile-by-tile, using only local interactions. Consider, for example, the tile attachment in a quasiperiodic direction in the Penrose tiling (Fig. 1). Along the quasicrystal growth direction, the ideal tiling has a sequence of wide (W) and narrow (N) rows of tiles, where W and N are arranged in the predictable but nonperiodic fashion of a so-called Fibonacci sequence. To create a Fibonacci sequence, start with the short sequence WN and generate a new sequence following the replacement rules W WN and N W, yielding WNW. Subsequent application of these replacement rules to a prior sequence systematically generates a still longer Fibonacci sequence, such as WNWWN and WNWWNWNW (Fig. 1 illustrates part of this latter sequence). But what mechanism ensures that new layers of tiles attach in this specific way during growth? Therein lies the dilemma.
Edagawa and co-workers imaged the growth of a grain in a poly-grained sample of a quasicrystal made of aluminum, nickel, and cobalt ( ). The quasicrystal has crystallographically forbidden decagonal, or tenfold, rotational symmetry; in a rotation by 360° the structure repeats itself every 360°/10 of rotation, so it looks identical 10 times. The structure is composed of layers of two-dimensional Penrose tilings stacked periodically along the rotational symmetry axis. Using HRTEM and a heating stage to control the temperature, the authors heated the sample to 1183 K to enable the imaged quasicrystal grain to grow at the expense of a neighboring, shrinking grain. A movie of the growth process was digitally recorded in situ, and a time-series of images was extracted for analysis. By aligning the rotational symmetry axis of the growing grain with the direction of the HRTEM electron beam, the researchers could identify the positions of columns of atoms in the growing grain’s decagonal structure as a pattern of white dots on a black background. The shrinking grain, on the other hand, had no special orientation relative to the electron beam’s direction, and was visible only as a plain bright image.
Edagawa and colleagues constructed a tiling using the white dots of the growing grain and analyzed the resulting patterns with mathematical methods that are also used to make and study ideal quasicrystal tilings. This process allowed the authors to show that the growing grain displayed the structure of a nearly perfect quasicrystal tiling. At the growth front between the grains, however, they found that atomic clusters were commonly added in orientations corresponding to rows of tiles being flipped, breaking the ideal long-range quasiperiodic order. In the sequence of W and N rows, these growth errors correspond to an N layer being added at the growth front where the layer should have been W. But this form of disorder, called phason strain, was found to relax by subsequent rearrangements of these tiles—thus correcting the preceding growth error—sometimes even after several rows were added incorrectly. The researchers further observed that the phason strain relaxation times depended strongly on temperature, ranging from approximately 1 second at 1183 K to 10 to 20 seconds at 1123 K.
Edagawa and colleagues’ results indicate that near-ideal quasicrystal growth, at least in this decagonal phase, takes place via phason strain “error-and-correction” events near the growth front. Although it is still not clear what mechanisms drive the initial growth errors and their subsequent correction, this work may guide and refine theories and simulations aimed at understanding the detailed thermodynamic and atomic-scale mechanisms for ideal quasicrystal growth. It will also be interesting to test whether the authors’ observations apply to other quasicrystal phases, especially the icosahedral phases, which are quasiperiodic in three dimensions rather than two, as is the case for the decagonal phase. More directly, the present findings may help resolve a puzzle related to the recently discovered naturally occurring Al-Ni-Fe decagonal quasicrystal: evidence that this quasicrystal was rapidly quenched during its formation seems to be inconsistent with this phase’s apparent absence of phason strain, which instead “suggests a slow quench” (see Ref. [9]). Based on Edagawa and co-workers’ new results, there is reason to believe that the growth of ideal quasicrystals may be possible at quenching rates higher than expected through phason-strain relaxation at the growth front.
This research is published in Physical Review Letters.
References
- D. Shechtman, I. Blech, D. Gratias, and J. W. Cahn, “Metallic Phase with Long Range Orientational Order and No Translation Symmetry,” Phys. Rev. Lett. 53, 1951 (1984).
- http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2011/advanced-chemistryprize2011.pdf .
- U. Grimm and D. Joseph, “Modeling Quasicrystal Growth,” in Quasicrystals: An Introduction to Structure, Physical Properties and Applications, edited by J. B. Suck, M. Schreiber, and P. Häussler (Springer, Berlin, 2002), p. 199[Amazon][WorldCat].
- T. Dotera, T. Oshiro, and P. Ziherl, “Mosaic Two-Lengthscale Quasicrystals,” Nature 506, 208 (2014).
- C. V. Achim, M. Schmiedeberg, and H. Löwen, “Growth Modes of Quasicrystals,” Phys. Rev. Lett. 112, 255501 (2014).
- M. Engel, P. F. Damasceno, C. L Phillips, and S. C. Glotzer, “Computational Self-Assembly of a One-Component Icosahedral Quasicrystal,” Nature Mater. 14, 109 (2015).
- K. Nagao, T. Inuzuka, K. Nishimoto, and K. Edagawa, “Experimental Observation of Quasicrystal Growth,” Phys. Rev. Lett. 115, 075501 (2015).
- http://www.iucr.org/publ/50yearsofxraydiffraction/full-text/laues-discovery.
- L. Bindi, N. Yao, C. Lin, L. S. Hollister, C. L. Andronicos, V. V. Distler, M. P. Eddy, A. Kostin, V. Kryachko, G. J. MacPherson, W. M. Steinhardt, M. Yudovskaya, and P. J. Steinhardt, “Natural Quasicrystal with Decagonal Symmetry,” Sci. Rep. 5, 9111 (2015).