Photon Qubit is Made of Two Colors

Philipp Treutlein

Viewpoint

Photon Qubit is Made of Two Colors

Department of Physics, University of Basel, Klingelbergstrasse 82, CH-4056 Basel, Switzerland

November 23, 2016• Physics 9, 135

Single particles of light can be prepared in a quantum superposition of two different colors, an achievement that could prove useful for quantum information processing.

Figure caption — **Figure 1:** The illustration shows the conversion of a photon of one frequency, or color, into a photon that is in a superposition of two colors, and the subsequent verification of the photon’s coherence with Ramsey spectroscopy. (Bottom) A single photon of frequency $𝜈_{A}$ (red) is sent through a nonlinear optical fiber, converting it to a superposition of $𝜈_{A}$ and another frequency $𝜈_{B}$ (blue). An adjustable delay changes the relative phase of the two frequency components in the superposition before they are mixed again. The resulting state is analyzed by separating the two frequency components in a demultiplexer and detecting the single photon, thereby projecting it onto one of its two colors. (Top) A vector on the Bloch sphere with polar angle $𝜃$ and azimuthal angle $𝜑$ represents the state of the photon through the various steps of the conversion.

The discovery of the photon, the quantum particle of light, played a key role in the development of quantum physics. Today, photons are among the most advanced building blocks for quantum technologies, such as quantum computing [1], secure communication [2], and precision measurement [3]. These applications typically rely on quantum control of a photon’s polarization or its spatial mode. Surprisingly, the most manifest property of light—its color or frequency—is difficult to manipulate on the quantum level. An experiment now demonstrates a toolbox for creating, manipulating, and detecting single photons in a quantum superposition of two discrete frequencies [4]. The approach requires an interaction between different frequency components of light, which Stéphane Clemmen from Cornell University, New York, and colleagues have achieved by making use of nonlinear processes in optical fibers. Such photonic quantum bits (qubits) could be useful for connecting quantum systems operating at different frequencies in a quantum network.

According to quantum physics, monochromatic light of frequency $𝜈$ , such as the light emitted by a laser, is composed of photons of energy $E = h 𝜈$ , where $h$ is the Planck constant. Polychromatic light, such as the light emitted by the Sun, contains photons of many different frequencies. However, each individual photon usually has a well-defined frequency and energy. Interestingly, the superposition principle of quantum physics allows for yet another version of polychromatic light: a single photon in a superposition of two discrete frequencies $𝜈_{A}$ and $𝜈_{B}$ . In this case, neither the frequency nor the energy of the photon is well defined. In some sense, such a “bichromatic” photon can be thought of as having two different colors at the same time, only one of which would be revealed if the photon were measured by a spectrometer or detected by eye.

However, the creation and manipulation of bichromatic photons turns out to be challenging. The difficulty is that such processes require an interaction between photons of different frequencies, and in most media, light beams do not interact. The situation changes if light propagates in a nonlinear medium, where the optical properties vary with the intensity of light. The nonlinear response results in an interaction between photons, providing a means with which to convert them to a different frequency. To make this process efficient, however, the medium must be pumped with separate high-power laser beams. These beams are tuned to a different frequency than the weak single-photon signal, but care must be taken to avoid noise processes that generate additional photons in the signal channel. Several experiments have succeeded in creating suitable single-photon nonlinearities. Clemmen et al. build on this work by not only creating bichromatic photons, but also by manipulating them and demonstrating their coherence.

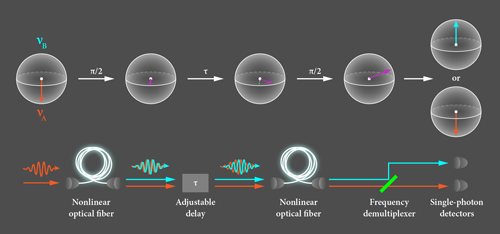
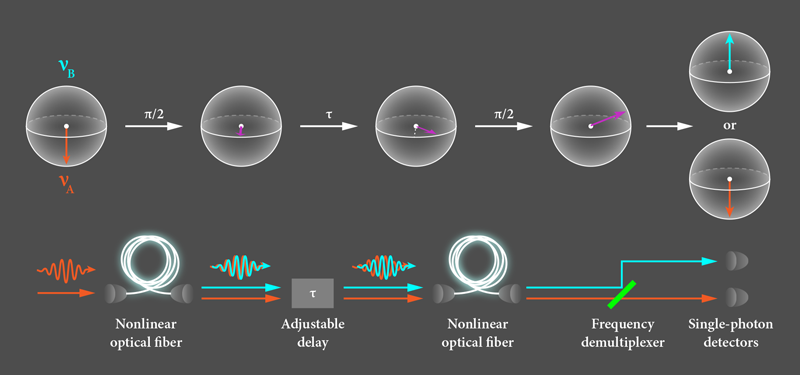
In their experiments, Clemmen et al. realize the efficient frequency conversion of single photons with a process called Bragg-scattering four-wave mixing. The main ingredient in this approach is a 100-m-long fiber, which the authors pump with two laser beams of unequal frequencies to obtain the required nonlinear response. The frequency difference between the beams determines the difference between the frequencies $𝜈_{A}$ and $𝜈_{B}$ involved in the final single-photon superposition. The team achieves the necessary low noise level by cooling the fiber in a cryostat. Within this setup, sending a single photon of frequency $𝜈_{A}$ and quantum state $| 𝜈_{A} 〉$ through the fiber converts the photon state into a superposition, $| Ψ 〉 = sin (𝜃 ∕ 2) e^{i 𝜑} | 𝜈_{A} 〉 + cos (𝜃 ∕ 2) | 𝜈_{B} 〉$ , where $𝜃$ is the mixing angle and $𝜑$ is the relative phase between the frequency components. The angles $𝜃$ and $𝜑$ can be adjusted by tuning the amplitude and phase of the pump lasers, allowing the researchers to encode one bit of quantum information on the photon (see representation at the top of Fig. 1).

Importantly, Clemmen et al. prove that they have generated a coherent superposition $| Ψ 〉$ rather than an incoherent mixture in which photons randomly acquire one of the two frequencies. To do so, the researchers perform Ramsey spectroscopy, a technique commonly used to measure coherence in atomic clocks or nuclear magnetic resonance (NMR). The Ramsey sequence is illustrated in Fig. 1. The researchers adjust the pump lasers such that after the photon passes through the fiber it is in an equal superposition of the two photon frequencies, or $| Ψ 〉 = (e^{i 𝜑} | 𝜈_{A} 〉 + | 𝜈_{B} 〉) ∕ \sqrt{2}$ . In the terminology of NMR, this corresponds to a $𝜋 ∕ 2$ pulse. Subsequently, they adjust the phase, $𝜑$ , by introducing a propagation delay. Finally, they send the photon through the fiber a second time, corresponding to a second $𝜋 ∕ 2$ pulse, which converts the state to $| Ψ 〉 = i sin (𝜑 ∕ 2) | 𝜈_{A} 〉 + cos (𝜑 ∕ 2) | 𝜈_{B} 〉$ . To analyze the state, they separate the two frequency components and detect each with a single-photon detector. When they vary the propagation delay, and therefore $𝜑$ , the probability of detecting the photon oscillates sinusoidally between the two detectors, as expected. The observed contrast of these “Ramsey fringes” reaches up to 65%, proof that a coherent superposition is being generated. Moreover, the researchers show that there is only a small probability of detecting more than one photon at a time, confirming that their superposition state preserves the single-photon character of the initial state.

It is very appealing to see that a single particle of light can be in a superposition of two different colors. So far, the wavelengths involved are in the infrared near 1280 nm—outside the range of human vision—and differ by about 4 nm. But when translated to the visible spectrum (roughly 380–780 nm), such a wavelength difference could be discriminated with the bare eye. In the future, the methods that Clemmen et al. have demonstrated could be used to interface quantum systems operating at different frequencies, such as solid-state and atomic quantum memories [5–8]. One could envision two physically different quantum memories, each absorbing one part of the single photon in a frequency superposition. This would entangle the quantum memories because they share a single excitation in a coherent way. Such a protocol may be useful for creating quantum networks [9, 10], which could be the basis for quantum communication, computing, and simulation. Another application of the bichromatic qubits could be spectroscopy that requires only small amounts of light: the idea would be to look for spectrally dependent phase changes in the qubits’ states. These applications would benefit from extending the technique demonstrated by Clemmen et al. to larger frequency or wavelength differences.

References

P. Kok, W. J. Munro, K. Nemoto, T. C. Ralph, J. P. Dowling, and G. J. Milburn, “Linear Optical Quantum Computing with Photonic Qubits,” Rev. Mod. Phys. 79, 135 (2007).
N. Gisin and R. Thew, “Quantum Communication,” Nature Photon. 1, 165 (2007).
J. Aasi et al. (The LIGO Scientific Collaboration), “Enhanced sensitivity of the LIGO Gravitational Wave Detector by Using Squeezed States of Light,” Nature Photon. 7, 613 (2013).
S. Clemmen, A. Farsi, S. Ramelow, and A. Gaeta, “Ramsey Interference with Single Photons,” Phys. Rev. Let. 117, 223601 (2016).
I. Usmani, C. Clausen, F. Bussières, N. Sangouard, M. Afzelius, and N. Gisin, “Heralded Quantum Entanglement Between Two Crystals,” Nature Photon. 6, 234 (2012).
A. G. Radnaev, Y. O. Dudin, R. Zhao, H. H. Jen, S. D. Jenkins, A. Kuzmich, and T. A. B. Kennedy, “A Quantum Memory with Telecom-Wavelength Conversion,” Nature Phys. 6, 894 (2010).
M. T. Rakher, L. Ma, M. Davanço, O. Slattery, X. Tang, and K. Srinivasan, “Simultaneous Wavelength Translation and Amplitude Modulation of Single Photons from a Quantum Dot,” Phys. Rev. Lett. 107, 083602 (2011).
J.-P. Jahn, M. Munsch, M. Davanço, O. Slattery, X. Tang, and K. Srinivasan, “An Artificial Rb Atom in a Semiconductor with Lifetime-Limited Linewidth,” Phys. Rev. B 92, 083602 (2015).
H. J. Kimble, “The Quantum Internet,” Nature 453, 1023 (2008).
N. Sangouard, C. Simon, H. de Riedmatten, and N. Gisin, “Quantum Repeaters Based on Atomic Ensembles and Linear Optics,” Rev. Mod. Phys. 83, 33 (2011).

About the Author

Philipp Treutlein is an Associate Professor of Physics at the University of Basel in Switzerland. He studied physics at the University of Konstanz, Germany, and at Stanford University, US, where he was a Fulbright fellow in Steven Chu's lab. Philipp obtained his Ph.D. in 2008 from the Ludwig-Maximilians University of Munich, where he worked in the group of Theodor Hänsch on experiments with ultracold atoms on atom chips. In 2010 Philipp started his own group at the University of Basel, working on quantum metrology with ultracold atoms and exploring quantum interfaces of atoms and solid-state systems.