Matter-Light Condensates Reach Thermal Equilibrium
In a laser, coherent light is created by stimulated emission of photons from an “inverted” state of matter that is significantly out of thermal equilibrium. “Inverted” means that excited states of the matter are more occupied than lower energy states, so that emission is more likely than absorption. The coherence of laser light is closely related [1] to a quite different, and less commonly encountered, state of matter—a Bose-Einstein condensate (BEC). In the textbook description of a BEC, at low enough temperatures or high enough densities, a large number of particles occupy the same state, producing a coherent state of matter. In contrast to laser light, the textbook BEC is in thermal equilibrium. Condensates of polaritons—half-light, half-matter quasiparticles—have so far been found in conditions halfway between those of an equilibrium BEC and those of a laser. Work by Yongbao Sun, from the Massachusetts Institute of Technology, Cambridge, and colleagues [2] now shows that such polariton condensates can be tuned to reach a thermal equilibrium state. With this tunability between an equilibrium and nonequilibrium state, researchers can explore how the character of phase transitions evolves between the two limits.
The differences between a laser, a BEC, and a polariton condensate are rooted in what determines how particles occupy states (or modes) in each system. In a typical laser, the occupations are set by stimulated emission. That is, the rate at which photons are emitted into a given mode increases with the number of photons already in that mode. This is also true for a polariton condensate. However, what matters in this case is not emission into a mode but scattering between modes: the existing population of particles in a given mode stimulates further scattering into that mode. When such scattering rates compete with particle losses, the balance between the two processes sets the population of each mode, resulting in a nonequilibrium distribution. In contrast, for a system in thermal equilibrium, the populations of each mode follow a universal law, with the population dependent only on the energy of a mode. For identical bosons, this law is known as the Bose-Einstein distribution. For polaritons, when loss rates are small enough, that is, when polariton lifetimes are long, the Bose-Einstein distribution is recovered. This recovery of thermal equilibrium in the limit of long lifetime should not be surprising. Statistical physics is based on the idea that everything that can happen does happen, with a probability determined only by the energy of the state, so that one can use these universal laws rather than following the dynamics of individual particles.
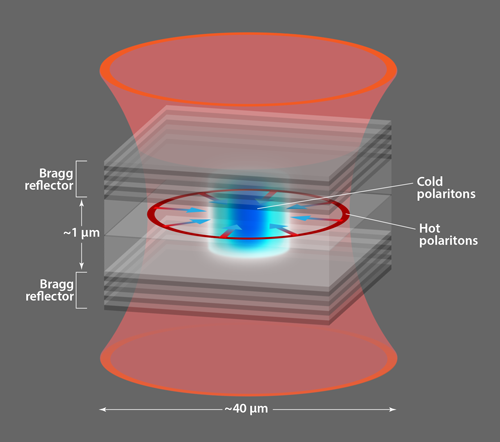
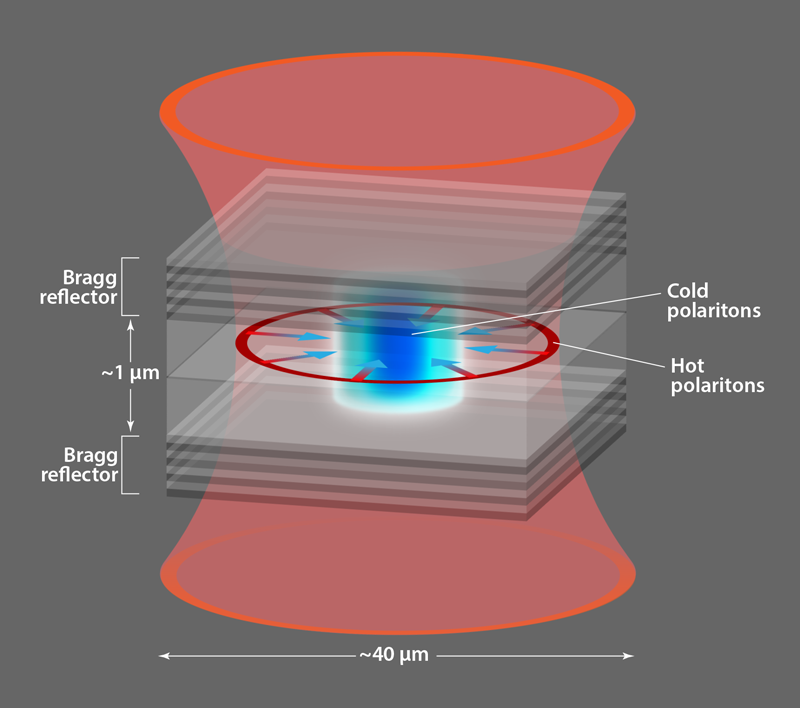
Polariton condensates form an ideal system to study the emergence of thermal equilibrium. A polariton is a superposition of a photon in an optical microcavity and an exciton (an electron-hole pair) in a semiconductor structure, which is embedded in the microcavity (Fig. 1). Polaritons inherit properties from both their constituents. From the matter component, the exciton, they acquire interactions several orders of magnitude greater than those found in typical optical materials; from the light component, the photon, they acquire a small effective mass and a finite lifetime. Because of the two-dimensional confinement of both components, polaritons are also two-dimensional. So far, experiments on polaritons have produced condensates in nonequilibrium conditions [1, 3]. This is not necessarily a drawback, as new physical phenomena originate from the nonequilibrium character of such condensates (for recent examples, see Ref. [1]). The new results by Sun and co-workers show that the same system can be tuned from a highly nonequilibrium state all the way to an equilibrium state by extending the lifetime of the polaritons.
Reaching an equilibrium state relies on boosting the lifetime of the polaritons, which requires improvement in the quality of the mirrors that form the microcavity. The breakthrough underpinning this experiment comes from the exceptionally high quality of the mirrors. Sun and co-workers used a kind of mirror called a distributed Bragg reflector: alternating semiconducting layers with different dielectric constants (Fig. 1). At each layer interface, there is partial reflection and partial transmission of light. The reflections can be made to add constructively, so that the more layers the mirrors have, the greater the reflection (and the smaller the transmission) and thus the greater the lifetime of polaritons inside the microcavity. The mirrors employed by Sun and colleagues (grown by co-authors Loren Pfeiffer and Ken West from Princeton University) provide lifetimes 10 times longer than those previously available. As is often the case, apparently incremental progress in device fabrication and material quality leads to a transformative effect on the basic science that can be accessed.
Despite their enhanced lifetime, polaritons can escape from the cavity, so an external “pump” laser is required to compensate for this loss. The external pump creates a population of hot polaritons, which then scatter into the polariton condensate. These hot polaritons do not live long enough to reach thermal equilibrium, and in all previous experiments, they coexisted with the polariton condensate. However, for long-lifetime samples, polaritons are able to move large distances (up to millimeters) before they decay. This can allow researchers to spatially separate the hot polaritons and the condensate. Sun and colleagues used a ring-shaped pump laser beam that produces a ring of hot polaritons. This ring serves two purposes: it feeds a cold cloud of polaritons in the middle of the ring by scattering from the hot polaritons; and it traps the cloud by repulsion from the same polaritons (Fig. 1). Similar methods have enabled the design and engineering of arbitrarily shaped traps [4].
Sun and colleagues’ results appear to match well with the “textbook” theory of a Bose-Einstein condensate of noninteracting bosons. However, this is somewhat surprising, as polaritons do interact. Indeed, in the absence of interactions, particles cannot scatter, and so do not reach thermal equilibrium. Moreover, in a two-dimensional system, which is the case here, thermal fluctuations of the condensate mean there is actually no true long-range order but, instead, the exotic state of matter for which Michael Kosterlitz and David Thouless were, in part, awarded the 2016 Nobel Prize in Physics. In a trapped cloud of particles, there is a crossover between a “true” BEC for weak interactions and this exotic state at larger interaction strengths [5]. Given that Sun and co-workers have elsewhere [6] reported that polaritons show energy shifts due to interactions that are stronger than had been anticipated [1], an intriguing direction for future work is to see whether this expected crossover arises. If it doesn’t, then physicists will have to figure out why polaritons can show large energy shifts, yet behave as if they are noninteracting in terms of their mode populations. The nature of this crossover is potentially even more complicated for particles with finite lifetimes [7], so the ability to study this crossover in samples with long lifetimes [2, 8] may allow these complex questions to be answered.
Improving material properties are currently driving many exciting investigations in polariton physics. In well-studied materials such as gallium arsenide, the material used here, one could explore whether the enhanced lifetimes allow the demonstration and study of strongly correlated states of polaritons [1, 9]. Additionally, a host of new materials exists that may display quantum behavior at high temperatures, such as transition-metal dichalcogenides, organic materials, or wide-band-gap semiconductors [10].
This research is published in Physical Review Letters.
References
- I. Carusotto and C. Ciuti, “Quantum Fluids of Light,” Rev. Mod. Phys. 85, 299 (2013).
- Y. Sun, P. Wen, Y. Yoon, G. Liu, M. Steger, Loren N. Pfeiffer, K. West, D. W. Snoke, and K. A. Nelson, “Bose-Einstein Condensation of Long-Lifetime Polaritons in Thermal Equilibrium,” Phys. Rev. Lett. 118, 016602 (2017).
- J. Kasprzak et al., “Bose–Einstein Condensation of Exciton Polaritons,” Nature 443, 409 (2006).
- G. Tosi, G. Christmann, N. G. Berloff, P. Tsotsis, T. Gao, Z. Hatzopoulos, P. G. Savvidis, and J. J. Baumberg, “Sculpting Oscillators with Light Within a Nonlinear Quantum Fluid,” Nature Phys. 8, 190 (2012).
- R. J. Fletcher, M. Robert-de-Saint-Vincent, J. Man, N. Navon, R. P. Smith, K. G. H. Viebahn, and Z. Hadzibabic, “Connecting Berezinskii-Kosterlitz-Thouless and BEC Phase Transitions by Tuning Interactions in a Trapped Gas,” Phys. Rev. Lett. 114, 255302 (2015).
- Y. Sun, Y. Yoon, M. Steger, G. Liu, L. N. Pfeiffer, K. West, D. W. Snoke, and K. A. Nelson, “Polaritons Are Not Weakly Interacting: Direct Measurement of the Polariton-Polariton Interaction Strength,” arXiv:1508.06698.
- J. Keeling, L. M. Sieberer, E. Altman, L. Chen, S. Diehl, and J. Tonerin, in Universal Themes of Bose-Einstein Condensation, edited by D. Snoke, N. Proukakis, and P. Littlewood (Cambridge University Press, Cambridge, to be published), Chap. 11; arXiv:1610.05737.
- D. Caputo et al., Topological Order and Equilibrium in a Condensate of Exciton-Polaritons, arXiv:1610.05737.
- M. J. Hartmann, “Quantum Simulation with Interacting Photons,” J. Opt. 18, 104005 (2016).
- D. Sanvitto and S. Kéna-Cohen, “The Road Towards Polaritonic Devices,” Nature Mater. 15, 1061 (2016).