Storing Light in the Dark
Among the many rebellious processes in nature, the spontaneous emission of photons from atoms and molecules is particularly hard to control. True to its name, the process occurs at random points in time, and it can be deleterious to experiments involving atoms in carefully prepared excited states, such as those used in the storage of quantum information. A new way to slow down the spontaneous emission rate of atoms in a cloud has now been demonstrated by William Guerin from the University of Nice Sophia-Antipolis, France, and his co-workers. They were able to increase the lifetime of the excited state of an atom by as much as a factor of 300 [1]. Importantly, the suppressed spontaneous emission serves as evidence that the researchers were able to successfully prepare a large number of atoms in a so-called subradiant state. Prior to this work, such states have only been observed indirectly [2] or for the special case of two emitting dipoles [3, 4]. Guerin et al. have therefore achieved the first experimental observation of subradiance of many emitters (N≫2).
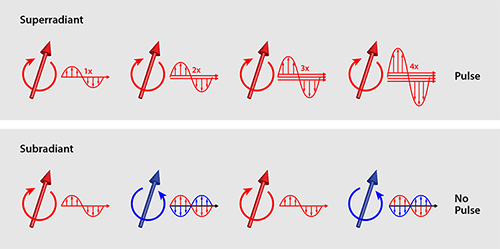
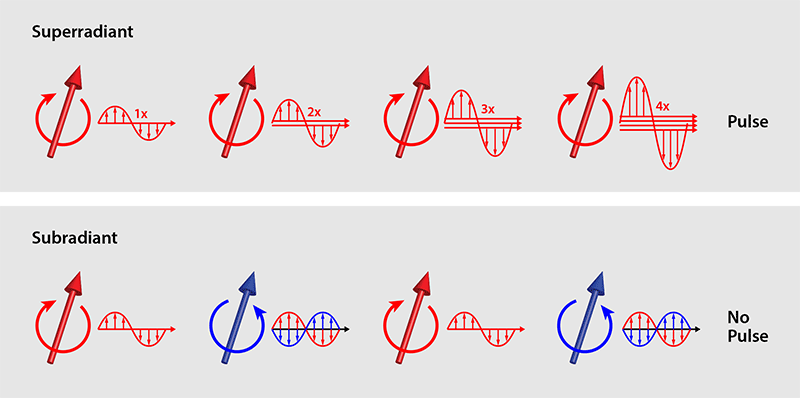
In 1954, Robert Dicke wrote a paper predicting that cooperative effects in an ensemble of identical atoms could either enhance spontaneous emission (superradiance) or suppress it (subradiance) [5]. The effects have both a quantum and a classical side to them. They are initiated by the spontaneous emission of excited atoms, which results from quantum fluctuations in the vacuum. This emission then evolves into a classical interference process in which the interaction between the electric dipoles of the atoms causes them to spontaneously lock together, leading to synchronized emission. This lock-in phenomenon depends on the atom dipoles being indistinguishable for the emitted electromagnetic wave; that is, the excited states of the atoms must have identical transition frequencies, and their dipoles must all point in the same direction. In this case, the electromagnetic field only depends on the sum of the dipoles and not the individual ones.
Superradiance occurs if all individual dipoles contribute positively to the collective dipole (Fig. 1, top panel). As Dicke showed, this effect can be traced back to the collective formation of so-called symmetric states, such that there is constructive interference between the atom emissions. When this happens, spontaneous emission is greatly accelerated and the atoms can emit an intense pulse that is strongly directional in space and time.
In contrast, subradiance occurs when the dipoles are in antisymmetric states, meaning their phases are locked but have opposite signs (Fig. 1, bottom). In this case, the collective dipole is smaller than any individual dipole, and the emission process slows down tremendously—to the point that the dipoles can become completely decoupled from fluctuations in the vacuum.
Although subradiance and superradiance stem from the same underlying phase-lock mechanism, subradiance is much more difficult to observe. While superradiant emission produces a very intense, directional burst of photons, subradiant emission is smeared out in space and time and is therefore harder to detect. Also, because superradiant emission occurs so rapidly, it is relatively insensitive to effects that disrupt the indistinguishability of the atoms, such as Doppler shifts, Lamb shifts, atomic motion, and perturbations to the atomic energy levels from the light’s electric field (ac Stark shift). Even in hot atomic vapors, where the atoms move at high speeds relative to each other, superradiant emission is like a “flash” that freezes this motion [6]. The subradiant state, however, is relatively long lived compared to atomic motion. The atoms can therefore be distinguished by their relative speeds, which is why subradiance has never been observed in hot atomic vapor. Moreover, the long observation time needed to see a subradiant state leaves it susceptible to the effects of van der Waals dephasing, which breaks the symmetry of the dipolar interactions. As a result of these many detection hurdles, the ability to see N-body subradiance has long been in doubt [7].
Guerin et al. circumvent these difficulties by focusing on a large cloud of cold atoms in which the interatomic distances are much greater than the wavelength of the emitted light—the so-called weakly excited extended-sample limit. In such a low-density gas, many of the near-field effects that are disruptive to subradiance are negligible, but the long-range interaction between the dipoles is still strong enough to allow for the creation of stable antisymmetric states. Furthermore, in the weak-excitation limit, the phases of the antisymmetric states are immune to the ac Stark shift. The authors outlined the theoretical basis for this experiment in 2012 [7]. Now, they have written their own success story by demonstrating the suppression of spontaneous emission by many orders of magnitude, in agreement with their theory.
In their experiment, they loaded a gas of roughly one billion cold rubidium (Rb) atoms into a magneto-optical trap, with which they could control the gas size, density, and temperature. To excite the atoms, they illuminated the cold-atom sample with a series of laser pulses, and after each pulse they collected the (spontaneous) fluorescent emission from the atoms with a photomultiplier. Most of this emission occurred quickly, but a small percentage of it was emitted over a time scale that was 300 times longer than the natural lifetime of the Rb atom excitation—strong evidence that the gas cloud was in a subradiant state. This alone is remarkable, as it demonstrates subradiance is possible without the microscopic control of the positions, distances, and dipole orientations that were assumed necessary to see the effect.
The work by Guerin et al. paves the way to applications that use carefully timed excitations of Dicke states. The antisymmetric, or “dark,” states that form in subradiant systems can store photons—and the information encrypted onto them—for a long time. These states can therefore be the backbone for new types of quantum memories [8]. For example, a recent proposal [9] outlines a protocol for switching between subradiant and superradiant states, where the former would be used to store information for a long time and the latter would be used for fast readouts. Furthermore, the ability to inhibit spontaneous decay could trigger new designs in the fabrication of solar cells, where spontaneous emission is one of the key limits to higher efficiencies. In addition, the cold-atom gas described by Guerin et al. provides a versatile platform for studying weakly excited symmetry-protected many body states. Such states are found in magnetic systems (specifically, spin chains) and systems with disorder [10, 11], indicating that interest in subradiance extends well beyond cold-atom physics [1, 4, 9].
This research is published in Physical Review Letters.
References
- W. Guerin, M. O. Araujo, and R. Kaiser, “Subradiance in a Large Cloud of Cold Atoms,” Phys. Rev. Lett. 116, 083601 (2016).
- D. Pavolini, A. Crubellier, P. Pillet, L. Cabaret, and S. Liberman, “Experimental Evidence for Subradiance,” Phys. Rev. Lett. 54, 1917 (1985).
- R. G. DeVoe and R. G. Brewer, “Observation of Superradiant and Subradiant Spontaneous Emission of Two Trapped Ions,” Phys. Rev. Lett. 76, 2049 (1996).
- B. H. McGuyer, M. McDonald, G. Z. Iwata, M. G. Tarallo, W. Skomorowski, R. Moszynski, and T. Zelevinsky, “Precise Study of Asymptotic Physics with Subradiant Ultracold Molecules,” Nature Phys. 11, 32 (2014).
- R. H. Dicke, “Coherence in Spontaneous Radiation Processes,” Phys. Rev. 93, 99 (1954).
- M. Gross, J. M. Raimond, and S. Haroche, “Doppler Beats in Superradiance,” Phys. Rev. Lett. 40, 1711 (1978).
- T. Bienaimé, N. Piovella, and R. Kaiser, “Controlled Dicke Subradiance from a Large Cloud of Two-Level Systems,” Phys. Rev. Lett. 108, 123602 (2012).
- L.M. Duan, M. D. Lukin, J. I. Cirac, and P. Zoller, “Long-Distance Quantum Communication with Atomic Ensembles and Linear Optics,” Nature 414, 413 (2001).
- M. O. Scully, “Single Photon Subradiance: Quantum Control of Spontaneous Emission and Ultrafast Readout,” Phys. Rev. Lett. 115, 243602 (2015).
- A. Carmele, M. Heyl, C. Kraus, and M. Dalmonte, “Stretched Exponential Decay of Majorana Edge Modes in Many-Body Localized Kitaev Chains under Dissipation,” Phys. Rev. B 92, 195107 (2015).
- D. Plankensteiner, L. Ostermann, H. Ritsch, and C. Genes, “Selective Protected State Preparation of Coupled Dissipative Quantum Emitters,” Sci. Rep. 5, 16231 (2015).