Rethinking Superhydrophobicity
Surface roughness and chemical heterogeneities can change the wetting properties of solids [1]. For example, adding surface topography at the micrometer scale onto a water-repellent (hydrophobic) material produces superhydrophobicity, as observed on a lotus leaf or on so-called “self-cleaning” materials [2]. For such a surface, a water drop rests on a composite layer made of air and solid, allowing it to adopt a nearly spherical shape (in contrast with the more hemispherical shape on hydrophobic surfaces). If the surface is tilted, the drop rolls off easily. Researchers characterize superhydrophobicity by measuring the contact angles that a water drop makes with the surface right before rolling, both at the front (advancing) edge and back (receding) edge of the liquid-solid interface (see Fig. 1). However, there is evidence that large contact angles are sometimes underestimated by common measurement techniques that use unmagnified (macroscopic) imaging. Frank Schellenberger and his colleagues from the Max Planck Institute for Polymer Research in Germany have performed the first microscopic imaging of how a contact line advances on a rough superhydrophobic surface [3]. The team found that commonly used definitions of superhydrophobicity based on the advancing contact angle are unreliable. Instead, they propose using the receding contact angle, which gives consistent values between macroscopic and microscopic techniques. This redefinition could be embraced by designers looking for more efficient superhydrophobic materials.
The contact angle for ideal surfaces—those that are smooth and chemically homogeneous—can be found by balancing the surface forces at the contact line where the solid, liquid, and gas phases meet. The result is the familiar Young’s angle. However, most surfaces that we experience in our everyday life are not ideal. As shown in investigations over the last 50 years [4], the measured static angle that a liquid drop makes with a rough surface can be both larger and smaller than Young’s angle. The advancing contact angle is the maximum angle that a drop can make on a given surface, whereas the receding contact angle is the minimum.
Superhydrophobic surfaces and super-liquid-repellent surfaces more generally have been studied extensively in recent years as they offer new possibilities for both academic and industrial research. Such surfaces are involved in a wide variety of applications that include the design of self-cleaning surfaces [2] and the quest for more efficient fog collection systems meant to supply fresh water in arid environments [5]. In the literature, a solid is typically deemed superhydrophobic when the apparent advancing contact angle with water is greater than 150° and the contact angle hysteresis (the difference between the advancing and receding contact angles) is less than 10°. These angles are “apparent” because they are determined on a macroscopic scale with angle-measuring goniometers, video cameras, and drop-shape analyses. But these low-resolution measurements are difficult for contact angles greater than about 150°, in which case the drop’s underside is nearly parallel with the surface, making it hard to determine the exact point where the water and solid meet.
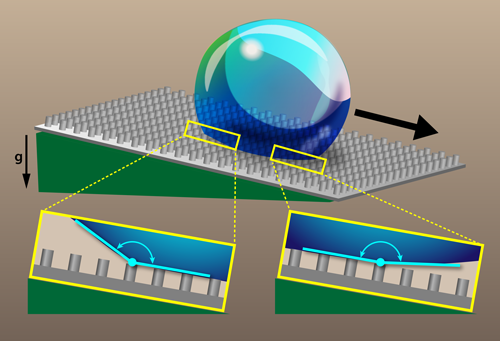
To obtain a clearer picture of the wetting behavior on superhydrophobic surfaces, Schellenberger et al. microscopically filmed the motion of contact lines [3]. The team fabricated microtextured surfaces with an epoxy-based photoresist. The surface textures consisted of cylindrical posts arranged on a square lattice. The size and separation of the posts were varied, with post diameters in the 5–25 𝜇m range, post heights in the 9–16 𝜇m range, and lattice spacings in the 10–75 𝜇m range. Each sample was then coated with hydrophobic silane molecules to produce a superhydrophobic surface. The team deposited a microliter-sized water drop onto a surface tilted at the roll-off angle (around 9°), which is the smallest angle needed to get the drop to roll. The drop remained stationary for about 30 s before rolling down the surface. However, during this prerolling “induction time,” the drop’s edge along the surface did move. Using laser scanning confocal microscopy, the researchers captured images with submicrometer resolution, showing the temporal evolution of the moving contact lines on both the advancing side and receding side of the drops.
Schellenberger et al. observed distinct behavior at the advancing and rear side of their drops. On the rear side, the motion was discontinuous. For several seconds, the receding edge of the drop was pinned on top of a post, while the contact angle there steadily decreased. When the angle reached a critical value, the receding edge jumped to the next post. The team found that this critical angle matched the apparent receding contact angle measured macroscopically with a goniometer. The advancing side of the drop, on the other hand, was observed to move continuously, with the contact angle on the advancing front being larger than that observed with macroscopic measurements. In fact, the team found that the advancing contact angle reached values as high as 180°, confirming earlier theoretical predictions [6–8]. Because of the discrepancies in the micro- and macroscopic advancing contact-angle measurements, the authors propose a new definition for superhydrophobicity that instead uses the apparent receding contact angle. They imagine the community would decide a value (e.g., 150°), and all materials with an apparent receding contact angle greater than that would be deemed superhydrophobic. Besides being more consistent with microscopic observations, this redefinition of superhydrophobicity has the advantage that the apparent receding angle doesn’t depend on the drop size, like some other proposed definitions based on roll-off angle.
The work of Schellenberger et al. could have several consequences for the physics of wetting. First, it could simplify the determination of the roll-off angle, which is typically estimated using both the advancing and receding contact angles. The authors argue that the advancing contact angle is 180° “for many if not all superhydrophobic surfaces,” so the roll-off angle will, in general, only depend on the receding contact angle. Second, the authors argue that a commonly used equation, called the Cassie-Baxter equation [9], does not accurately describe the apparent advancing contact angle for drops that rest on top of the protrusions of a superhydrophobic surface.
This work might also play a role in the search for new superhydrophobic systems. Researchers typically alter the shape, size, and position of the protrusions on the surfaces of test materials to see what effect this has on the wetting behavior. With this new definition of superhydrophobicity, these design efforts could become more efficient at discovering materials that optimize desired properties. In any case, this work underlines that it is sometimes important to think about well-studied problems in a different way.
This research is published in Physical Review Letters.
References
- P. G. de Gennes, F. Brochard-Wyart, and D. Quéré, “Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves,” (Springer, New York, 2004)[Amazon][WorldCat].
- W. Barthlott and C. Neinhuis, “Purity of the Sacred Lotus, or Escape from Contamination in Biological Surfaces,” Planta 202, 1 (1997).
- F. Schellenberger, N. Encinas, D. Vollmer, and H.-J. Butt, “How Water Advances on Superhydrophobic Surfaces,” Phys. Rev. Lett. 116, 096101 (2016).
- R. E. Johnson, and R. H. Dettre, “Contact Angle Hysteresis. I. Study of an Idealized Rough Surface,” Adv. Chem. Ser. 43, 112 (1964); R. H. Dettre and R. E. Johnson, “Contact Angle Hysteresis. II. Contact Angle Measurements on Rough Surfaces,” 43, 136 (1964).
- K. C. Park, S. S. Chhatre, S. Srinivasan, R. E. Cohen, and G. H. McKinley, “Optimal Design of Permeable Fiber Network Structures for Fog Harvesting,” Langmuir 29, 13269 (2013).
- L. Gao and T. J. McCarthy, “The “Lotus Effect” Explained: Two Reasons Why Two Length Scales of Topography Are Important,” Langmuir 22, 2966 (2006).
- F. E. Bartell and J. W. Shepard, “Surface Roughness as Related to Hysteresis of Contact Angles. II. The Systems Paraffin-3 Molar Calcium Chloride Solution–Air and Paraffin–Glycerol–Air,” J. Phys. Chem. 57, 455 (1953).
- C. W. Extrand, “Model for Contact Angles and Hysteresis on Rough and Ultraphobic Surfaces,” Langmuir 18, 7991 (2002).
- A. B. D. Cassie and S. Baxter, “Wettability of Porous Surfaces,” Trans. Faraday Soc. 40, 546 (1944).