Quantum Hoverboards on Superconducting Circuits
Building a quantum computer or quantum simulation device is a multidisciplinary undertaking that has driven a lot of cutting-edge research. But there is still a long way to go before a fully operational quantum machine becomes a reality. The basic recipe for achieving this goal may sound quite simple. First, identify a set of suitable quantum systems that can be well isolated from the environment to protect their “quantumness.” Second, assemble them together in a controlled and scalable way. The problem is, however, that in nature, isolation does not come along easily with control and scalability. Ge Yang from the University of Chicago, Illinois, and his colleagues have demonstrated a device [1] that could potentially lead to robust yet controllable qubit architectures. In the new scheme, electrons floating on top of a superfluid-helium film (which could encode quantum bits) are combined with a high-quality superconducting circuit (which could enable the readout and control of the qubits).
Since atoms and molecules tend to either stick to solid surfaces or sink into a liquid, it might at first seem surprising that electrons could stably float on top of a liquid-helium film. This long-studied phenomenon arises from two competing phenomena [2]. On the one hand, an effect known as Pauli blocking prevents two electrons from occupying the same quantum state. This makes the densely packed fluid of closed-shell helium atoms impenetrable for an additional incoming electron. On the other hand, the electrons are still attracted towards the helium by the “image charge” they induce, similarly to a charge attracted towards a metallic surface. The combination of the two effects results in a potential that traps the electrons and localizes them within a 2D sheet floating at a distance of a few nanometers above the helium film.
The key word here is “above,” meaning that the electrons are well separated from all the “dirt” (crystal impurities, phonons, nuclear spins, and the like) that usually quickly destroys electronic quantum coherence inside a solid. The record-high electron mobilities [3] that have been measured for such electron “hoverboards” are direct evidence of their exceptional degree of isolation. One of the few remaining, yet small, sources of decoherence for the electron motion is the coupling of the electrons to tiny ripples on the helium surface (so-called ripplons) [4]. Theoretical studies suggest that such isolation from the environment would lead to quantum-coherence times of spin-superposition states exceeding hundreds of seconds [5]. Using electrodes, the floating electrons can also be confined horizontally, and at sufficiently high densities they are predicted to self-organize and form a triangular Wigner crystal [6]—a neat way to obtain a whole lattice of single-electron quantum systems.
Such a crystal of electrons on top of superfluid helium might sound like an ideal starting point for building quantum devices. However, a major obstacle is the lack of reliable techniques to detect the quantum state or even the presence of individual electrons. The floating electron gas cannot be easily accessed by direct electrical contacts or by optical means. Over 15 years have passed since the first ideas for exploiting liquid helium electrons in quantum computing were put forward [4, 5], but the experimental progress in this direction has been modest. Now, Yang and his colleagues have successfully demonstrated a new readout technique that allows fast and nondestructive detection of electrons on liquid helium thanks to their effect on a nearby high-quality-factor superconducting circuit. This could be just the missing ingredient needed to drive this field forward.
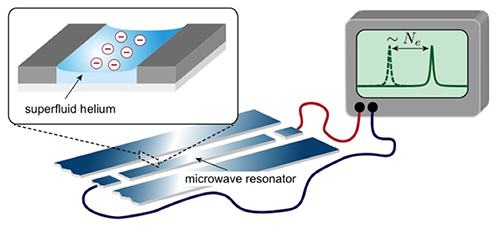
The authors confined the helium film and the surface electrons within a narrow gap between the ground and the center electrodes of a planar superconducting microwave resonator (see Fig. 1). Being superconducting, the resonator (which can be thought of as a centimeter-long planar version of a coaxial cable) can exhibit sharp electromagnetic resonances at GHz frequencies. These resonances depend very sensitively on the dielectric properties of the surrounding environment. Therefore, tiny changes in the electron configuration—in principle, as small as the addition or loss of a single electron—can be monitored in situ and nondestructively by looking at the drift of the resonance frequency. Over the past years, similar readout schemes have found widespread use for quantum state detection in superconducting quantum computation architectures [7].
Yang et al. have successfully applied such ideas to electrons on liquid helium by trapping the floating electrons in the vicinity of such a circuit, where their coupling to the electric field around the resonator is strongest. First, they used the readout technique to measure and adjust the thickness of the helium film with subnanometer resolution—an important parameter defining the trapping conditions. They then sprayed a bunch of electrons emitted from a tungsten filament onto the helium surface, generating a big jump in the circuit’s resonance frequency as these electrons got trapped. Finally, by expelling the electrons a fraction at a time with a negative voltage, they were able to determine the relationship between the number of trapped electrons and the shift of the resonance. A key figure of merit extracted from those measurements (performed with thousands of electrons) is the coupling strength per electron, which quantifies the maximal resonance shift that can be induced by the addition of one electron. Such coupling strength was found to exceed the linewidth of the resonance. This means that in a setup with smaller traps containing only a few electrons [8], the measurement resolution would be sufficient not only to count individual electrons but also to detect in which quantized vibrational state they are in.
What’s next? To realize the full potential of the new scheme, researchers will now need to bring the hybrid systems into a regime in which the electron trapping frequency matches the circuit’s resonance [9]. Under such conditions, a quantum superposition of two microwave photons can be converted into a quantum superposition of two vibrational states, and vice versa. The microwave resonator could then serve as a quantum “bus” that mediates interactions between distant electrons or interfaces the electrons with other quantum systems, like superconducting qubits. Beyond quantum computing applications, such control possibilities may help realize new quantum states of matter in an electron lattice whose constituents can be individually observed and controlled by quantum circuits.
This research is published in Physical Review X.
References
- G. Yang, A. Fragner, G. Koolstra, L. Ocola, D. A. Czaplewski, R. J. Schoelkopf, and D. I. Schuster, “Coupling an Ensemble of Electrons on Superfluid Helium to a Superconducting Circuit,” Phys. Rev. X 6, 011031 (2016).
- M. W. Cole and M. H. Cohen, “Image-Potential-Induced Surface Bands in Insulators,” Phys. Rev. Lett. 23, 1238 (1969).
- K. Shirahama, S. Ito, H. Suto, and K. Kono, “Surface Study of Liquid 3 He Using Surface State Electrons,” J. of Low Temp. Phys. 101, 439 (1995).
- P. M. Platzman and M. I. Dykman, “Quantum Computing with Electrons Floating on Liquid Helium,” Science 284, 1967 (1999).
- S. A. Lyon, “Spin-Based Quantum Computing Using Electrons on Liquid Helium,” Phys. Rev. A 74, 052338 (2006).
- C. C. Grimes and G. Adams, “Evidence for a Liquid-to-Crystal Phase Transition in a Classical, Two-Dimensional Sheet of Electrons,” Phys. Rev. Lett. 42, 795 (1979).
- R. J. Schoelkopf and S. M. Girvin, “Wiring up Quantum Systems,” Nature 451, 664 (2008).
- G. Papageorgiou, P. Glasson, K. Harrabi, V. Antonov, E. Collin, P. Fozooni, P. G. Frayne, M. J. Lea, D. G. Rees, and Y. Mukharsky, “Counting Individual Trapped Electrons on Liquid Helium,” Appl. Phys. Lett. 86, 153106 (2005).
- D. I. Schuster, A. Fragner, M. I. Dykman, S. A. Lyon, and R. J. Schoelkopf, “Proposal for Manipulating and Detecting Spin and Orbital States of Trapped Electrons on Helium Using Cavity Quantum Electrodynamics,” Phys. Rev. Lett. 105, 040503 (2010).