New Crystal Type is Always in Motion
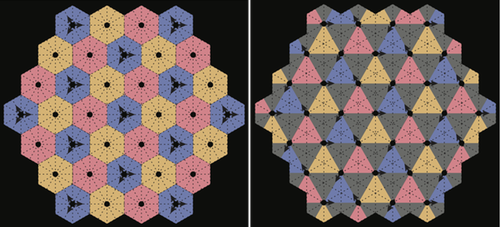
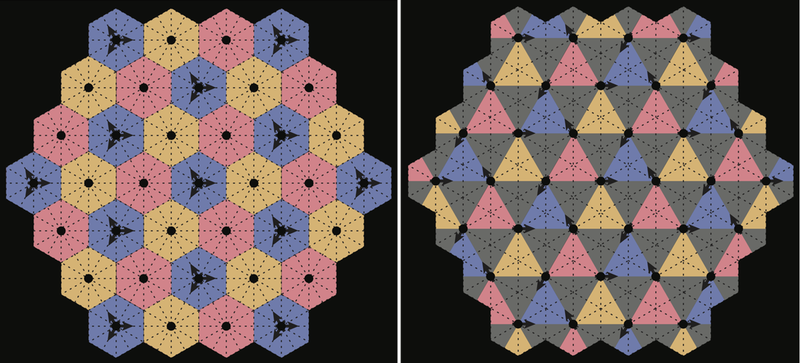
Crystals are usually defined as orderly arrays of static components, such as atoms or molecules. But researchers have now proposed a new kind of crystal in which the order comes instead from the orchestrated movements of the components, such as orbiting satellites. The team calls such systems “choreographic crystals” and developed a formal theory to describe and categorize them.
Latham Boyle of the Perimeter Institute for Theoretical Physics in Waterloo, Canada, says he began thinking about this problem while considering plans for a space observatory for detecting gravitational waves. The proposed observatory would use three sun-orbiting satellites, so they would always be confined to a plane. Boyle realized that four satellites could determine even more about the gravitational wave signal because they need not all lie in a common plane.
Although no one is planning to build such a system, Boyle wondered if the orbits of four satellites could be coordinated in a symmetrical way, so that movies recorded from all of them would look identical. He and his colleagues now describe this four-satellite motion mathematically. Each satellite circles the same central point and orbits parallel to one of the faces of a regular tetrahedron; the relative timing is such that they appear at the corners of a square six times per orbit. This set of orbits “is clearly a very special and beautiful mathematical object, interesting in its own right, like a dynamical analog of the regular tetrahedron,” Boyle says.
The researchers use the theory of symmetry operations to generalize the four-satellite result and examine the orderly configurations available to “swarms” of an arbitrary number of satellites. They define a quantity called the choreography 𝜒 as a measure of the amount of symmetry that can be captured by periodically moving particles. For example, imagine two skaters moving simultaneously north-south and east-west through the center of a square rink and repeatedly reversing course when they reach the edges. The skaters have a higher choreography if they move out of phase—one reaching the edge while the other passes through the center—than if they are in phase, passing through the center at the same instant. In the first case, the moves capture the full symmetry of a square because the same set of rotations and reflections, along with time shifts, will leave the system unchanged. The second case has fewer symmetries. In general, says Boyle, there is a very large number of choreographic crystals, but only a few have very high choreography.
Boyle hopes that choreographic crystals might prove relevant to many mathematical problems, just as the static lattices of standard crystallographic theory have found applications ranging from pure number theory to error correction in computation. The researchers admit that they have no idea if these crystals will exist naturally, although they speculate that the motions of atomic nuclei or electrons in solids might be coordinated this way. If so, it might be possible to detect the choreography using diffraction methods similar to those used in crystallography—the choreography would impart a distinctive signature to the diffraction pattern. Choreographic crystals might alternatively be made artificially, the researchers say, for example by trapping atoms or other small particles in electromagnetic traps created by intense light fields.
The work is “a nice meshing of group theory and periodic dynamics,” says James Crutchfield, a specialist in complex dynamics at the University of California at Davis. He would now like to see a generalization of the approach to less regular “crystals,” such as choreographic quasicrystals, which Boyle and colleagues are already considering.
This research is published in Physical Review Letters.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).