Trampolines Sense a Disturbance in the Force
History has shown that the ability to make better sensors unlocks new experiments in physics. In return, new experiments enable even better sensors. At the intersection of mechanical engineering and quantum physics, researchers are using the tools of nanolithography to engineer sensors based on a new class of mechanical resonators. By fabricating membranes with exquisite mechanical and optical properties, two groups [1, 2] have now demonstrated “trampoline resonators” that may be able to sense extremely weak forces and exhibit quantum motion in a room-temperature environment.
Mechanical systems, in general, are unique in their ability to couple to almost anything. They can be tailored to efficiently measure vastly different phenomena, ranging from microscopic to macroscopic scales. For example, placing a nanomagnet on the end of a micrometer-scale cantilever enables the detection of the force from the spin of a single electron [3]. At the other end of the spectrum, massive suspended mirrors incorporated in kilometer-scale interferometers have recently detected gravitational waves emitted from black holes [4]. Despite the differences in scale and physics, the measurement sensitivity of these technologies hinges on the ability to minimize mechanical dissipation. The dissipation can be thought of as any mechanism through which mechanical energy can be lost. For example, the loss could be through internal friction or by inadvertent radiation of vibrations into the environment. Crucially, and unavoidably, any source of dissipation is also a source of noise. It is this noise that will degrade the performance of a mechanical system as a sensor and obscure any evidence of quantum behavior.
Ideally, the mechanical system would be sufficiently isolated from all noise sources (predominantly thermal noise from the environment) and only coupled to the signals of interest and the readout mechanism. This level of isolation and readout is now readily achieved in atomic systems such as trapped ions [5], where the mechanical resonator is simply the harmonic motion of a single atom held in an electromagnetic trap. Laser light serves as the delicate intermediary between the ion’s motion and the outside world. This connection is what allows the motion to be controlled with optical forces and to be read out with a sensitivity that is only limited by the laws of quantum mechanics. The scientific community has emulated these techniques to control and to sense the motion of much larger systems, where the mechanical resonator is not a single atom but a bulk solid comprised of trillions of atoms. Not surprisingly, the mechanical dissipation is much worse in these macroscopic mechanical systems, as they are not floating in midair like their atomic counterparts but are physically attached to the outside world.
Using optomechanical interactions, a variety of quantum effects have now been observed in macroscopic mechanical systems [6]. Just like in atomic physics, laser-cooling techniques have been used to rid optomechanical devices of all of their thermal noise, leaving the mechanical system in a pure quantum state. To date, however, these experiments have required operation in a cryogenic environment [7, 8]. Silicon nitride membranes under high tensile stress have emerged as a candidate mechanical resonator whose low optical and mechanical loss might allow quantum behavior to be observed at ambient temperatures [9].
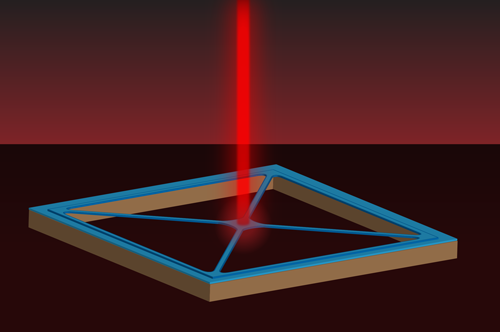
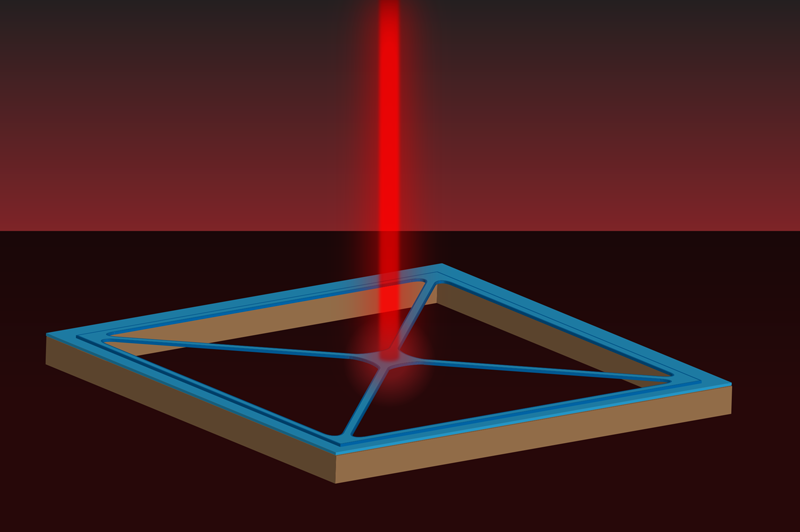
The new experiments from Simon Gröblacher and colleagues at Delft University of Technology, Netherlands [1], and Jack Sankey and co-workers at McGill University, Canada [2], demonstrate the degree to which these membranes can be truly optimized to simultaneously maximize optomechanical interactions while further minimizing both the optical and mechanical losses. Instead of the traditional square membrane anchored around its entire perimeter, the researchers fabricated membranes that are only attached to their silicon frame through narrow tethers (Fig. 1), much like a trampoline suspended from four strings. This geometry is favorable for several reasons. First, the high aspect ratio between the length and thickness of the tethers helps ensure that most of the mechanical energy of the resonator is stored in the tension of the tethers and not in the bending rigidity, which is known to be more lossy. Second, the reduced mass of the entire resonator directly improves the force sensitivity, by ensuring that even the smallest forces will impart relatively large mechanical displacements in the resonator. Last, the trampoline geometry guarantees that there is a fundamental vibration mode whose resonance frequency is well separated from the numerous other (higher-frequency) mechanical resonances that might potentially degrade the performance of the system.
Both experiments [1, 2] clearly showed that the optimized devices can have greatly reduced mechanical dissipation. The researchers verified this by driving the motion of the trampolines at their resonance frequency and measuring how long it took for the systems to lose their mechanical energy. This time scale has improved from seconds to minutes in the authors’ current devices—corresponding to 100 million coherent oscillations of the membrane before the energy is lost. Importantly, the low mechanical dissipation measured in these experiments allows, in principle, for the classical Brownian motion of a trampoline to be brought into a pure quantum state from room temperature using only laser-cooling techniques.
The Delft group demonstrated a method to increase coupling between the light and an ultrathin trampoline. Specifically, the team showed that patterning periodically spaced holes or posts into the center of the membrane can increase its optical reflectivity. This periodic structure forms a two-dimensional photonic crystal, which can enhance the reflectivity without affecting the mechanical properties. Typically, if a trampoline is too thin, it does not interact strongly enough with the laser. Yet the Delft researchers have shown that even trampolines as thin as 20 nm can have the mechanical and optical properties necessary to achieve laser cooling and sensitive readout.
From the low mass and low dissipation of the trampoline resonators, one would expect a very promising force sensitivity. The McGill group directly measured the force sensitivity, demonstrating that they could resolve a 16 attonewton force in one second of measurement time. To put this in perspective, this force is equivalent to the gravitational pull between two people at a distance of approximately 100 km. This high sensitivity confirms that the mechanical resonators are in thermal equilibrium with their environment and not suffering from any spurious heating or vibrations that would be detrimental for force sensing.
Together, these two complementary studies show great promise for future experiments. The fabrication and measurement techniques demonstrated here are relevant to practical sensing applications beyond mere force sensing. These applications include, for example, accelerometry and magnetometry [10]. Likewise, future quantum experiments [6] can exploit the exquisite properties of these devices. One could imagine integrating trampoline resonators as one node of a large hybrid quantum network, or even verifying the quantum nature of macroscopic mechanical motion by observing an individual quantum jump in the number of mechanical excitations.
This research is published in Physical Review Letters and Physical Review X.
References
- R. A. Norte, J. P. Moura, and S. Gröblacher, “Mechanical Resonators for Quantum Optomechanics Experiments at Room Temperature,” Phys. Rev. Lett. 116, 147202 (2016).
- C. Reinhardt, T. Müller, A. Bourassa, and J. C. Sankey, “Ultralow-Noise SiN Trampoline Resonators for Sensing and Optomechanics,” Phys. Rev. X 6, 021001 (2016).
- D. Rugar, R. Budakian, H. J. Mamin, and B. W. Chui, “Single Spin Detection by Magnetic Resonance Force Microscopy,” Nature 430, 329 (2004).
- B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Observation of Gravitational Waves from a Binary Black Hole Merger,” Phys. Rev. Lett. 116, 061102 (2016).
- D. Leibfried, R. Blatt, C. Monroe, and D. Wineland, “Quantum Dynamics of Single Trapped Ions,” Rev. Mod. Phys. 75, 281 (2003).
- M. Aspelmeyer, T. J. Kippenberg, and F. Marquardt, “Cavity Optomechanics,” Rev. Mod. Phys. 86, 1391 (2014).
- J. D. Teufel, T. Donner, D. Li, J. W. Harlow, M. S. Allman, K. Cicak, A. J. Sirois, J. D. Whittaker, K. W. Lehnert, and R. W. Simmonds, “Sideband Cooling of Micromechanical Motion to the Quantum Ground State,” Nature 475, 359 (2011).
- J. Chan, T. P. M. Alegre, A. H. Safavi-Naeini, J. T. Hill, A. Krause, S. Gröblacher, M. Aspelmeyer, and O. Painter, “Laser Cooling of a Nanomechanical Oscillator into its Quantum Ground State,” Nature 478, 89 (2011).
- J. D. Thompson, B. M. Zwickl, A. M. Jayich, F. Marquardt, S. M. Girvin, and J. G. E. Harris, “Strong Dispersive Coupling of a High-Finesse Cavity to a Micromechanical Membrane,” Nature 452, 72 (2008).
- M. Metcalfe, “Applications of Cavity Optomechanics,” Appl. Phys. Rev. 1, 031105 (2014).