Squeezed Light Reengineers Resonance Fluorescence

Howard J. Carmichael

Viewpoint

Squeezed Light Reengineers Resonance Fluorescence

The Dodd-Walls Centre for Photonic and Quantum Technologies, Department of Physics, University of Auckland, Private Bag 92019, Auckland, New Zealand

July 11, 2016• Physics 9, 77

By bathing a superconducting qubit in squeezed light, researchers have been able to confirm a decades-old prediction for the resulting phase-dependent spectrum of resonance fluorescence.

Figure caption — **Figure 1:** The spectrum of quasielastic scattering in resonance fluorescence: (a) the Mollow spectrum [3] for a two-state system in a bath of ordinary vacuum fluctuations (red circle). (b, c) modified spectra [6] for a two-state system in a bath of vacuum fluctuations that have been squeezed (blue ellipses). The degree of squeezing corresponds to a number of photons per bath radiation mode of $N = 0.12$ . The red circle and blue ellipses represent the amplitude of radiation field fluctuations, where fluctuations aligned with the light blue arrow are in phase with the coherent drive, while those at right angles are $𝜋 ∕ 2$ out of phase. Natural linewidth is the linewith of spontaneous emission from the system in ordinary vacuum.

Resonance fluorescence is an iconic example of quantum optics in open systems—those that interact with the environment. It describes the scattering of light from a two-state system, such as an atom, that is illuminated by light at its resonance frequency, and it is a direct result of quantum fluctuations in the vacuum. In a remarkable experiment with a superconducting-circuit qubit and squeezed microwave photons, researchers have extended the observation of resonance fluorescence from a two-state system bathed by ordinary vacuum fluctuations to one embedded in a reengineered bath where vacuum fluctuations are squeezed, thus permitting narrow spectroscopic lines to be observed [1]. This work, from the laboratory of Irfan Siddiqi at the University of California, Berkeley, realizes a theoretical proposal of some 30 years standing, and it demonstrates, yet again, the power of superconducting-circuit quantum optics in addressing textbook physics in the area of simple open quantum systems.

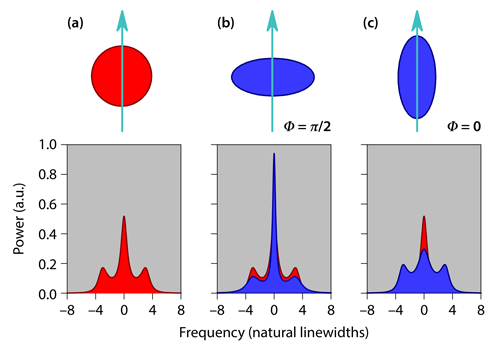
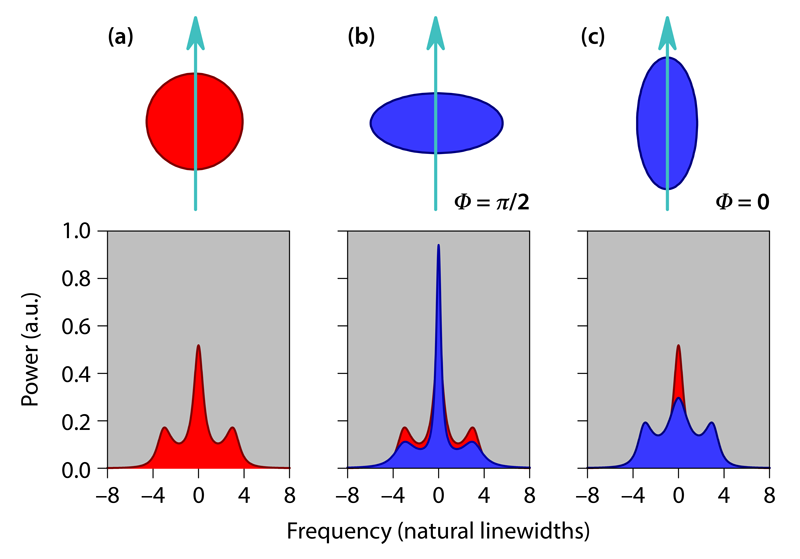
From the late 1960s to the early 1970s, the spectrum of resonance fluorescence was widely discussed as a potential target of the recently invented laser; what might it reveal about the quantum versus the semiclassical theory of light? Its measurement by laser excitation of sodium atoms [2] was reported in 1974. At the time, the precise form of the spectrum was still under debate. Soon, however, the following picture emerged: First, a two-state system excited on resonance by a laser (a coherent drive) scatters both elastic photons—which have the same frequency as the drive—and quasielastic photons. Second, as the drive strength increases, quasielastic scattering dominates and the spectrum takes the form of the so-called Mollow triplet [3] (Fig. 1)—a central peak at the frequency of the drive plus symmetrically placed sidebands, which arise from an effect known as Rabi flopping. Third, the central-peak linewidth is the inverse spontaneous lifetime of the system’s excited state (the natural width), while the sidebands are broader by a factor of 3/2.

The Mollow spectrum of resonance fluorescence, measured first for atoms, has been carried forward as a figure of merit for the coherent manipulation of both semiconductor nanocrystals (quantum dots) and superconducting-circuit qubits [4]. The spectrum describes the photon emission into a bath that is in the vacuum state and contains no photons. Photon emission into a bath that already contains photons is a sum of spontaneous emission and stimulated emission. In a thermal bath with an average $N$ photons per mode of the bath radiation field, the total emission rate is the spontaneous emission rate multiplied by $N + 1$ , where the $N$ represents the additional stimulated emission. A bath with the vacuum fluctuations squeezed also contains $N$ photons per mode, with $N$ set by the degree of squeezing. Unlike in a thermal bath, however, photons in this reengineered bath are created as correlated pairs, with the frequencies of each pair symmetrically placed around a reference frequency—the resonance frequency of the two-state system. In this case, the vacuum fluctuations have undergone phase-sensitive amplification and deamplification to produce the $N$ photons per mode (see Fig. 1), and the phase sensitivity dramatically changes bath-induced radiative decay rates and the spectrum of resonance fluorescence.

The quasielastic scattering of resonance fluorescence may be viewed as emission from an electric dipole under the influence of a coherent drive plus bath fluctuations. In the reengineered bath, fluctuations of phase $Φ$ relative to the drive are amplified, while those of phase $Φ + 𝜋 ∕ 2$ are deamplified. Bath fluctuations translate into radiative decay rates, and therefore, a dipole embedded in fluctuations that are squeezed exhibits phase-sensitive decay and resonance fluorescence (see Fig. 1). In particular, the central peak of the Mollow spectrum can be made sharper, achieving a smaller width than is set by ordinary vacuum fluctuations.

Phase-dependent dipole decay was proposed theoretically by Crispin Gardiner in 1986 [5] and seen in an experiment with a superconducting artificial atom for the first time in 2013 [6]. The implications for the spectrum of resonance fluorescence were worked out soon after Gardiner’s proposal [7]. At the time, the only credible two-state system was an atom, for which the experimental challenges were, and still are, formidable. Observing the spectrum of resonance fluorescence of an atom in a squeezed vacuum requires meeting several challenges: all spatial modes of the bath radiation field coupled to the atom must be squeezed; the bandwidth of the squeezing (the range of frequencies squeezed) must span the fluorescence spectrum; the phase of the squeeze operation relative to the drive must be controlled; and photon loss, as always, is detrimental to the delivery of squeezed radiation and must be minimized. Siddiqi and colleagues overcome all such obstacles in their experiment.

The authors realize a two-state system by strongly coupling a superconducting qubit to a microwave waveguide. Strong coupling between the qubit and the cavity results in a polariton resonance, whereby the system undergoes a transition from the ground state (qubit unexcited and no microwave photon in the cavity) to one of two hybridized first-excited states (qubit excited or one photon in the cavity in an equally weighted quantum superposition). The photon blockade effect, in which the absorption of a first photon by the cavity “blocks” the absorption of a second, allows higher excited states (more photons in the cavity) to be ignored; in effect, the hybridized qubit-cavity system behaves as a two-state system [8]. One advantage of this configuration is that the cavity provides a strongly coupled port for efficient injection of microwave squeezed radiation [9] and a separate, weakly coupled, port for the coherent drive. Most of the system’s fluorescence exits the cavity through the strongly coupled port where it combines with reflected squeezed radiation prior to detection. A device called a Josephson parametric amplifier generates the squeezed radiation. To realize the photon blockade effect, the bandwidth of the radiation is designed to be small enough that the transition from the first to the second excited state remains far from resonance; the bandwidth is also much larger than the width of the polariton resonance, in order that the fluorescence spectrum is spanned. Another Josephson parametric amplifier of near-quantum-limited noise performance avoids contamination by noise beyond the minimum that quantum mechanics requires and permits direct fluorescence measurements with a microwave spectrum analyzer. At the operating temperature of 30 mK, the thermal photon number is less than 0.01, which is smaller than the photon number generated by the injected squeezed radiation by about a factor of 10, and therefore a minimal contamination.

Coupling of the two-state system to unsqueezed vacuum modes degrades the presented squeezing by a factor of 0.81, while degradation due to photon loss reduces the overall efficiency of the experiment to 0.55. Despite these imperfections, the measured fluorescence spectra are remarkably similar to those plotted in Fig. 1. After fitting their spectra to theoretical predictions, the authors recover linewidths that depend on the phase of the drive relative to the phase of the vacuum squeezing in the expected way; in particular, a linewidth reduced by 3.1 dB below the width due to ordinary vacuum fluctuations is observed for an in-phase drive. The researchers provide long-awaited verification of textbook theory, while at the same time showcasing the stunning advances of microwave quantum optics—quantum optics with the tiniest of quanta, each just 30 $𝜇$ eV. They have opened a path to new ways of characterizing squeezed radiation sources and a path to the further study of atoms in interaction with squeezed radiation [10], including radiation generated internally by the atom itself rather than by an external source [11].

This research is published in Physical Review X.

References

D. M. Toyli, A. W. Eddins, S. Boutin, S. Puri, D. Hover, V. Bolkhovsky, W. D. Oliver, A. Blais, and I. Siddiqi, “Resonance Fluorescence from an Artificial Atom in Squeezed Vacuum,” Phys. Rev. X 6, 031004 (2016).
S. Schuda, C. R. Stroud Jr., and M. Hercher, “Observation of the Resonant Stark Effect at Optical Frequencies,” J. Phys. B 7, L198 (1974).
B. R. Mollow, “Power Spectrum of Light Scattered by Two-Level Systems,” Phys. Rev. 188, 1969 (1969).
A. Muller, E. B. Flagg, P. Bianucci, X. Y. Wang, D. G. Deppe, W. Ma, J. Zhang, G. J. Salamo, M. Xiao, and C. K. Shih, “Resonance Fluorescence from a Coherently Driven Semiconductor Quantum Dot in a Cavity,” Phys. Rev. Lett. 99, 187402 (2007); X. Xu, B. Sun, P. R. Berman, D. G. Steel, A. S. Bracker, D. Gammon, and L. J. Sham, “Coherent Optical Spectroscopy of a Strongly Driven Quantum Dot,” Science 317, 929 (2007); O. Astafiev, A. M. Zagoskin, A. A. Abdumalikov, Yu. A. Pashkin, T. Yamamoto, K. Inomata, Y. Nakamura, and J. S. Tsai, “Resonance Fluorescence of a Single Artificial Atom,” Science 327, 840 (2010).
C. W. Gardiner, “Inhibition of Atomic Phase Decays by Squeezed Light: A Direct Effect of Squeezing,” Phys. Rev. Lett. 56, 1917 (1986).
K. W. Murch, S. J. Weber, K. M. Beck, E. Ginossar, and I. Siddiqi, “Reduction of the Radiative Decay of Atomic Coherence in Squeezed Vacuum,” Nature 499, 62 (2013).
H. J. Carmichael, A. S. Lane, and D. F. Walls, “Resonance Fluorescence from an Atom in a Squeezed Vacuum,” Phys. Rev. Lett. 58, 2539 (1987); H.J. Carmichael, A.S. Lane, and D.F. Walls, “Resonance Fluorescence in a Squeezed Vacuum,” J. Mod. Opt. 34, 821 (1987).
L. Tian and H. J. Carmichael, “Quantum Trajectory Simulations of Two-State Behavior in an Optical Cavity Containing One Atom,” Phys. Rev. A 46, R6801 (1992); C. Lang, D. Bozyigit, E. Eichler, L. Steffen, J. M. Fink, A. A. Abdumalikov, M. Baur, S. Filip, P. A. da Silva, A. Blais, and A. Wallraff, “Observation of Resonant Photon Blockade at Microwave Frequencies Using Correlation Function Measurements,” Phys. Rev. Lett. 106, 243601 (2011).
A. S. Parkins, P. Zoller, and H. J. Carmichael, “Spectral Linewidth Narrowing in a Strongly Coupled Atom-Cavity System Via Squeezed-Light Excitation of a ‘‘Vacuum’’ Rabi Resonance,” Phys. Rev. A 48, 758 (1993).
B. J. Dalton, Z. Ficek, and S. Swain, “Atoms in Squeezed Light Fields,” J. Mod. Opt. 46, 379 (1999).
P. R. Rice and H. J. Carmichael, “Nonclassical Effects in Optical Spectra,” J. .Opt. Soc. Am. B 5, 1661 (1988); H. J. Carmichael, R. J. Brecha, M. G. Raizen, H. J. Kimble, and P. R. Rice, “Subnatural Linewidth Averaging for Coupled Atomic and Cavity-Mode Oscillators,” Phys. Rev. A 40, 5516 (1989).

About the Author

Howard Carmichael is the Dan Walls Chair of Theoretical Physics at the University of Auckland. He worked for many years in the United States, first at the University of Arkansas, Fayetteville, and then at the University of Oregon, Eugene, where he was Associate Professor then Professor from 1989 to 2002. His research specialty is quantum optics and the theory of open quantum systems. He is the originator of Quantum Trajectory Theory. In 2015 he was recognized as an Outstanding Referee by the American Physical Society.