New Wrinkle On Fighting Crow’s Feet
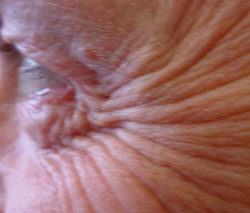
What do plastic garbage bags, human flesh, and the skins of apples all have in common? Wrinkles. Classical theory can predict where wrinkles will occur, but their amplitude and wavelength–and the best chance to eliminate them–has proven more difficult. Now, in the 21 February print issue of PRL, a team discovers a general law that quantitatively predicts the size, shape, and structure of wrinkles that appear on any thin film. As simple examples, they correctly estimate the wavelengths for wrinkles on a dried-up apple and on the squeezed skin of a hand. The theory could potentially be used in the manufacture of defect-free thin sheets of paper, glass, metal, and silicon chips. It may even help to control the “crow’s feet” wrinkles that appear around people’s eyes as they age.
Enrique Cerda and L. Mahadevan of the University of Cambridge in England realized that many wrinkling systems could be analyzed in a single theoretical framework in which a thin sheet is attached to a thick but not completely rigid foundation. The skin of a dried apple wrinkles because it’s attached to the flesh, which has shrunk from drying. The skin’s surface area must remain constant while accommodating a reduced apple diameter. But how does it choose the wavelength?
Cerda and Mahadevan’s theory explains that the wavelength is a compromise between the competing interests of the skin and the flesh. A thin sheet always prefers one large wave to many small ripples, which store more energy. (Just imagine trying to keep a ribbon compressed into many tight S-turns rather than a single loop.) The foundation, on the other hand, is relatively stiff and prefers the smallest waves possible. The team’s theory predicts the wavelength and other properties that result from this competition. For a stretched rubber sheet with no foundation, the theory defines an “effective” foundation–the tension in the sheet, which favors smaller wavelengths, just as a real foundation does.
As a first test of their theory, Cerda and Mahadevan make rough estimates for the wrinkling wavelengths for a dried apple and squeezed skin on the back of a hand. Using the material properties of apples and skin, the theory suggests wavelengths of about 1.5 mm and 2.5 mm, which are not far from their observations. They published a more quantitative test for the case of a rubber sheet in a separate paper [1] but did not present the theory there.
Once researchers can predict the placement, height, and wavelength of wrinkles, they can take steps to prevent them. For example, some of the crow’s foot wrinkles around an eye could be eliminated by causing a few, carefully selected spots nearby to swell (perhaps with an ointment), which would pull the skin taut and flatten out the wrinkle. For so-called compression wrinkles, Mahadevan suggests paralyzing the proper muscles, just as the popular cosmetic treatment Botox does.
Robert Kohn of New York University is impressed by the team’s work. “This paper is truly the first of its type. The authors’ accomplishment is much greater than the casual reader might realize,” he says. “This work on wrinkling will make its way into textbooks as an informative example showing how energy minimization can induce pattern formation.”
–Dan Drollette Jr.
Dan Drollette is a freelance science writer in Northampton, MA.
References
- E. Cerda, K. Ravi-Chandar, and L. Mahadevan, Nature (London) 419, 579 (2002)


