Light Beam with a Curve
A new optics experiment makes a light beam appear to bend in air. The brightest patch of the beam also appears to travel with almost no spreading, unlike ordinary laser beams, as a team reports in the 23 November Physical Review Letters. The so-called Airy beam may lead to new kinds of optical engineering.
Any ordinary beam of light spreads as it travels, thanks to the wave effect known as diffraction. Even a laser pointer’s beam gets wider and dimmer on the way to a distant screen. But in 1987 a team introduced the Bessel beam, whose intensity remains constant as you move away from the source [1]. The “trick” is that light doesn’t actually travel along the beam axis; the intensity at any location in the beam results from the complicated interference of light emerging from all points in a large, ring-shaped slit at the source. Other researchers have devised variations on the Bessel beam that have other surprising properties.
Now Demetri Christodoulides, Aristide Dogariu, and their colleagues at the University of Central Florida in Orlando have come up with a new family of non-diffracting waveforms that have another, even stranger property: they appear to curve. The Airy waveform was described theoretically nearly 30 years ago as a surprising solution to the quantum equation for a free particle, a problem with a mathematical analogy in optics [2].
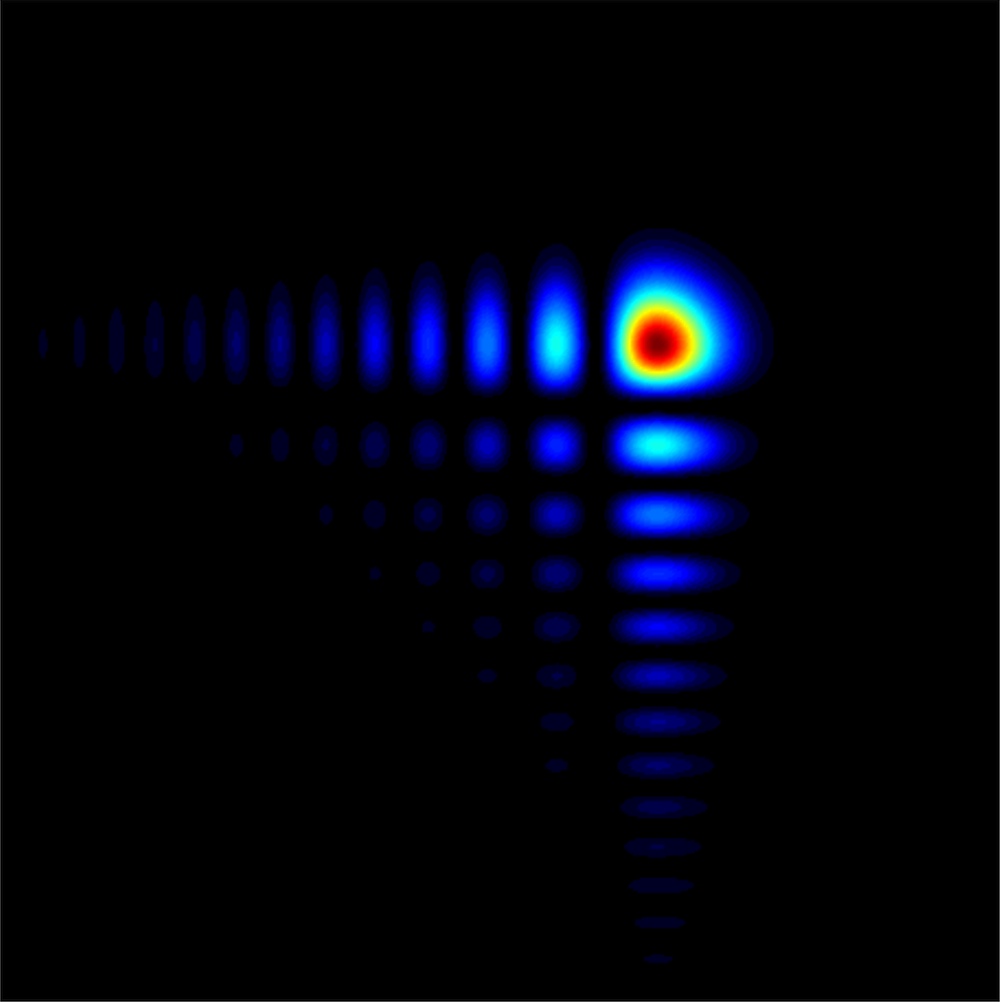
The beam is asymmetric, with one bright region at the center and a series of progressively dimmer patches on one side of the central spot. But rather than propagating in a straight line, the entire pattern of bright and dark patches curves toward one side. At the same time, the width and intensity of each patch remains essentially constant, even after an ordinary beam would have dropped to nearly half its original intensity and spread to several times its original width.
The repeated dim patches of an ideal Airy beam extend sideways to infinity, but Christodoulides and his colleagues recently realized that they could approximate it fairly well using an ordinary laser [3]. The bell-shaped beam profile happens to correspond well mathematically with a “truncated” Airy wave.
To make the beam, the researchers directed a centimeter-wide laser beam onto a watch-sized liquid crystal display screen called a spatial light modulator (SLM). The reflectivity of each pixel on this screen is related to its index of refraction, so the device allows control of the precise phase of light reflected from each spot. The team programmed the SLM pixels to provide the phase relationships needed for an Airy beam.
Their measurements of the beam’s profile at several locations agreed with theoretical predictions, including the beam’s bending and lack of spreading. Next the team reprogrammed the SLM to generate a two-dimensional Airy beam–one with secondary spots both below and to the left of the main spot. It curved up and to the right.
As with the Bessel beam’s diffraction-free “propagation,” light doesn’t actually propagate along the curved path. The beam is the pattern created by interference of light from the 500,000 carefully-phased pixels of the SLM. Still, Mordechai Segev of the Israel Institute of Technology in Haifa is impressed. “It’s a beautiful piece of work,” he says. Segev envisions using similar phasing tricks in situations where multiple light beams are needed to create a specific light effect at a precise distance from the source. “If you engineer the phase the right way, you will only have white light where the pulses meet. Imagine if you did something like that in the atmosphere,” where Airy-like beams could improve LIDAR, a type of laser-based radar used to study the atmosphere.
–Mike Wofsey
References
- J. Durnin, J. J. Miceli, and J. H. Eberly, “Diffraction-Free Beams,” Phys. Rev. Lett. 58, 1499 (1987)
- M. V. Berry and N. L. Balazs, “Nonspreading Wave Packets,” Am. J. Phys. 47, 264 (1979)
- G. A. Siviloglou and D. N. Christodoulides, “Accelerating Finite Energy Airy Beams,” Opt. Lett. 32, 979 (2007)
More Information
Focus story related to Bessel beams from 2003 Airy rainbow simulator Airy functions and tsunamis: M. V. Berry, “Tsunami Asymptotics,” New J. Phys. 7, 129 (2005)