Elizabethan Geometry
The complicated shape of a warped leaf or a human ear can emerge from surprisingly simple rules–cells grow in the right places and create the right stresses. In the 8 August and 10 October issues of Physical Review Letters, researchers mathematically analyze how a growing disc can take on any shape from a cone to a potato chip to a ruffled Elizabethan collar. The results expand the understanding of the rich palette of spontaneously-forming shapes in nature.
If you cut out a wedge from a circle of stiff paper and tape the two cut edges together, you get a cone. Julien Dervaux and Martine Ben Amar of the École Normale Supérieure (ENS) in Paris describe in their August paper how something similar happens when a thin, circular membrane expands in a non-uniform way, for example, in a growing plant. Others have looked at a disk with a growth rate that varies from the center to the edge and that grows equally in all directions. But Dervaux and Ben Amar analyze the case where the circumference and the radius grow at different rates. If the outward, radial growth is faster, the outside edge isn’t long enough to go around the flat disk, so it distorts into a cone.
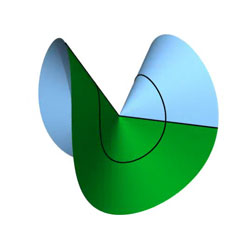
But if the outward growth is slower than the circumference growth, the outside edge becomes too long instead of too short. The same effect occurs in the paper cutout if you tape in a larger wedge than you removed, the extra amount measured by what the team calls the excess angle. Using a mathematical analysis–as well as actual paper cutouts–the researchers show that the membrane naturally buckles to form a shape reminiscent of a saddle. But unlike a saddle, if you sliced this shape along the diameter, you would see perfectly straight edges in the cross section. Like a cone, it’s curved in the “circumferential” direction but straight in the radial direction. The team suggests that this shape is similar to that of Acetabularia acetabulum, an algae that also forms a cone and a flat disk, during different phases of its growth.
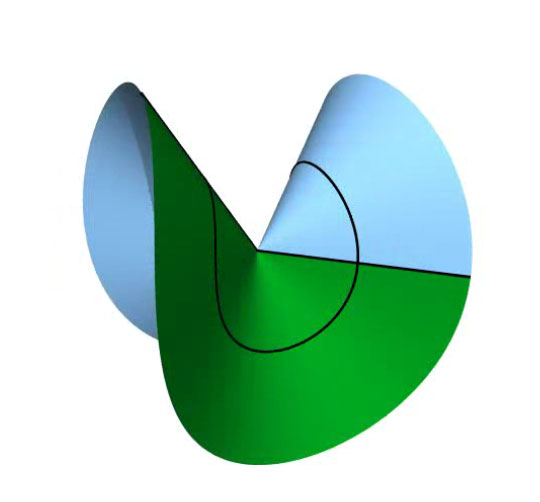
Martin Michael Müller, now at ENS, and Jemal Guven of the National Autonomous University of Mexico (UNAM) in Mexico City have previously described ordinary cones using differential geometry techniques more commonly employed for curved spacetime. While Dervaux and Ben Amar’s August paper considers the tiny deviations from flatness that result from inserting a sliver of extra material in the disk, Müller and Guven’s October paper with Ben Amar applies these mathematical tools to shapes with large excess angles. The team found that there are infinitely many ways to warp the disk, each corresponding to a different number of undulations around the perimeter.
The twofold buckling, with two upward and two downward bends, requires the least energy. But as the excess angle increases, neighboring undulations eventually bump into each other. “At that point, where it starts to touch, the threefold becomes important,” says Müller. If the excess grows larger still, new shapes with four, five or more undulations successively take over, eventually resembling the “ruff” collars seen in Elizabethan portraits. Finally, for excess angles larger than about 2000 degrees, no undulating shape can accommodate the excess without bumping into itself.
Thomas Witten of the University of Chicago calls the new results a “pretty piece of math.” He says “examples of this kind of buckling are well appreciated and known,” but “the richness of this buckling has only recently been appreciated.”
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.
More Information
Past Focus stories involving mechanical forces in plants: String Theory for Plants Cactus Patterns Buckle Up