Why Leaves Aren’t Trees
Supply networks, such as the blood vessels that bring nutrients to our cells, often show tree-like branching into ever-finer channels. Three papers in the 29 January Physical Review Letters explore the effects of different conditions on the size and structure of such networks. One paper argues that blood networks evolve to keep their volume as small as possible. Two other papers independently report that vein networks in leaves include loops in their structures in order to better respond to damage or variability in nutrient demand. The results are relevant not only to biology but also to constructed networks that distribute goods over roads or electrical power over wires.
Bigger creatures use less energy, relative to their mass, than smaller ones do, so a human’s heart beats more slowly than a mouse’s. One explanation is that keeping warm is the essential factor, and body heat escapes through the animal’s outer surface. The surface area is proportional to the square of the animal’s linear size, while the mass is proportional to its cube, just as for a uniform sphere. A little manipulation of these facts suggests that the total energy use should grow in proportion to the mass to the power 2/3, or (D-1)/D, where the dimension D is 3. But for decades the data have suggested a power of 3/4. An influential 1997 paper attributed this exponent to the highly branched “fractal” geometry of the circulatory system, which makes it equivalent to four dimensional, so that (D-1)/D = 3/4 [1].
Peter Dodds of the University of Vermont in Burlington questions both the experimental and theoretical basis for this claim. In 2001, he and his colleagues analyzed data on mammals and birds and concluded that they were consistent with the original exponent of 2/3 [2]. He and others have also criticized the theoretical basis of the fractal analysis. Now Dodds has devised a theoretical argument for the lower value of 2/3, based on the geometry of the circulatory network.
“This is the most stripped-down version of the network story that held water,” Dodds says. His new theory chooses the network geometry that uses the smallest possible volume of blood, rather than the minimum amount of energy to pump it around the body. Even in a highly branched network, he calculates a 2/3 exponent, supporting his view of the experimental data, and also agreeing with the surface area argument. Dodds’s model also successfully accounts for the data on river basin networks.
Jayanth Banavar of Pennsylvania State University in University Park and Amos Maritan of the University of Padova, Italy, aren’t convinced. If you look at data over a wide range of body masses–from micro-organisms to the largest animals–and compare the accuracy of the 2/3 formula with the 3/4 formula, “you will see the difference,” Maritan says. Banavar agrees with Dodds that the fractal geometry “was truly not the essential reason for the 3/4” but believes this exponent is correct and arises for other reasons. “The controversy goes on,” he concludes.
Other researchers are looking at the structures of networks. A decade ago, Banavar, Maritan, and others showed that branching appears whenever there are economies of scale, so that combining two channels into a larger one reduces the “cost.” They proved that the optimal branched networks are always mathematical trees, which contain no loops.
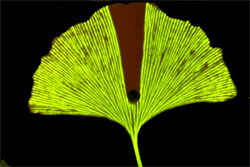
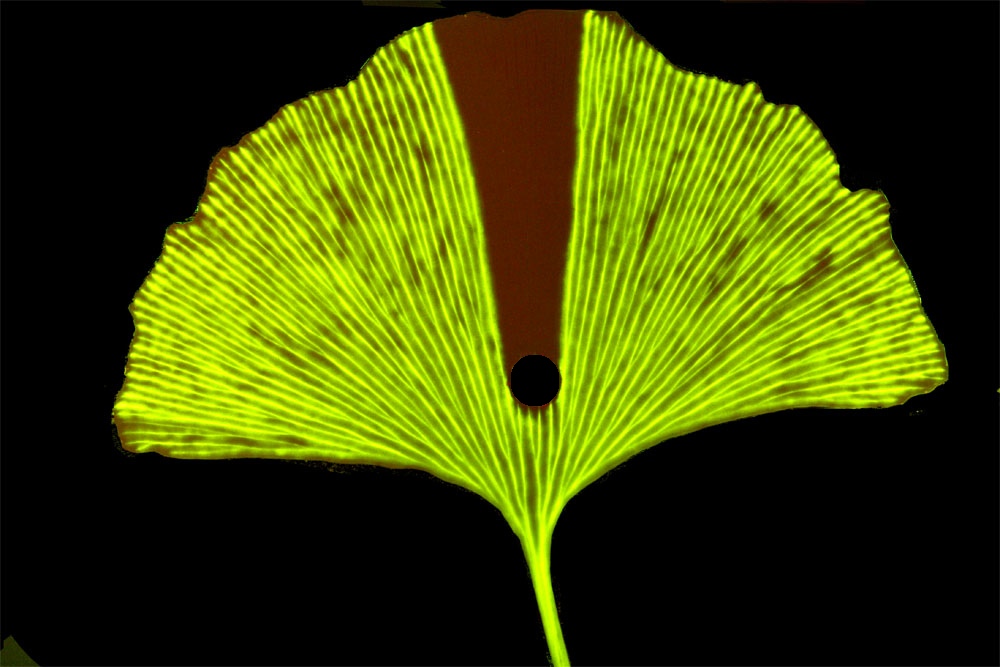
But real leaves often do have loops. To understand why, Francis Corson, who recently moved from the École Normale Supérieure in Paris to Rockefeller University in New York City, explored a model that included a demand for nutrients that wasn’t fixed but varied in time. In spite of the extensive literature, “people hadn’t really examined in detail the effect of fluctuations” says Corson. On a computer, Corson generated random networks and calculated the fluid flow as the demand varied. He then tweaked the sizes of the channels to find the arrangement that used the least energy to drive the flow. When the advantage of consolidating channels was modest, the best networks had loops, because the fluid could follow different paths as conditions changed.
A group led by Marcelo Magnasco of Rockefeller, independently found the same thing. In addition, the simulations favored loops as a way of rerouting nutrients in response to damage to the network, as confirmed in experiments with dyes in real leaves. Team member Eleni Katifori cautions that there is much more to learn about the variety of structures of leaf vein networks. “Biology is extremely complicated, and for every rule there are hundreds of exceptions.”
The two papers “put a new ingredient in this interesting problem” by considering how networks deal with changing demands, Maritan says. “They are showing that this leads to loops, but this story is only the beginning.”
–Don Monroe
Don Monroe is a freelance science writer in Murray Hill, New Jersey.
References
- G. B. West, J. H. Brown, and B. J. Enquist, “A General Model for the Origin of Allometric Scaling Laws in Biology,” Science 276, 122 (1997)
- P. S. Dodds, D. H. Rothman, and J. S. Weitz, “Re-examination of the ‘3/4-law’ of Metabolism,” J. Theor. Biol. 209, 9 (2001)