Rod-Shaped Nucleus
We picture atomic nuclei as spherical globs of protons and neutrons, although they can also be egg-shaped. Now calculations published 9 September in Physical Review Letters show that an even more exotic shape is possible: a rapidly spinning nucleus can form into a linear chain of several small clusters of neutrons and protons. Such exotic nuclear states could play important intermediary roles in the formation of carbon-12 and oxygen-16–elements essential for life–in the interiors of stars. The authors’ new technique for calculating such structures also allows for the study of even more exotic arrangements.
The shape of a nucleus has important effects on nuclear reactions, such as those in stars, where almost all of the natural elements are generated. If a nucleus is spinning rapidly enough–usually the result of an off-center collision-and-fusing of two smaller nuclei–its shape can become deformed from the usual sphere or ellipsoid. This shape stems from the interplay between the attractive strong force holding the protons and neutrons together (collectively “nucleons”) and the centrifugal force pulling them apart. Experiments have provided evidence for such highly deformed nuclei with width-to-length ratios of 1-to-2 or 1-to-3 in heavy elements. For light nuclei, however, such as carbon and oxygen, there have been indications that highly deformed states might exist, but no clear evidence, despite intensive experimental searches.
Rather than working at the level of individual nucleons, most theoretical calculations in this field have treated the nucleus as composed of alpha particles–tightly bound groups of two protons and two neutrons. Using alpha particles is often a good approximation, necessary to reduce the computational requirements of the calculations. However, theorists feel that a more satisfactory understanding should treat the individual nucleons as the fundamental building blocks, with the clusters and their properties emerging from the calculations.
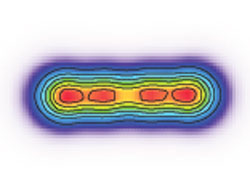
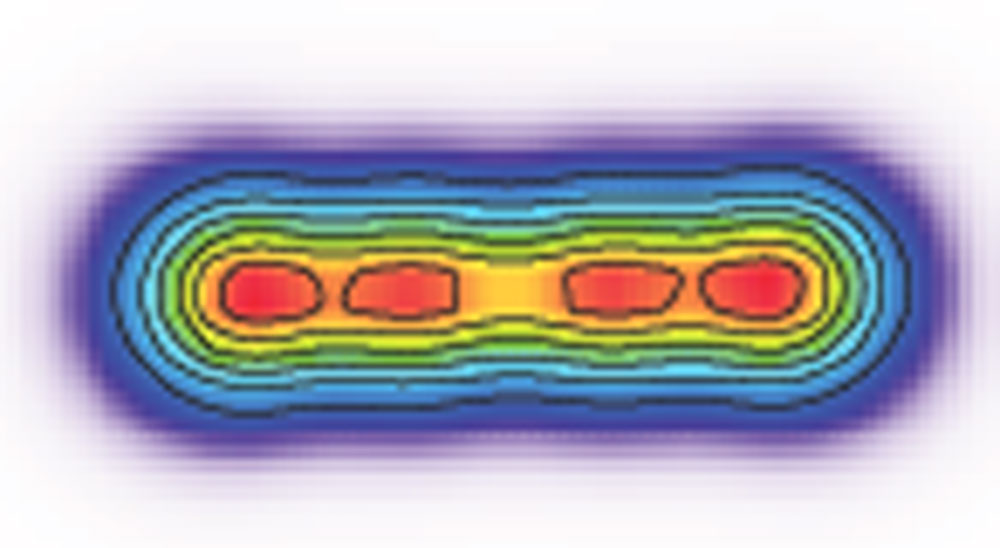
Takatoshi Ichikawa of Kyoto University and his colleagues have now taken this more fundamental approach by combining some recent improvements in the techniques. The team used a technique known as the Hartree-Fock method to study a rotating oxygen-16 nucleus. They described interactions between the nucleons in terms of so-called Skyrme forces, approximations for the strong force, the force that binds nucleons together. The team generated a three-dimensional nucleon density distribution that showed the nucleus’s shape.
At rotational frequencies less than 1.5 mega-electron-volts/h-bar (MeV/h-bar, where h-bar is Planck’s constant divided by 2π), the nucleus remains spherical, according to the calculations. However, at frequencies around 2.0 MeV/h-bar, the nucleus stably settles into a configuration of four alpha particles arranged along a line. If the nucleus rotates much faster than this, it breaks apart. The linear “chain” structure has never been demonstrated as stable in a calculation for a nucleus of any size, although theorists have previously suggested that it might exist. Further calculations by the team showed that this new state could appear when an oxygen-16 nucleus forms from the collision of two beryllium-8 nuclei in experiments or inside a star.
Sait Umar of Vanderbilt University thinks that such linear-chain configurations are “of fundamental importance to the structure and dynamics of these systems” They could also be important in the creation of carbon-12 and oxygen-16 from collisions of smaller nuclei inside stars, he says. In future work, the team hopes to use their technique to look for longer linear chains and perhaps even polygons.
–Michelangelo D'Agostino
Michelangelo D’Agostino is a physicist and freelance science writer in Berkeley, California.