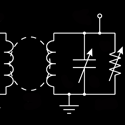
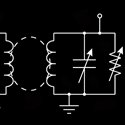
Circuit Analysis
Everyone learns in a first course on quantum mechanics that the result of a measurement cannot be a complex number, so the quantum mechanical operator that corresponds to a measurement must be Hermitian. However, certain classes of complex Hamiltonians that are not Hermitian can still have real eigenvalues. The key property of these Hamiltonians is that they are parity-time (PT) symmetric, that is, they are invariant under a mirror reflection and complex conjugation (which is equivalent to time reversal).
Hamiltonians that have PT symmetry have been used to describe the depinning of vortex flux lines in type-II superconductors and optical effects that involve a complex index of refraction, but there has never been a simple physical system where the effects of PT symmetry can be clearly understood and explored. Now, Joseph Schindler and colleagues at Wesleyan University in Connecticut have devised a simple LRC electrical circuit that displays directly the effects of PT symmetry. The key components are a pair of coupled resonant circuits, one with active gain and the other with an equivalent amount of loss. Schindler et al. explore the eigenfrequencies of this system as a function of the “gain/loss” parameter that controls the degree of amplification and attenuation of the system. For a critical value of this parameter, the eigenfrequencies undergo a spontaneous phase transition from real to complex values, while the eigenstates coalesce and acquire a definite chirality (handedness). This simple electronic analog to a quantum Hamiltonian could be a useful reference point for studying more complex applications. – Gordon W. F. Drake