Superposed in a Crystal
In quantum mechanics, a system with distinct eigenstates can exist in a superposition of two or more states with specific probability amplitudes. The creation and manipulation of these superpositions is central to quantum computing. Efforts to experimentally realize quantum superpositions of macroscopic objects that are larger than an electron or a photon have generally focused on controlling their quantum dynamics and their interaction with the environment. Strings of trapped ions, an interesting example of many-body objects that can behave quantum mechanically, have attracted attention due to their remarkable contribution to quantum technologies, such as their use in the realization of quantum simulators and quantum teleportation protocols.
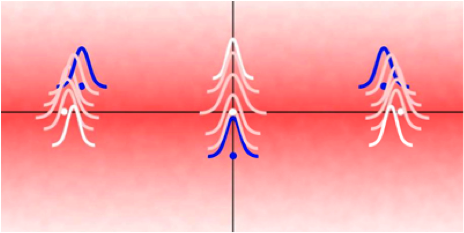
In an article in Physical Review A, Jens Baltrusch at Saarland University, Germany, and his colleagues report theoretical work on the dynamics of two different structures—linear and zigzag—of a trapped ion crystal. Starting out with a chain of ions at rest in a regime close to its structural phase transition, they excite—with spin-dependent trapping—a particular ion of the crystal into a superposition of metastable electronic states. Coulomb forces then modify the motions of the other ions in relation to the state of the chosen one, producing a state in which all the ions are entangled. This state is manifested as a superposition of different crystalline structures—a so-called cat state—and, according to the authors, should be observable with interferometry. – Jihane Mimih